高中数学人教A版 (2019)选择性必修 第一册2.5 直线与圆、圆与圆的位置教课ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册2.5 直线与圆、圆与圆的位置教课ppt课件，共18页。PPT课件主要包含了d＝r，Δ＝0，∴EF平分CD，答案2066等内容，欢迎下载使用。

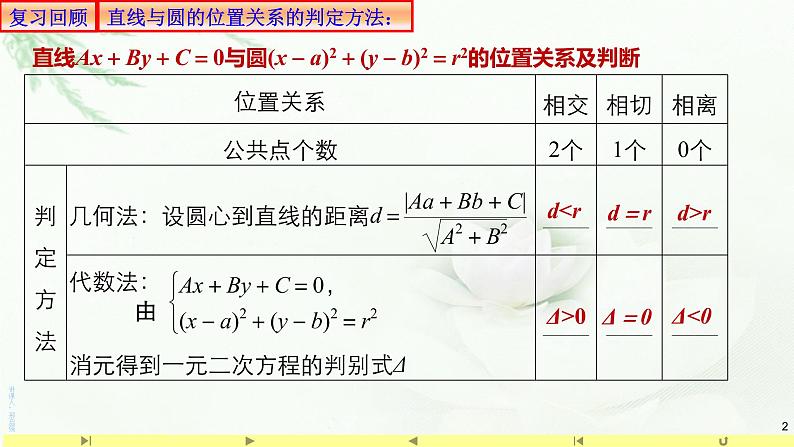
直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系及判断
直线与圆的位置关系的判定方法：
切线方程的求法1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可通过数形结合求出.
求直线与圆相交时弦长的两种方法(1)几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,圆的半
例1.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑，求支柱A2P2的高度（精确到0.01m).
分析：建立如图所示的直角坐标系，要得到支柱A2P2的高度，只需求出点P2的纵坐标.
解：建立如图所示的直角坐标系，使线段AB所在直线为x轴，O为坐标原点，圆心在y轴上，由题意，点P,B的坐标分别为（0,4),(10,0),设圆心坐标是(0,b),圆的半径是r，那么圆的方程是x2＋(y－b)2＝r2 .
思考:如果不建立平面直角坐标系，你能解决这个问题吗？由此比较综合法和坐标法的特点。
某圆拱桥的水面跨度20m，拱高4m.现有一船，宽10m，水面以上高3m，这条船能否从桥下通过？
解　建立如图所示的坐标系.
依题意,有A(－10,0),B(10,0),P(0,4),D(－5,0)，E(5,0).设所求圆的方程是(x－a)2＋(y－b)2＝r2，
解此方程组，得a＝0，b＝－10.5，r＝14.5.
所以这座圆拱桥的拱圆的方程是x2＋(y＋10.5)2＝14.52(0≤y≤4).把点D的横坐标x＝－5代入上式，得y≈3.1.由于船在水面以上高3 m,3＜3.1，所以该船可以从桥下通过.
例4一个小岛的周围有环岛暗礁，暗礁分布在以小岛中心为圆心，半径为20km的圆形区域内，已知小岛中心位于轮船正西40km处，港口位于小岛中心正北30km处.如果轮船沿直线返港，那么它是否会有触礁危险？
分析：先画出示意图,了解小岛中心、轮船、港口的方位和距离,如图,根据题意，建立适当的平面直角坐标系，求出暗礁所在区域的边缘圆的方程，以及轮船返港直线的方程，利用方程判断直线与圆的位置关系，进而确定轮船是否有触礁危险.
解：以小岛的中心为原点O,东西方向为x轴，建立如图所示的直角坐标系，为了运算的简便，我们取10km为单位长度，则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
由△=(-72)2-4×25×80<0,可知方程组无解.
所以直线l与圆O相离，轮船沿直线返港不会有触礁危险.
思考:你还能用其他方法解决上述问题吗？
用坐标法解决几何问题时，先用坐标和方程表示相应的几何元素：点、直线、圆，将几何问题转化为代数问题；然后通过代数运算解决代数问题；最后解释代数运算结果的几何含义，得到几何问题的结论，这就是用坐标法解决平面几何问题的“三步曲”： 第一步：建立适当的平面直角坐标系，用坐标和方程表示问题中的几何要素，如点、直线、圆，把平面几何问题转化为代数问题； 第二步：通过代数运算，解决代数问题； 第三步：把代数运算的结果“翻译”成几何结论.
比较坐标法与向量法，它们在解决几何问题时，有什么异同点？
向量法是将点、线、面等几何要素用向量表示，对这些向量进行运算，然后把向量运算的结果“翻译”成关于点、线、面的相应结果，由于向量线性运算给向量表示几何要素带来的便利性（由数乘向量和向量加法这两种运算可以把平面内任意向量表示成两个不共线向量的线性组合）,以及向量数量积运算在刻画长度与角度方面的强大功能，使得向量法在解决几何问题中发挥了巨大的作用，使许多问题的解决变得方便且简捷.
例4.如图所示，在圆O上任取C点为圆心，作圆C与圆O的直径AB相切于D，圆C与圆O交于点E，F，且EF与CD相交于H，求证：EF平分CD.
证明　以AB所在直线为x轴，O为坐标原点，建立平面直角坐标系，如图所示，设|AB|＝2r，D(a,0)，
∴圆O：x2＋y2＝r2，
如图，直角△ABC的斜边长为定值2m，以斜边的中点O为圆心作半径为n的圆，直线BC交圆于P，Q两点，求证：|AP|2＋|AQ|2＋|PQ|2为定值.
证明　如图，以O为坐标原点，以直线BC为x轴，建立平面直角坐标系，于是有B(－m,0)，C(m,0)，P(－n,0)，Q(n,0).设A(x，y)，由已知，点A在圆x2＋y2＝m2上.|AP|2＋|AQ|2＋|PQ|2＝(x＋n)2＋y2＋(x－n)2＋y2＋4n2＝2x2＋2y2＋6n2＝2m2＋6n2(定值).
设半径为3 km的圆形村落，A、B两人同时从村落中心出发，A向东，B向北，A出村后不久改变前进方向，斜着沿切于村落圆周的方向前进，后来恰好与B相遇，设A、B两人的速度一定，其比为3∶1，问A、B两人在何处相遇？
解　由题意以村中心为原点，正东方向为x轴的正方向，正北方向为y轴的正方向，建立直角坐标系，如图，设A、B两人的速度分别为3v km/h，v km/h，设A出发a h，在P处改变方向，又经过b h到达相遇点Q，则P(3av,0)，Q(0，(a＋b)v)，则|PQ|＝3bv，|OP|＝3av，|OQ|＝(a＋b)v.在Rt△OPQ中，|PQ|2＝|OP|2＋|OQ|2得5a＝4b.
由PQ与圆x2＋y2＝9相切，
1.一辆卡车宽1.6 m，要经过一个半圆形隧道(半径为3.6 m)，则这辆卡车的平顶车篷篷顶距地面高度不得超过(　　)A.1.4 m B.3.5 m C.3.6 m D.2.0 m
2.据气象台预报：在A城正东方300 km的海面B处有一台风中心，正以每小时40 km的速度向西北方向移动，在距台风中心250 km以内的地区将受其影响.从现在起经过约________h，台风将影响A城，持续时间约为________h(结果精确到0.1 h).
一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？