湘教版（2019）必修 第二册1.6 解三角形随堂练习题

这是一份湘教版（2019）必修 第二册1.6 解三角形随堂练习题，共7页。试卷主要包含了故选A等内容，欢迎下载使用。

题组一 测量距离问题
1.如图,设A、B两点在河的两岸,测量者与A在河的同侧,在河岸边选定一点C,测得AC的长为50 m,∠ACB=45°,∠CAB=105°,则A、B两点间的距离为( )
A.502 mB.503 mC.252 mD.2522 m
2.(2020河南平顶山高二上期末)一艘轮船以18海里/时的速度沿北偏东40°的方向直线航行,在行驶到某处时,测得该轮船南偏东20°方向10海里处有一灯塔,继续行驶20分钟后,轮船与灯塔的距离为( )
A.17海里B.16海里C.15海里D.14海里
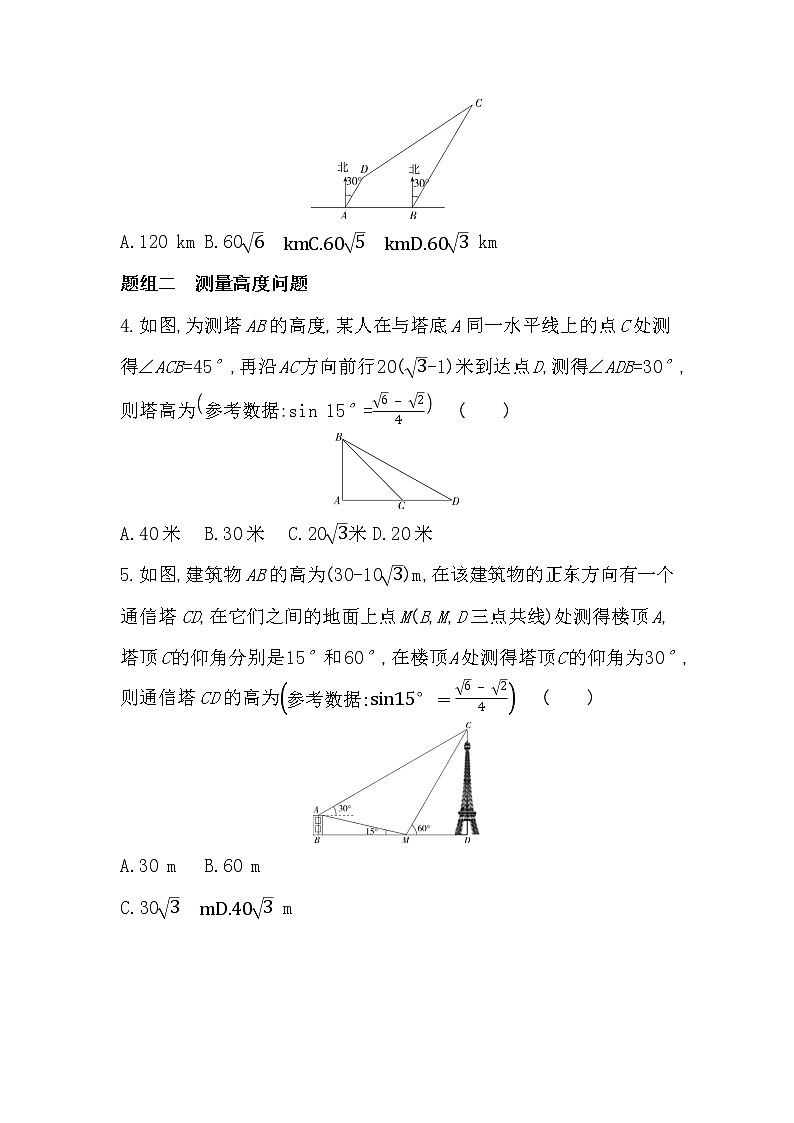
3.(2020河南信阳高三第一次教学质量检测)如图,有四座城市A、B、C、D,其中B在A的正东方向,且与A相距120 km,D在A的北偏东30°方向,且与A相距60 km,C在B的北偏东30°方向,且与B相距6013 km.一架飞机从城市D出发,以360 km/h的速度向城市C飞行,飞行了15 min,接到命令改变航向,飞向城市B,此时飞机距离城市B( )
A.120 kmB.606 kmC.605 kmD.603 km
题组二 测量高度问题
4.如图,为测塔AB的高度,某人在与塔底A同一水平线上的点C处测得∠ACB=45°,再沿AC方向前行20(3-1)米到达点D,测得∠ADB=30°,则塔高为参考数据:sin 15°=6-24( )
A.40米B.30米C.203米D.20米
5.如图,建筑物AB的高为(30-103)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为参考数据:sin15°=6-24( )
A.30 mB.60 m
C.303 mD.403 m
6.如图所示,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的山坡向山顶走1 000 m到达S点,又测得山顶仰角∠DSB=75°,则山高BC为( )
A.5002 mB.200 m
C.1 0002 mD.1 000 m
题组三 测量角度问题
7.如图,在某海岸A处发现北偏东30°方向、距离A处1海里的B处有一艘走私船,在A处北偏西60°方向、距离A处3海里的C处的缉私船奉命以53海里/时的速度追截走私船,此时,走私船以5海里/时的速度从B处按照北偏东30°方向逃窜,则缉私船能最快追上走私船的航行方向是( )
A.北偏东30°B.北偏东45°
C.北偏东60°D.正东
8.学校里有一棵树,甲同学在A地测得树尖的仰角为45°,乙同学在B地测得树尖的仰角为30°,量得AB=AC=10 m,树根部为C(A、B、C在同一水平面上),则∠ACB= .
答案全解全析
基础过关练
1.A 在△ABC中,∠ACB=45°,∠CAB=105°,则∠ABC=30°,
由正弦定理,得ABsin∠ACB=ACsin∠ABC,
则AB=AC·sin∠ACBsin∠ABC=50×2212=502(m).故选A.
2.D 如图所示,记轮船行驶到某处的位置为A,灯塔的位置为B,20分钟后轮船的位置为C,则AB=10,AC=6,∠CAB=120°,所以BC2=102+62-2×10×6×-12=196,所以BC=14,即20分钟后,轮船与灯塔的距离为14海里.
3.D 取AB的中点E,连接DE,BD.设飞机飞行了15 min到达F点,连接BF,如图所示,则BF即为所求.
因为E为AB的中点,且AB=120 km,
所以AE=60 km,
又∠DAE=90°-30°=60°,AD=60 km,
所以三角形DAE为等边三角形,
所以DE=60 km,∠ADE=60°,
在等腰三角形EDB中,∠DEB=120°,
所以∠EDB=∠EBD=30°,
所以∠ADB=90°,由勾股定理得BD2=AB2-AD2=1202-602=10 800,
所以BD=603 km,
因为∠CBE=90°+30°=120°,∠EBD=30°,所以∠CBD=90°,
所以CD=BD2+BC2=10 800+(6013)2=240 km,
所以cs∠BDC=BDCD=603240=34,
因为DF=360×14=90 km,
所以在三角形BDF中,
BF2=BD2+DF2-2×BD×DF×cs∠BDF
=(603)2+902-2×603×90×34=10 800,
所以BF=603 km,即此时飞机距离城市B 603 km.
4.D 在△BCD中,由正弦定理可得,CDsin∠CBD=BDsin∠BCD,又知CD=20(3-1)米,sin∠BCD=sin(180°-45°)=22,
sin∠CBD=sin(45°-30°)=sin 15°=6-24,
∴BD=CD·sin∠BCDsin∠CBD=20(3-1)×226-24=40(米),
由△ABD为直角三角形,∠ADB=30°,可得AB=20米,即塔高为20米.
5.B 如图所示,过点A作AE⊥CD,垂足为E.
在△ABM中,
AM=ABsin15°=206(m),
又知在△AMC中,∠AMC=105°,∠ACM=30°,
∴ACsin105°=206sin30°,
∵sin 15°=6-24,
∴sin 105°=sin(90°+15°)=cs 15°=6+24,
∴AC=(60+203)m,
∴CE=12AC=(30+103)m,
∴CD=CE+ED=CE+AB=(30+103)+(30-103)=60(m).
6.D 由题图可知,∠BSA=360°-75°-150°=135°,又∠SAB=45°-30°=15°,
∴∠ABS=30°,
在△ABS中,ASsin30°=ABsin135°,
∴AB=AS·sin135°sin30°=1 000×2212
=1 0002(m),
∴BC=AB·sin∠BAC=1 0002·sin 45°=1 000(m).
7.C 如图,
设缉私船在D处追上走私船,所用时间为t小时,则CD=53t海里,BD=5t海里.
由题意可知∠CAD=90°,AC=3海里,AB=1 海里,
∴AD=(5t+1)海里,
由勾股定理可得(5t+1)2+3=75t2,
解得t=25或t=-15(舍去).
∴AD=3海里,故tan∠DCA=ADAC=3,
∴∠DCA=60°,∴∠NCD=60°(N在C的正北方向),故选C.
8.答案 30°
解析 如图,设树尖为点D,由题意知,AC=10 m,∠DAC=45°,∴DC=10 m.
又∵∠DBC=30°,∴BC=103 m.
由余弦定理得,cs∠ACB=
102+(103)2-1022×10×103=32,∴∠ACB=30°.