2021年北京朝阳区劲松三中八年级上期末数学试卷

这是一份2021年北京朝阳区劲松三中八年级上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 原子是化学反应中不可再分的基本微粒，由原子核和电子组成．某原子的直径约为 0.000000000196 m，可用科学记数法表示为
A. 1.96×1010 mB. 19.6×1011 mC. 19.6×10−11 mD. 1.96×10−10 m

2. 2017 年 6 月北京国际设计周面向社会公开征集“二十四节气”标识系统设计，以期通过现代设计的手段，尝试推动我国非物质文化遗产创新传承与发展．下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是
A. B.
C. D.

3. 若分式 5a−b3a+2b 有意义，则 a，b 满足的关系是
A. 3a≠2bB. a≠15bC. b≠−23aD. a≠−23b

4. 下列式子不正确的是
A. a2⋅a3=a5B. ab2=a2b2C. a0=1a≠0D. a32=a5

5. 正 n 边形的每个内角都是 120∘，则 n 的值是
A. 3B. 4C. 6D. 8

6. 下列四个数轴的画法中，规范的是
A. B.
C. D.

7. 若等腰直角三角形的外接圆半径的长为 2，则其内切圆半径的长为
A. 2B. 22−2C. 2−2D. 2−1

8. 如果 m 是任意实数，那么点 Pm−4,m+1 一定不在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

二、填空题（共8小题；共40分）
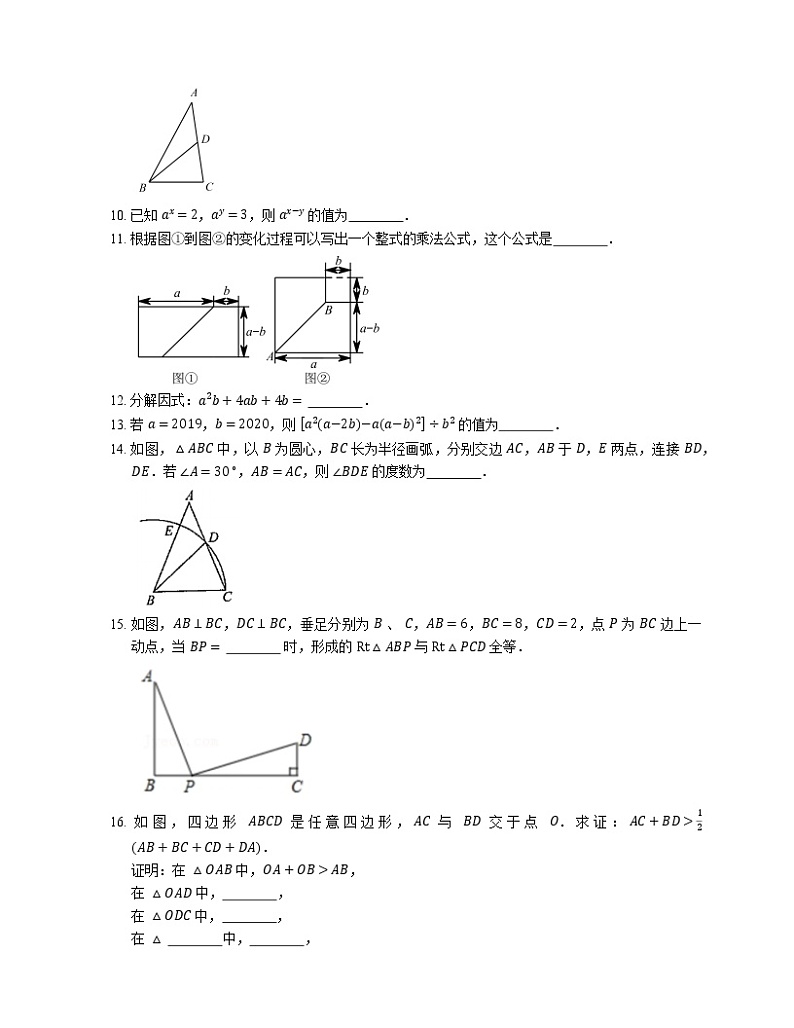
9. 如图，已知 BD 是 △ABC 的中线，AB=5，BC=3，△ABD 和 △BCD 的周长差是 ．

10. 已知 ax=2，ay=3，则 ax−y 的值为 ．

11. 根据图①到图②的变化过程可以写出一个整式的乘法公式，这个公式是 ．

12. 分解因式：a2b+4ab+4b= ．

13. 若 a=2019，b=2020，则 a2a−2b−aa−b2÷b2 的值为 ．

14. 如图，△ABC 中，以 B 为圆心，BC 长为半径画弧，分别交边 AC，AB 于 D，E 两点，连接 BD，DE．若 ∠A=30∘，AB=AC，则 ∠BDE 的度数为 ．

15. 如图，AB⊥BC，DC⊥BC，垂足分别为 B 、 C，AB=6，BC=8，CD=2，点 P 为 BC 边上一动点，当 BP= 时，形成的 Rt△ABP 与 Rt△PCD 全等．

16. 如图，四边形 ABCD 是任意四边形，AC 与 BD 交于点 O．求证：AC+BD>12AB+BC+CD+DA．
证明：在 △OAB 中，OA+OB>AB，
在 △OAD 中， ，
在 △ODC 中， ，
在 △ 中， ，
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+BC+CD+DA，
即 ，
即 AC+BD>12AB+BC+CD+DA．

三、解答题（共11小题；共143分）
17. 化简：4xx2−4−2x−2−1．
圆圆的解答如下：4xx2−4−2x−2−1=4x−2x+2−x2−4=−x2+2x
圆圆的解答正确吗?如果不正确，写出正确的答案．

18. 化简：x−22−4xx−1+2x−12x+1．

19. 解方程：x−2−x2=1−x−33．

20. 已知：如图，点 A，C，D，B 在同一条直线上，AC=BD，AF=BE，∠A=∠B．求证：∠E=∠F．

21. 如图．
（1）在网格中画出 △ABC 关于 y 轴对称的 △A1B1C1．
（2）在 y 轴上确定一点 P，使 △PAB 周长最短．（只需作图，保留作图痕迹）
（3）写出 △ABC 关于 x 轴对称的 △A2B2C2 的各顶点坐标．

22. 如图，在 Rt△ABC 中，∠ABC=90∘，点 D 在边 AB 上，使 DB=BC，过点 D 作 EF⊥AC，分别交 AC 于点 E 、 CB 的延长线于点 F．求证：AB=BF．

23. 依法纳税是每个公民应尽的义务．新税法规定：居民个人的综合所得，以每一纳税月收入减去费用 5000 元以及专项扣除、专项附加扣除和依法确定的其他扣除后的余额，为个人应纳税所得额．已知李先生某月的个人应纳税所得额比张先生的多 1500 元，个人所得税税率相同情况下，李先生的个人所得税税额为 76.5 元，而张先生的个人所得税税额为 31.5 元．求李先生和张先生应纳税所得额分别为多少元?个人所得税税率=个人所得税税额应纳税所得额

24. 如图，已知：四边形 ABCD 中，AB=CD，E，F，G 分别是 AD，BC，BD 的中点，GH 平分 ∠EGF，交 EF 于点 H．求证：GH⊥EF．

25. 如图所示，∠B=∠C=90∘，点 M 是 BC 的中点，DM 平分 ∠ADC．求证：AM 平分 ∠DAB．

26. 点 P 到 ∠AOB 的距离定义如下：点 Q 为 ∠AOB 的两边上的动点，当 PQ 最小时，我们称此时 PQ 的长度为点 P 到 ∠AOB 的距离，记为 dP,∠AOB．特别的，当点 P 在 ∠AOB 的边上时，dP,∠AOB=0．在平面直角坐标系 xOy 中，四边形 OABC 是以点 O0,0，A4,0，B4,4，C0,4 为顶点的正方形，作射线 OB，则 ∠AOB=45∘．
（1）如图 1，点 P1−1,0，P20,2，P31,−2 的位置如图所示，请用度量的方式，判断点 P1，P2，P3 中到 ∠AOB 的距离等于 1 的点是 ；
（2）已知点 P 在 ∠AOB 的内部，且 dP,∠AOB=1，
①若点 P 的横纵坐标都是整数，请写出一个满足条件的图点 P 的坐标 ；
②请在图 1 中画出所有满足条件的点 P；
（3）如图 2，已知点 E0,−8，F−2,2，G7,2，记射线 EF 与射线 EG 组成的图形为图形 V．若点 P 在图形 V 上，满足 dP,∠AOB=22 的点 P 有 个．

27. （1）（1）问题发现
如图1，△ACB 和 △DCE 均为等边三角形，点 A 、 D 、 E 在同一直线上，连接 BE .
填空：
（1）∠AEB 的度数为 ；
（2）线段 BE 和 AD 之间的数量关系是 ．
（2）拓展探究
如图2，△ACB 和 △DCE 均为等腰直角三角形，∠ACB=∠DCE=90∘ ， 点 A 、 D 、 E 在同一直线上，CM 为 △DCE 中 DE 边上的高，连接 BE．请判断 ∠AEB 的度数及线段 CM 、 AE 、 BE 之间的数量关系，并说明理由．
（3）解决问题
如图3，在正方形 ABCD 中，CD=2．若点 P 满足 PD=1 ，且 ∠BPD=90∘，请直接写出点 A 到 BP 的距离．
答案
第一部分
1. D【解析】绝对值小于 1 的正数也可以用科学记数法表示，一般形式为 a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，n 由原数左边起第一个不为零的数字前面的 0 的个数所决定．所以 0.000000000196=1.96×10−10．
2. D
3. D
4. D
5. C
6. C【解析】数轴是规定了原点、正方向、单位长度的直线，选项A的数轴单位长度不一致，因此选项A不正确；选项B的数轴无原点，因此选项B不正确；选项C符合数轴的画法，正确；选项D的数轴没有正方向，因此选项D不正确．
7. B
8. D
第二部分
9. 2
10. 23
11. a+ba−b=a2−b2
12. ba+22
13. −2019
【解析】原式=a3−2a2b−aa2−2ab+b2÷b2=a3−2a2b−a3−2a2b+ab2÷b2=a3−2a2b−a3+2a2b−ab2÷b2=−ab2÷b2=−a,
∵a=2019，
∴原式=−2019．
14. 67.5∘
15. 2
【解析】当 BP=2 时，Rt△ABP≌Rt△PCD，
∵BC=8，BP=2，
∴PC=6，
∵AB⊥BC，DC⊥BC，
∴∠B=∠C=90∘，
在 △ABP 和 △PCD 中 AB=PC=6,∠B=∠C=90∘,BP=CD=2,
∴△ABP≌△PCDSAS，
故答案为：2．
16. OA+OD>DA，OD+OC>CD，OBC，OB+OC>BC，2AC+BD>AB+BC+CD+DA
第三部分
17. 圆圆的解答错误，正确解法：
4xx2−4−2x−2−1=4xx−2x+2−2x+2x−2x+2−x−2x+2x−2x+2=4x−2x−4−x2+4x−2x+2=2x−x2x−2x+2=−xx+2.
18. 原式=x2−4x+4−4x2+4x+4x2−1=x2+3.
19. x=1811．
20. ∵AC=BD，
∴AC+CD=BD+CD，
即 AD=BC．
在 △ADF 和 △BCE 中，AD=BC,∠A=∠B,AF=BE,
∴△ADF≌△BCESAS，
∴∠E=∠F．
21. （1） 如图所示：△A1B1C1，即为所求．
（2） 连接 AB1 或 BA1 交 y 轴于点 P，则点 P 即为所求．
（3） A2−3,−2，B2−4,3，C2−1,1．
22. ∵EF⊥AC，
∴∠F+∠C=90∘．
∵∠ABC=90∘，
∴∠A+∠C=90∘，
∴∠A=∠F．
∵DB=BC，∠FBD=∠ABC，
∴△FBD≌△ABC．
∴AB=BF．
23. 设张先生应纳税所得额为 x 元，则李先生应纳税所得额为 x+1500 元．
依题意得，
76.5x+1500=31.5x.
解得
x=1050.
经检验：x=1050 是原方程的根且符合题意，
当 x=1050 时，x+1500=2550，
答：李先生和张先生的应纳税所得额分别为 2550 元，1050 元．
24. 提示：先用三角形中位线定理证得 △EGF 是等腰三角形，再利用等腰三角形三线合一证得垂直．
25. 如图所示，
过点 M 作 MN⊥AD，垂足为点 N．
∵DM 平分 ∠ADC，MN⊥AD，MC⊥DC，
∴MN=MC．
又 ∵ 点 M 是 BC 的中点，
∴MB=MC．
∴MN=MB．
∵MN⊥AD，MB⊥AB，
∴ 点 M 在 ∠DAB 的平分线上，
即 AM 平分 ∠DAB．
26. （1） P1，P2
【解析】如图 1 中，
通过测量法，可知点 P2 到直线 OB 的距离为 1，
OP1=1，OP3>1，
∴ 点 P1，P2，P3 中到 ∠AOB 的距离等于 1 的点是 P1，P2．
（2） ①答案不唯一，如 3,1，4,1，5,1 等；
②如图 1 中，所有满足条件的点 P 在 ∠MJN 的边上．
（3） 6
【解析】如图 2 中，满足条件的点 P 在图中的红线上，红线与 ∠FEG 有 6 个交点（其中一个交点是 EG 与 FC 的交点，图中没有画出来），
故满足条件的点 P 有 6 个．
27. （1） ① 60∘ ；② AD=BE
（2） ∵△ACB 和 △DCE 均为等腰直角三角形，∠ACB=∠DCE=90∘，
∴AC=BC，CD=CE，∠ACB=∠DCB=∠DCE−∠DCB，即 ∠ACD=∠BCE .
∴△ACD≌△BCE .
∴AD=BE，∠BEC=∠ADC=135∘．
∴∠AEB=∠BEC−∠CED=135∘−45∘=90∘．
在等腰直角三角形 DCE 中，CM 为斜边 DE 上的高，
∴CM=DM=ME .
∵DE=2CM ，
∴AE=DE+AD=2CM+BE .
（3） PD=1，∠BPD=90∘，
∴BP 是以点 D 为圆心、以 1 为半径的 OD 的切线，点 P 为切点．
第一种情况：如图①，过点 A 作 AP 的垂线，交 BP 于点 Pʹ，
可证 △APD≌△APʹB，PD=PʹB=1，CD=2 .
∴BD=2，BP=3 .
∴AM=12PPʹ=12PB−BPʹ=3−12 .
第二种情况如图②，
可得 AM=12PPʹ=12PB+BPʹ=3+12