数学八年级上册4 一次函数的应用课文内容课件ppt

这是一份数学八年级上册4 一次函数的应用课文内容课件ppt，共25页。PPT课件主要包含了生活中的图象，干旱造成的灾情，回答下列问题，跟踪练习，ycm，拔尖自助餐，当堂检测，本节课你学到了什么，感悟与反思等内容，欢迎下载使用。

1.知识目标： （1）提高学生的读图能力，解决与两个一次函数 相关的图象信息题. （2）进一步培养学生数形结合思想，以及分析、解 决问题的能力，提高思维能力. （3）通过小组合作学习，培养学生探究意识.
2.教学重点 读懂图象，并从图象中获取已知条件解决问题.3.教学难点 同一坐标的两个函数的联系.
O 10 20 30 40 50 t/天
1 2001 000800600400200
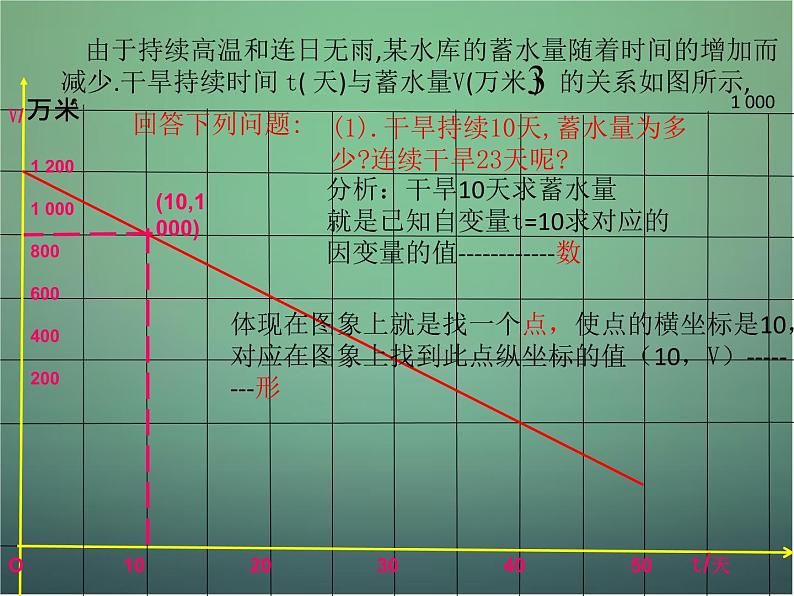
由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.干旱持续时间 t( 天)与蓄水量V(万米 ) 的关系如图所示,
(1).干旱持续10天,蓄水量为多少?连续干旱23天呢?
分析：干旱10天求蓄水量就是已知自变量t=10求对应的因变量的值------------数
体现在图象上就是找一个点，使点的横坐标是10，对应在图象上找到此点纵坐标的值（10，V）--------形
0 10 20 30 40 50 t/天
12001000800600400200
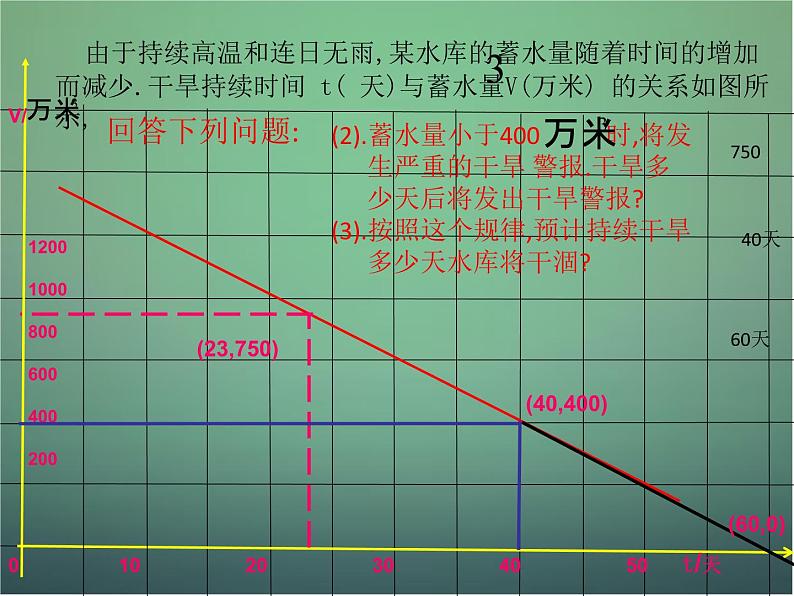
由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.干旱持续时间 t( 天)与蓄水量V(万米) 的关系如图所示,
(2).蓄水量小于400 时,将发 生严重的干旱 警报.干旱多 少天后将发出干旱警报?(3).按照这个规律,预计持续干旱 多少天水库将干涸?
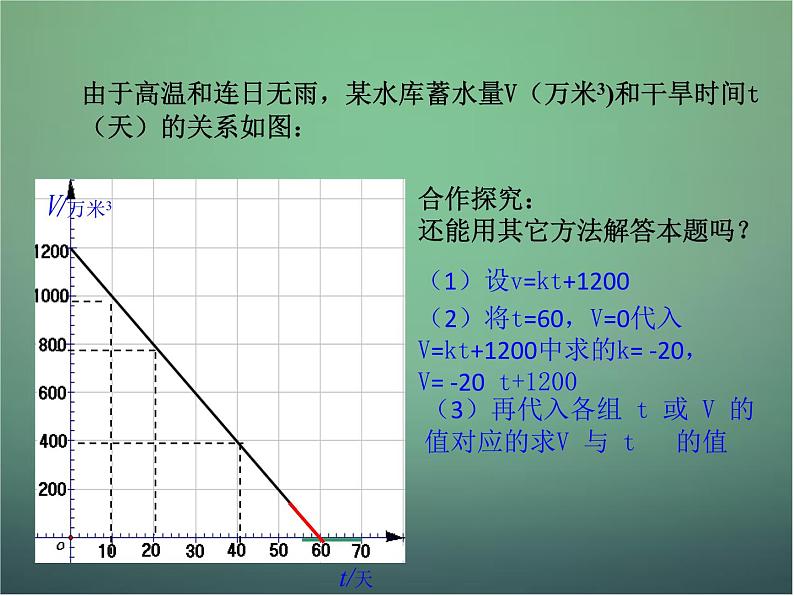
由于高温和连日无雨，某水库蓄水量V（万米3)和干旱时间t（天）的关系如图：
合作探究：还能用其它方法解答本题吗？
（1）设v=kt+1200
（2）将t=60，V=0代入V=kt+1200中求的k= -20，V= -20 t+1200
（3）再代入各组 t 或 V 的值对应的求V 与 t 的值
议一议 一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系？
从“数”的方面看,当一次函数 y =0.5x+1 的函数值为0时,相应的自变量的值即为方程 0.5x+1=0 的解； 从“行”的方面看,函数 y =0.5x+1 与 x 轴交点的横坐标即为方程 0.5x+1=0 的解.
例1 根据图象回答问题： （1）一箱汽油可供摩托车行驶多少千米？
解：观察图象，得(1)当y＝0时，x＝500,因此一箱汽油可供摩托车行驶500千米.
（3）摩托车的剩余油量小于1升时，摩托车将自动报警.行驶多少千米后，摩托车将自动报警？
（2）摩托车每行驶100千米消耗多少升汽油？
（2）x从0增加到100时，y从10减少到8，减少了2， 因此摩托车每行驶100千米2消耗升汽油.
（3）当y＝1时，x＝450，因此行驶了450千米后，摩托车将自动报警.
例2 在弹性限度内,弹簧的长度 y（厘米）是所挂物体质量x（千克）的一次函数.一根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米.请写出 y 与x之间的关系式，并求当所挂物体的质量为4千克时弹簧的长度.
解：设y=kx+b,根据题意，得
14.5=b ①16=3k+b ②将b=14.5代入②，得k=0.5
所以在弹性限度内，y=0.5x+14.5
当x=4时，y=0.5×4+14.5=16.5 即物体的质量为4千克时，弹簧长度为16.5厘米.
1.某植物t天后的高度为ycm，图中的l 反映了y与t之间的关系，根据图象回答下列问题：
（1）植物刚栽的时候多高？
（2）3天后该植物多高？
（3）几天后该植物高度可达21 cm
(1)旅客最多可免费携带多少千克行李？
⑵超过30千克后，每千克需付多少元？
3. 小明在电信局办理了某种电话话费套餐，该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费，办理后某月手机话费y元和通话时间x的关系图如下：
观察图象形状,有何特点，你知道该电话套餐的内容吗？
⑴该话费套餐的月租费是多少元?
⑵每分钟通话需多少元?
100分钟后每分钟通话：
100分钟前每分钟通话：
4.某植物t天后的高度为y厘米,图中反映了y与t之间的关系，根据图象回答下列问题：
(1)植物刚栽的时候多高？
（2）3天后该植物高度为多少？
（3）几天后该植物高度可达21cm?
（4）先写出y与t的关系式，再计算长到100cm需几天？
某蔬菜基地要把一批新鲜蔬菜运往外地，有两种运输方式选择，主要参考数据如下：
（1）请分别写出汽车、火车运输的总费用y1（元）、y2(元）与运输路程x（km)之间的函数关系；
（2）你能说出用哪种运输队方式好吗？
解： （1）y1=200＋4.5x y2=410＋2.4x
y1=200＋4.5x
y2=410＋2.4x
y1=200＋4.5x（汽车）
y2=410＋2.4x（火车）
（2）当y1=y2时，x=100 .从函数图象看，当x=100时，两个函数的图象相交于一点，此时两个自变量相同，函数值相同.我认为：当运输路程为100km时，运输方式可选择汽车或火车；当运输路程小于100km时，运输方式可选择汽车；当运输路程大于100km时，运输方式可选择火车；
1. 假如出租车在市内的收费方式如下：３千米以内（含３千米）6元， 超过３千米的部分平均每千米收 1 元，设小亮乘坐出租车的路程为x（千米） ，需付车费为y（元）. 　（1）求y与x之间的函数关系式，并画出函数的大致图象.　（2）如果小亮乘出租车行驶 2 千米，要付车费多少元？　（３）如果小亮一次付车费 8 元，你知道他乘车的路程吗？
（2）由图象得当x＝2时，y ＝ 6（元）（3）由图象得y ＝8应代入y＝ x＋3 ，即：8＝ x＋3 ，所以x＝5（千米）．
2.　柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克(1)写出余油量Q与时间t的函数关系式；(2)画出这个函数的图象.
解：（１）设Q ＝kt＋b.把t=0，Q=40；t=3.5，Q=22.5分别代入上式，得
解析式为：Q＝－５t+40　　(0≤t≤8)．
（２）取t=0，得Q=40；取t=８，得Q=０.描出点A（０，40），B（8，0）.然后连成线段AB即是所求的图形.
点评：（1）求出函数关系式时，必须找出自变量的取值范围. （2）画函数图象时，应根据函数自变量的取值范围来确定图象的范围.
图象是包括两端点的线段
3.某商场文具部的某种笔售价25元，练习本每本售价5元.该商场为了促销制定了两种优惠方案供顾客选择.甲：买一支笔赠送一本练习本.乙：按购买金额打九折付款.某校欲购这种笔10支，练习本x（x ≥10)本，如何选择方案购买呢？
解：甲、乙两种方案的实际金额y元与练习本x本之间的关系式是：
y甲=(x-10)×5+25×10=5x+200 (x ≥10)
y乙=(10×25+5x) ×0.9=4.5x+225 (x ≥10)
由图象可以得出同样结果
当10 ≤ x<50时，y甲当x=50时，y甲=y乙
当x>50时，y甲>y乙
（1）学会解较为复杂的一次函数的应用题；
（2）学会把复杂的图象转化为几个简单的图象去解决问题.