人教版新课标A必修4第一章 三角函数1.6 三角函数模型的简单应用课后测评

高中数学必修４ 第一章《三角函数》测试题(4)

的图象、三角函数模型的简单应用

A组

一、选择题:共6小题

1.(易 图象变换)将函数的图象向左平移个单位,得到的图象,则等于(      )                                                                                                                                     

A.  B.  C.   D.

2.(易 图像变换)将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的解析式是(    )

A.                B.

C.            D.

3.(易 图象)函数在区间的简图是(   )

4.(中 诱导公式和图像变换)已知函数的最小正周期为,为了得到函数的图象,只要将的图象(    )

A.向左平移个单位长度          B.向右平移个单位长度         

C.向左平移个单位长度          D.向右平移个单位长度    

5.(中 简谐振动)已知简谐振动的振幅是,图像上相邻最高点和最低点的距离是5,且过点,则该简谐振动的频率和初相是(   )

A.            B.           C.             D.

6.(难 平移与性质)把函数的图象向左平移的单位,所得到的函数为偶函数,则的最小值是(    )

A.            B.            C.               D.                                    

二、填空题:共3小题

7.(易 图像)函数(为常数,)在闭区间上的图象如图所示,

则=       .

8.(中  图像)已知函数y=sin(x+)(>0,－<)的图像如图所示,则=________________  

9.(中 平移与性质)把函数y = cos(x+)的图象向左平

移m个单位(m>0),所得图象关于y轴对称,则m的最

小值是_________.

三、解答题:共2小题

10.(中 图像与性质)设函数图像的一条对称轴是直线.

(1)求;

(2)求函数的单调增区间;

(3)画出函数在区间上的图像.

11.函数的图象如图所示,其中A>0,ω>0,0<<,

(1)求它的解析式;

(2)说明该函数的图像可由y=sinx的图像经过怎样的变换而得到.

B组

一、选择题:共6小题

1.(易 图象变换与诱导公式)要得到函数的图象,只需将函数的图象(   )

A.向右平移个单位        B.向右平移个单位

C.向左平移个单位         D.向左平移个单位

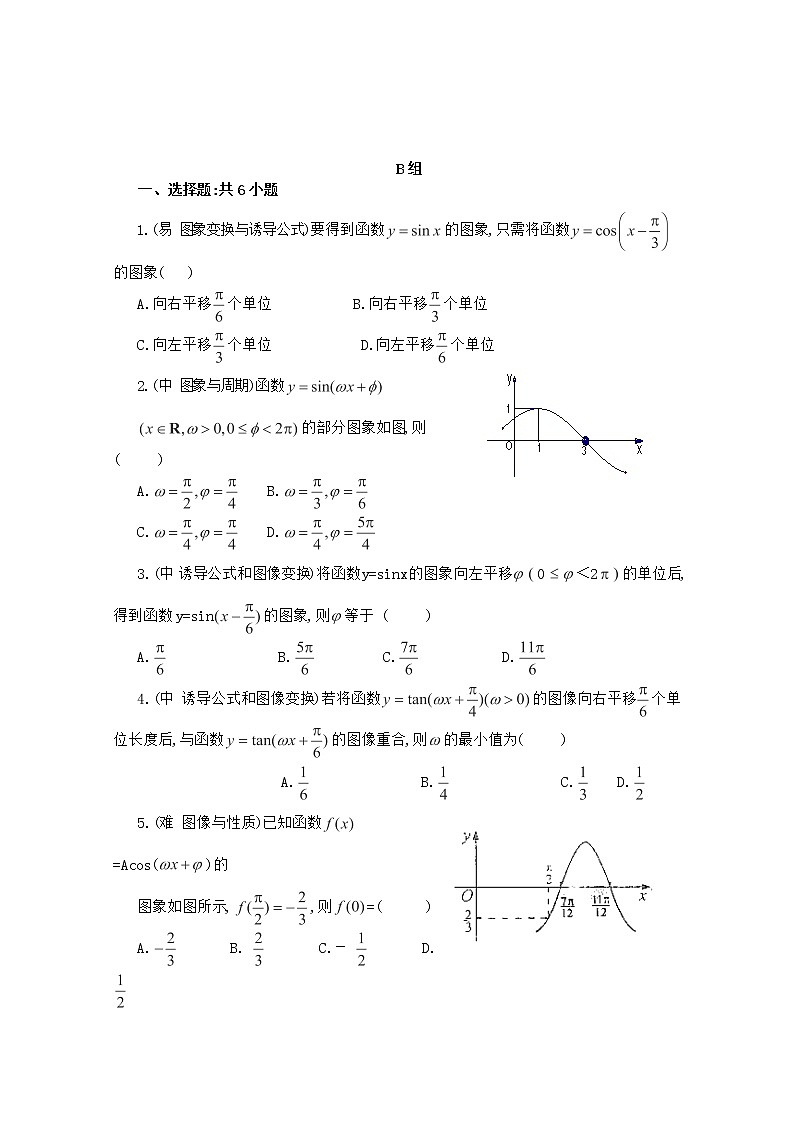
2.(中 图象与周期)函数

的部分图象如图,则(     )

A. B.

C. D.

3.(中 诱导公式和图像变换)将函数y=sinx的图象向左平移0 ＜2的单位后,得到函数y=sin的图象,则等于 (     )

A.               B.         C.           D.     

4.(中 诱导公式和图像变换)若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为(     )

 A.   B.     C.   D.

5.(难 图像与性质)已知函数=Acos()的

图象如图所示,,则=(      )

A.       B.        C.－        D.  

6.(难 图像与周期性)函数图像如图所示,则的值等于(     )

A.       B.      C.        D.1

二、填空题:共3小题

7.(中 图像)已知函数的图像如图

所示,则               .

8.(中 图像变换)已知函数的图象上的每一点的纵坐标扩大到原来的倍,横坐标扩大到原来的倍,然后把所得的图象沿轴向左平移,这样得到的曲线和的图象相同,则已知函数的解析式为_______________________________.

9.(中 图像与性质)如果函数的图像关于点中心对称,那么的最小值为___________

三、解答题:共2小题

10、(中 图像与性质)已知函数(其中)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.

(1)求的解析式;

(2)当,求的值域.    

11.(中 图像变换与性质)已知函数f(x)＝为偶函数,且函数y＝f(x)图象的两相邻对称轴间的距离为.

(1)求f()的值;

(2)将函数y＝f(x)的图象向右平移个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y＝g(x)的图象,求g(x)的单调递减区间.

C组

解答题:共2小题

1. (难 图像与性质)已知函数的图象中相邻两条对称轴间的距离为,且点是它的一个对称中心.

(1)求的表达式;

(2)若在上是单调递减函数,求的最大值.

2.(难 图像与变换)函数在同一个周期内,当时取最大值1,当时,取最小值.

(1)求函数的解析式

(2)函数的图象经过怎样的变换可得到的图象？

(3)若函数满足方程求在内的所有实数根之和.

参考答案

A组

1.C　函数的图象向左平移个单位,得到的图象,故

2.C 

3.A 由特殊值法可判定,取代入计算,知A正确.

4.A  由题知,

所以,故选择A

5.B 有题意可知,A=,,则T=8,,,

由,因为所以因此频率是,初相为

6.D 平移后的函数解析式为,因为它是偶函数,所以,即,所以的最小值是

7. 3 考查三角函数的周期知识,所以.

8. 由图可知,,∴,把代入有,

∴.

9.π  把函数y = cos(x+)的图象向左平移m个单位(m>0),得到图象y = cos(x++m),而此图象关于y轴对称故m的最小值是π　　

10.解:(1)∵是函数的图像的对称轴,∴

∴;

(2)由(1)知∴

由题意得

所以函数的单调增区间为;

(3)由得

故函数在区间上的图

象如图所示

11.解:(1)由图可知,A＝2,T＝,所以有ω＝,又函数过点,

故有,又此点位于单调增区间内,故有,

∴,又,所以,故它的解析式为.

(2)把y=sinx的图像上所有的点向左平移个单位,得到的图像,再把所得到的图像上的点的横坐标伸长为原来的2倍(纵坐标不变),得到的图像,

最后把所得到的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),

即可得到的图像.

B组

1.A ,由左加右减的原则,故选A.

2.C由,特殊点函数值,可得.

3.D由函数向左平移的单位得到的图象,由条件知函数可化为函数,易知比较各答案,

只有,所以选D.

4.D 向右平移个单位得

∴,得,又,∴.

5.B由图象可得最小正周期为,于是f(0)＝f(),注意到与关于对称,

所以f()＝－f()＝

6.C由图像可知,A=2,T=8,则,由,得,所以函数的解析式是,易求得,

故.

7.0由图象知最小正周期T＝()＝＝,故＝3,

又x＝时, f(x)＝0,即2)＝0,可得,

所以.

8. 

9. ∵函数的图像关于点中心对称

∴,得,由此得.故选A

10.解(1)由最低点为得A=2.

由x轴上相邻的两个交点之间的距离为得=,即,

由点在图像上得,即,

∴,得,

又,∴,于是;

(2)∵,∴,

当,即时,取得最大值2;当,即时,取得最小值－1,故的值域为[－1,2]   

11.解(1)因为f(x)为偶函数,所以,故

又因为0＜＜π,故＝.所以f(x)＝2sin(+)=2cos.

由题意得,所以,故f(x)=2cos2x.

∴;

(2)将f(x)的图象向右平移个个单位后,得到的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到的图象.

所以.

当(k∈),即4kπ＋≤x≤4kπ+ (k∈)时,g(x)单调递减.

因此g(x)的单调递减区间为　　　(k∈Z)

C组

1.解(1)由题意得的最小正周期为,∴,得.

∴,又是它的一个对称中心,

∴,得,

∴.

(2)由(1)得, ∵,

所以欲满足条件,必须,∴.即a的最大值为

2.解:(1)∵,∴,

又因∴又得

∴函数;

(2)的图象向右平移个单位得的图象,再由图象上所有点的横坐标变为原来的.纵坐标不变,得到的图象,

(3)∵的周期为,

∴在内恰有3个周期,

∴在内有6个实根且

同理,

故所有实数之和为.