初中数学第十一章 三角形11.2 与三角形有关的角本节综合教案

这是一份初中数学第十一章 三角形11.2 与三角形有关的角本节综合教案，共3页。教案主要包含了探索新知等内容，欢迎下载使用。


教
学
目
标
知识与技能
通过操作活动，探究并掌握三角形内角和性质，并能应用三角形内角和性质解决一些简单的实际问题。
过程与方法
经历观察、操作、想象、推理、交流，发展空间观念、推理能力和有条理的表达能力。
情感态度价值观
学会多角度寻求解决问题的途径,在操作中进行自觉思考,积累数学探索的经验
学习重点
三角形内角和定理
学习难点
三角形内角和定理的推理过程
学 习 过 程
教 师 活 动
学生活动
情境导入
两个面积不一样的三角形对话。（见课件）
二、探索新知
大胆猜测：
命题：三角形的三个内角的和等于180°
请学生思考该命题的题设和结论。
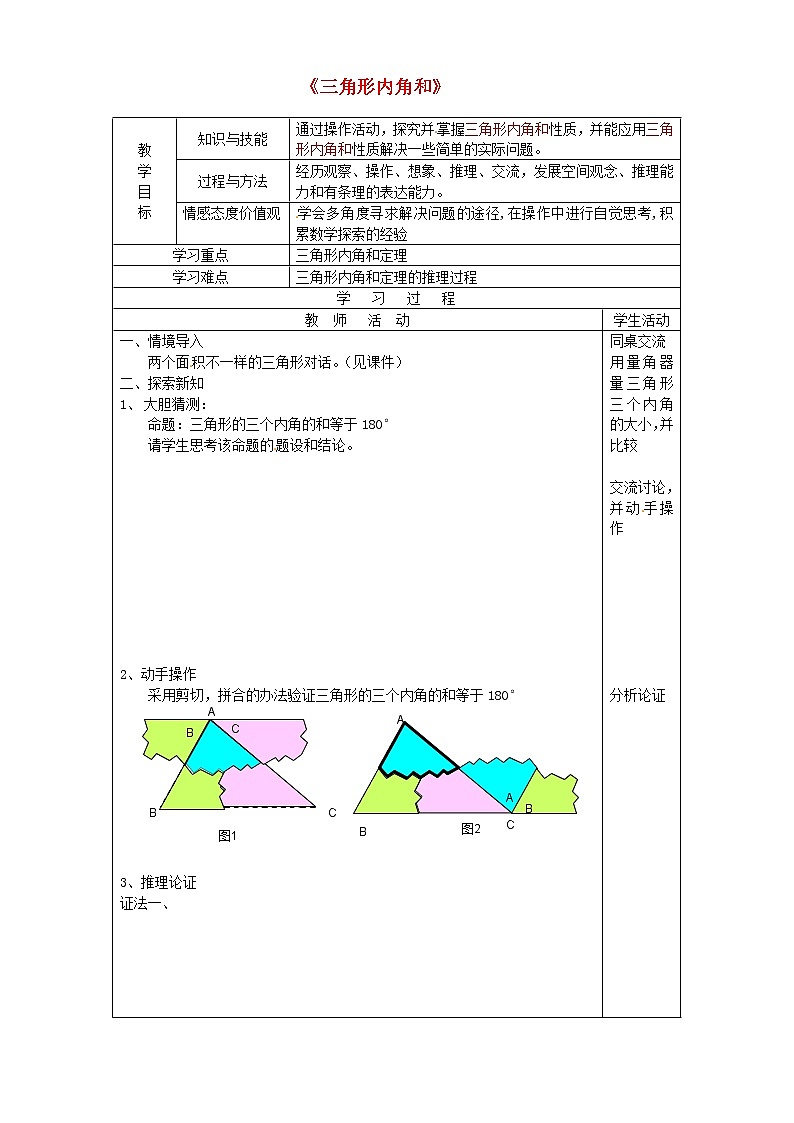
2、动手操作
采图1
图2
A
B
C
C
B
A
B
C
A
B
用剪切，拼合的办法验证三角形的三个内角的和等于180°
3、推理论证
证法一、

已知：△ABC
求证：∠A+∠B+∠C=180°
证明：略
证法二、

证法三：

4、归纳小结
命题：三角形的三个内角的和是180°
定理：三角形的三个内角的和是180°
推理
论
证
解答疑难几何图形问题时，在原图基础之上另外所作的具有极大价值的直线或者线段叫辅助线。作图时，画虚线，并且一条辅助线只能满足一个条件。
我们在证明三角形内角和定理的过程中，将三角形内角和问题转化熟悉的平角或两平行直线的同旁内角问题，用我们熟悉的知识、方法解决，这就是数学中常用的转化思想。
5、课堂练习一
（1）、在△ABC中,∠A=35°,∠ B=43°，则∠ C= 。
（2）、在△ABC中,∠C=90°,∠B=50°,则∠A = ＿＿＿＿。
（3）、在△ABC中, ∠A=40°,∠A=2∠B，则∠C = ＿＿＿＿。
6、例题分析
已知：三角形三个内角的度数之比为1:3:5，求这三个内角的度数。
解：（略）
7、课堂练习二
（1）、在△ABC中,∠A=75°,∠ B-∠ C=15°，则∠ C= 。
（2）三角形的三个内角度数之比为2：3：5，则这个三角形的三个内角的度数分别是：
课堂小结
定理：三角形的三个内角的和是180°
应用：
1、在三角形中，已知两个角的度数，可求另一个角的度数。
2、在三角形中，已知各角之间的数量关系，可求各角。
交流讨论
一个三角形中，最多有 个直角；
一个三角形中，最多有 个钝角；
一个三角形中，最大的角不能小于 度。
一个三角形中，最少有 个锐角；
课后反思
同桌交流
用量角器量三角形三个内角的大小，并比较
交流讨论，并动手操作
分析论证
归纳小结
练习
思考，讨论
练习
交流讨论
思考讨论