高中数学湘教版（2019）必修 第一册6.4 用样本估计总体图片ppt课件

这是一份高中数学湘教版（2019）必修 第一册6.4 用样本估计总体图片ppt课件，共42页。PPT课件主要包含了内容索引，课前篇自主预习，课堂篇探究学习，情境导入，知识梳理，答案D，答案C，答案26等内容，欢迎下载使用。

1.结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差).(数据分析、数学运算)2.理解离散程度参数的含义.(数学抽象)
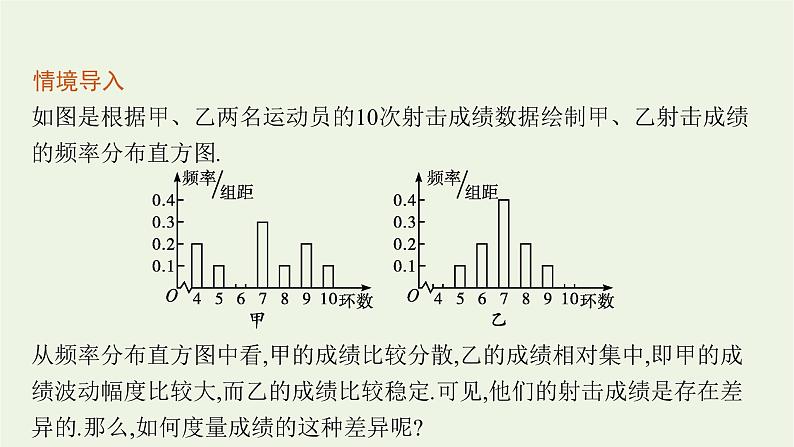
如图是根据甲、乙两名运动员的10次射击成绩数据绘制甲、乙射击成绩的频率分布直方图.
从频率分布直方图中看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在差异的.那么,如何度量成绩的这种差异呢?
知识点一:极值与极差
一组数据中的最大值与最小值统称为极值,最大值与最小值之差称为极差,也称全距,用R表示.
是数据中的值,但可能各有多个
要点笔记极差反映了一组数据变化的幅度,是描述数据离散程度最简单的代表值,容易受极端值的影响.
微练习某个比赛的计分规则为:当评委亮分后,其成绩先去掉一个最高分,再去掉一个最低分,然后计算剩下分数的平均值.这是为了(　　)A.减少计算量B.避免故障C.剔除异常值D.活跃赛场气氛答案 C解析 因为该比赛的评分中使用的是平均分,记分过程中采用“去掉一个最高分,去掉一个最低分”的方法,就是为了防止个别裁判的人为因素给出过高或过低的分数对选手的得分造成较大的影响,从而降低误差,尽量公平.
知识点二:方差与标准差
3.标准差:方差的算术平方根称为标准差.
4.方差的性质:如果a,b是常数,s为x1,x2,…,xn的方差,则ax1+b,ax2+b,…,axn+b的方差为a2s2.
名师点析 应用标准差及方差的注意点(1)标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.
(3)因为方差与原始数据的单位不同,且平方后可能夸大了偏差的程度,所以虽然方差与标准差在刻画样本数据的离散程度上是一样的,但在解决实际问题时,一般采用标准差.(4)当样本的容量和总体的容量相等时样本的方差和总体的方差也相等.
微练习一组数据1,-1,0,-1,1的方差和标准差分别是(　　)A.0,0　　　　 B.0.8,0.64
微思考一组观测数据的标准差、方差是0时,数据有什么特征?提示 标准差、方差为0时,各数据相等,说明数据没有波动幅度,数据没有离散性.
A.8B.4C.2D.1(2)甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:吨/公顷)如下:
则甲、乙两种水稻产量的极差分别为　　　　、　　　　. 
(3)(2019江苏高考)已知一组数据6,7,8,8,9,10,则该组数据的方差是　　　　　(用分数表示). 分析(1)若变量x的方差为s2,变量y满足y=ax+b,则变量y的方差为a2s2;(2)依据极差的定义求值;(3)首先求得平均数,然后求解方差即可.
延伸探究在本例(3)的数据中增加一个数“8”,方差是多少?与原数据的方差相比有什么变化?
变式训练1(1)某校举行了一次知识竞赛,满分10分,有10名同学代表班级参加比赛,已知学生得分均为整数,比赛结束后统计这10名同学得分情况如折线统计图所示,则这10名同学成绩的极差为　　　　　. 
(2)(2021山东青岛第一中学高一期中)某人任意统计5次上班步行到单位所花的时间(单位:分钟)分别为8,12,10,11,9,则这组数据的标准差为　　　　　. 
解析 (1)由题意知数据3,6,6,6,6,6,7,8,9,10的极差是10-3=7.(2)由题意得,这组数据的平均数
例2为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,高一(11)班准备从甲、乙两位同学中选出一人参加学校的比赛,甲、乙两人近期8次汉字听写训练成绩如下所示:甲:68,69,71,72,74,78,85,83;乙:65,70,70,73,75,80,82,85.(1)求甲、乙两人成绩的平均数;(2)现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
∴两人的平均成绩相等,但甲的成绩比较稳定,故派甲参加比较合适.
反思感悟 标准差(方差)的两个作用(1)判断数据的离散程度.标准差(方差)较大,说明数据的离散程度较大;标准差(方差)较小,说明数据的离散程度较小.(2)在实际应用中,常常把平均数与方差或标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差来确定稳定性.
变式训练2甲、乙两台机床同时生产一种零件,在10天中,两台机床每天生产的次品数分别为:甲:0,0,1,2,0,0,3,0,4,0;乙:2,0,2,0,2,0,2,0,2,0.根据两组数据平均数和标准差的计算结果比较两台机床的性能.
例3甲、乙两支田径队体检结果为:甲队的体重的平均数为60 kg,方差为200,乙队体重的平均数为70 kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,试计算甲、乙两队全部队员的平均体重和方差.分析根据题意计算出甲、乙两队队员所占的比例,然后根据甲、乙两队的平均体重计算出总体的平均体重,结合方差计算公式求总体的方差.
反思感悟 计算分层抽样的方差s2的步骤(以2层为例)
解析 由图可知,甲同学除第二次考试成绩略低于乙同学,其他五次考试都远高于乙同学,可知 ,图中数据显示甲同学的成绩比乙同学稳定,故σ甲<σ乙.故选C.
方法点睛由于统计图表反映了样本数据的取值与分布规律,而一组数据的方差与标准差反映了一组数据的离散与波动程度,因此样本数据方差或标准差较小的表现在图表上则更集中,波动性小,方差或标准差较大的表现在图表上则更分散,波动性大.
1.(多选题)下列说法正确的是(　　)A.方差是标准差的平方B.标准差的大小不会超过极差C.若一组数据的值大小相等,没有波动变化,则标准差为0D.标准差越大,表明各个样本数据在样本平均数周围越集中;标准差越小,表明各个样本数据在样本平均数周围越分散答案 ABC解析 标准差越小,表明各个样本数据在样本平均数周围越集中;标准差越大,表明各个样本数据在样本平均数的周围越分散.
2.在一次“爱心互助”捐款活动中,高一某班第一小组8名同学捐款的金额(单位:元)如下表所示:
则这8名同学捐款金额的极差是(　　)A.10B.3C.5D.7
答案 C解析 这8名同学捐款金额的最大值为10,最小值为5,因此极差是5.
3.射击队要从甲、乙、丙、丁四名队员中选出一名选手去参加射击比赛,四人的平均成绩和方差如下表,根据表格中数据判断,参赛最为合适的是(　　)
A.甲B.乙C.丙D.丁
答案 C解析 由表可知,丙的平均成绩较高,且发挥比较稳定,应派丙去参赛最合适.
4.一组数据的方差是4,将这组数据中的每个数据都乘5,所得到的新数据的标准差是　　　　. 答案 10解析 新数据的方差为52×4=100,因此标准差是10.
5.在高一期中考试中,甲、乙两个班的数学成绩统计如下表: