人教版八年级上册13.3.2 等边三角形背景图ppt课件

这是一份人教版八年级上册13.3.2 等边三角形背景图ppt课件，共24页。PPT课件主要包含了你了解它们吗，等边三角形，探索新知，等边三角形性质定理，Why，小组活动2，思考思考，练习1，想一想，教师寄语等内容，欢迎下载使用。

1、关于等边三角形你已经知道了哪些知识？2、你还相知道些什么？
知识与技能 1．了解等边三角形是特殊的等腰三角形，等边 三角形是轴对称图形； 2。 会阐述、推证等边三角形的性质和判定方法能力目标： 经历“猜想—验证—总结归纳—应用”的探究过程， 采用自主探索与合作交流的方式,亲历“做数学”的 过程，培养探究 数学问题、解决问题的能力情感目标： 1． 体验数学充满着探索与创造，感受数学的严谨性，对数学产生强烈的好奇心和求知欲。 2． 在学习中获得成功的体验,感受到数学学习的乐趣, 建立自信心。 3． 体会数学源于生活而又反作用于生活,培养用数学的意识
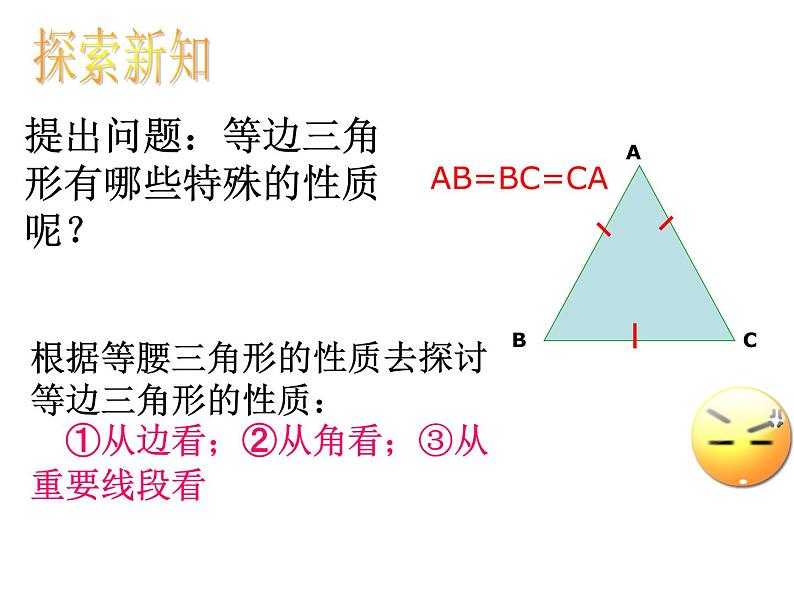
提出问题：等边三角形有哪些特殊的性质呢？
根据等腰三角形的性质去探讨等边三角形的性质：　①从边看；②从角看；③从重要线段看
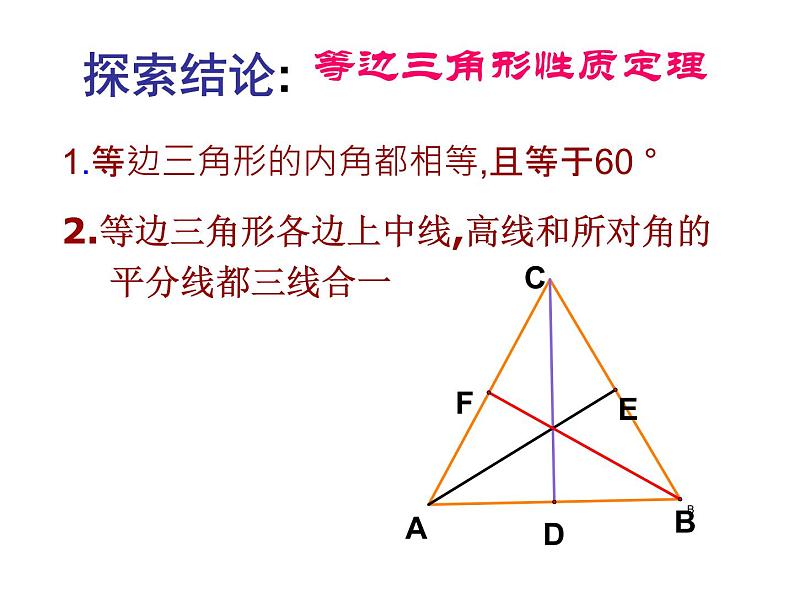
1.等边三角形的内角都相等,且等于60 °
2.等边三角形各边上中线,高线和所对角的 平分线都三线合一
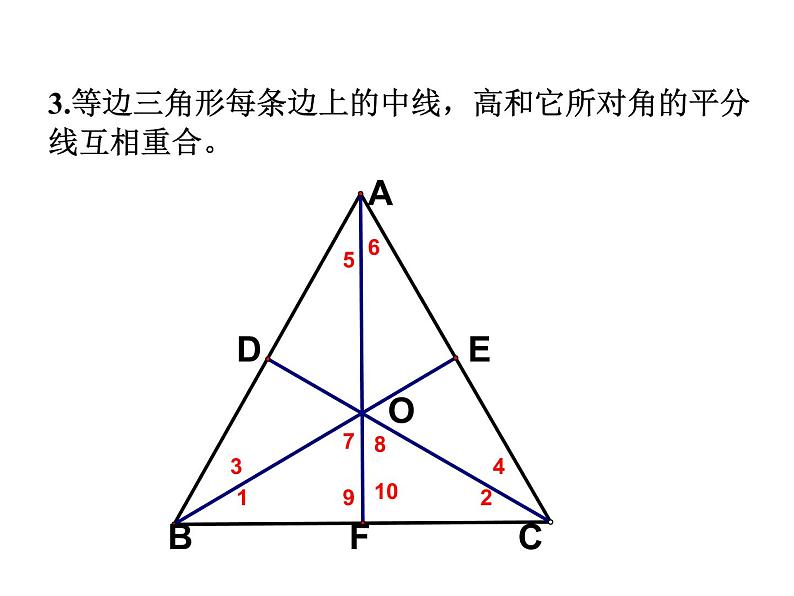
3.等边三角形每条边上的中线，高和它所对角的平分线互相重合。
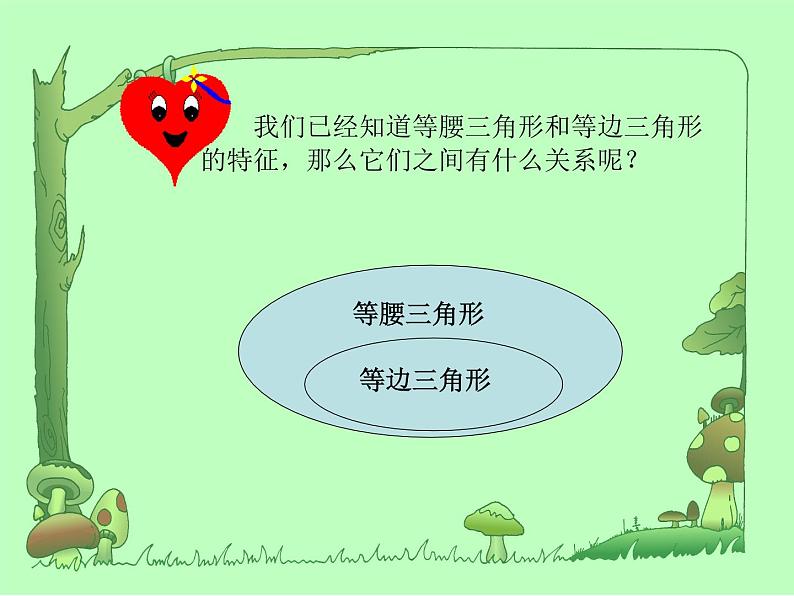
我们已经知道等腰三角形和等边三角形的特征，那么它们之间有什么关系呢？
怎样判断三角形ABC是等边三角形？
方法一：三角形的三边相等；
方法三：有一个角等于60°的等腰三角形是等边三角形。
方法二：三角形的三角相等；
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.2.三个内角都等于60 °的三角形是等边三角形.3.有一个内角等于60 °的等腰三角形是等边三角形.
(2)若D、E分别 是AB、AC上的中点， (3)△ADE是等边三角形吗？
例2：如图B是AP上一点，△APC、 △BDP都是等边三角形，联结BC和DP.图中隐藏着一对全等三角形，你能找出他们吗？(1)试着说明道理
2.如图，等边三角形ＡＢＣ中，ＡＤ是ＢＣ上的高， ∠ ＢＤＥ＝∠ＣＤＦ＝６０ °，图中有哪些与BD相等的线段？
与BD相等的线段有：DC、FC、FD、BE、DE、AE、AF
1、用等边三角形能拼出如图的正六边形吗？2、能用等边三角形的瓷砖来铺设地面吗？
1.三边都相等的三角形叫做____三角形.2.等边三角形的每个内角都等于____度.3.等边三角形有____条对称轴.
4、已知△ABC中，∠A=∠B=60°，AB=3cm 则△ABC的周长________
5、 △ABC是等腰三角形，周长为15cm且∠A=60°，则BC=_______
等边三角形是一种特殊的等腰三角形，你能述说等边三角形与等腰三角形在定义，性质和判定的异同吗?
1、两边、两角相等2、三线合一3、一条对称轴
1、三边、三角相等2、三线合一3、三条对称轴
1、定义2、等角对等边
1、定义2、三个角都相等3、等腰三角形有一个角是600
1、△ABC是等边三角形，以下三种分法分别得到的△ADE是等边三角形吗，为什么？ ①在边AB、AC上分别截取AD＝AE.
②作∠ADE＝600，D、E分别在边AB、AC上.
③过边AB上一点D作DE∥BC，交边AC于E点.
证明：∵△ABC是等边三角形∴∠A=∠B=∠C=600又∵DE∥BC∴∠ADE=∠B，∠AED=∠C ∴∠ADE=∠A=∠AED∴△ADE是等边三角形。
1、△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD, 求证:BD=DE
小试牛刀：(书本P66 第14题)
2．已知：如图，P、Q是△ABC的边BC上的两点，并PB=PQ=QC=AP=AQ,求∠BAC的大小．
3、如图，已知△ABC是等边三角形，P是BC上一点，问在CA和AB上是否存在点Q和R，使△PQR为等边三角形？若存在，求出点Q和R，并加以证明；若不存在。请说明理由.
课外活动小组在一次测量活动中,测得∠APB＝60°AP＝BP＝200m,他们便得到了一个结论:池塘最长处不小于200m.他们的结论对吗?
∵AP=BP=200m，∠APB= 60°∴AB＝AP＝PB=200m
从而△APB是等边三角形，AB的长是200m,由此可以得出兴趣小组的结论是正确的。
愿你用勤奋的汗水浇灌智慧的花朵
2、如图， △ABC中，D、E是BC边上的三等分点， △AED是等边三角形，则∠BAC为（　　　　）度？3、在△ABC中，AB=AC，以AB、AC为边在△ABC的外侧作两个等边三角形△ABE和△ACD，且∠EDC=40°，则∠ABC＝（　　　）度？