


初中数学人教版八年级上册13.2.1 作轴对称图形教案配套课件ppt
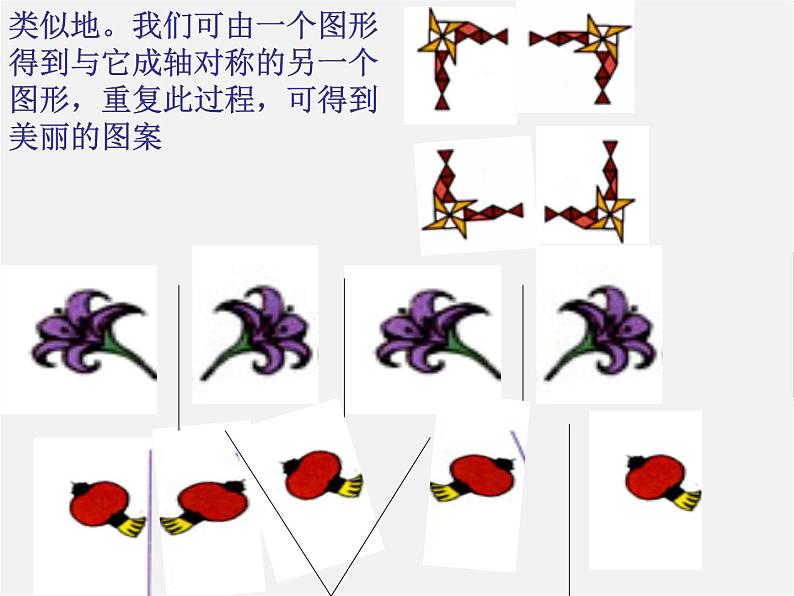
展开类似地。我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案
由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点,都是原图形上的某一点关于直线L的对称点;
连接任意一 对对于的对应点的线段被对称轴垂直平分。
如果有一 个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?
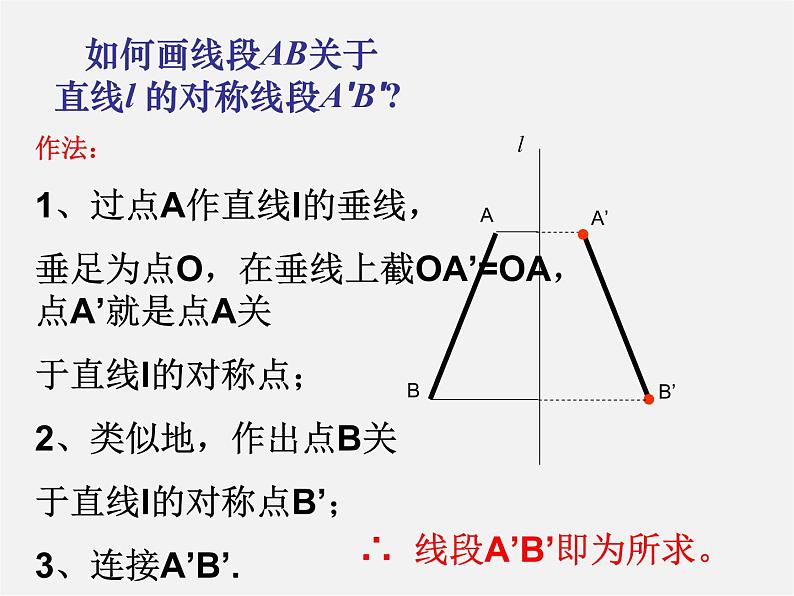
如何画线段AB关于直线l 的对称线段A′B′?
作法:1、过点A作直线l的垂线,垂足为点O,在垂线上截OA’=OA,点A’就是点A关于直线l的对称点;2、类似地,作出点B关于直线l的对称点B’;3、连接A’B’.
∴ 线段A’B’即为所求。
1、过点A作直线l的垂线,垂足为点O,
在垂线上截取OA’=OA,
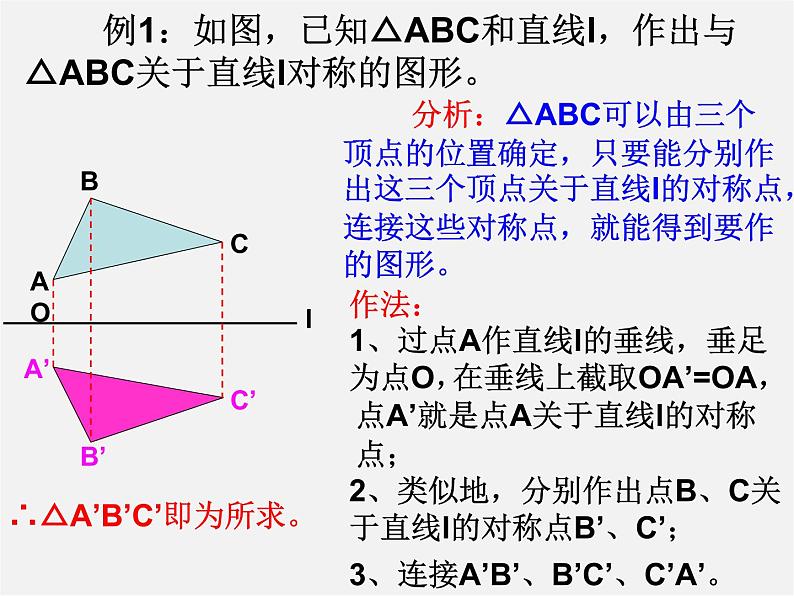
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求。
点A’就是点A关于直线l的对称点;
我行了:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
∴△AB’C’即为所求。
1、分别作出点B、C关于直线l的对称点B’、C’;
2、连接AB’、B’C’、C’A。
1、分别作出点A、B关于直线l的对称点A’、B’;
2、连接A’B’、B’C、CA’。
∴△A’B’C即为所求。
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形;
对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接对称点,就可以得到原图形的轴对称图形。
利用轴对称,可以设计出精美的图案。请你用所学的知识来欣赏下列美丽的图案
要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在L上找几个点试一试,能发现什么规律吗?
初中数学人教版八年级上册13.2.1 作轴对称图形一等奖课件ppt: 这是一份初中数学人教版八年级上册13.2.1 作轴对称图形一等奖课件ppt,共50页。PPT课件主要包含了教学目标,教学重点,教学难点,都是轴对称图形,关于对称轴对称即可,成轴对称,折痕垂直平分PP,完全相同,对称点,垂直平分等内容,欢迎下载使用。
人教版13.2.1 作轴对称图形教案配套课件ppt: 这是一份人教版13.2.1 作轴对称图形教案配套课件ppt,共15页。PPT课件主要包含了轴对称变换,两点之间线段最短等内容,欢迎下载使用。
数学八年级上册13.2.1 作轴对称图形习题课件ppt: 这是一份数学八年级上册13.2.1 作轴对称图形习题课件ppt,共16页。













