人教版八年级上册14.1.2 幂的乘方教学演示ppt课件

这是一份人教版八年级上册14.1.2 幂的乘方教学演示ppt课件，共39页。PPT课件主要包含了同底数幂相乘，同底数幂的乘法公式，同底数幂的乘法逆用，amn，anm，abn，anbn，幂的乘方公式，mn都是正整数，化为同指数后比较等内容，欢迎下载使用。

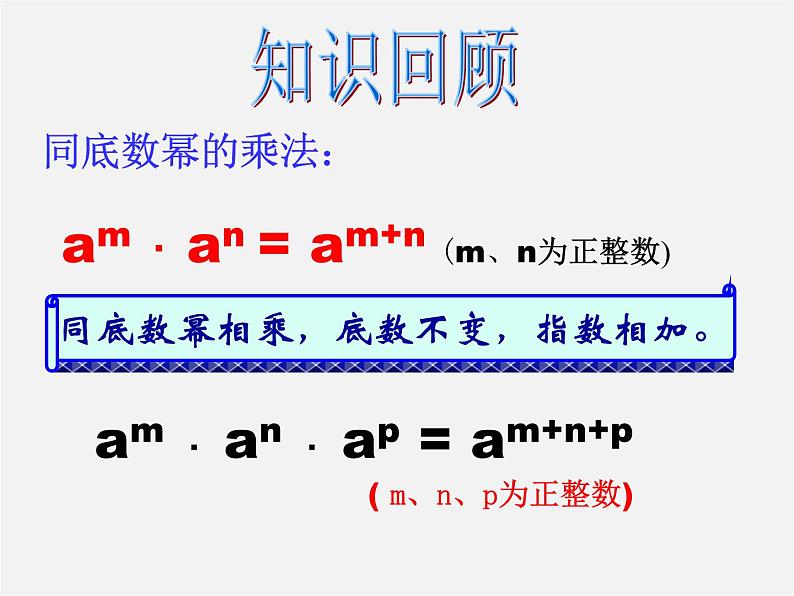
am · an = am+n(m、n都是正整数)
底数　　 ，指数　　 。
am+n = am · an (m、n都是正整数)
(m,n都是正整数).
单项式与单项式相乘，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。
单项式与单项式相乘的法则：
1、下列计算中，正确的是（ ）A、2a3·3a2=6a6 B、4x3·2x5=8x8C、2X·2X5=4X5 D、5X3·4X4=9X7
2、下列运算正确的是（ ）A、X2·X3=X6 B、X2+X2=2X4C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
① a · a2＝ a2 　 ② a＋a2 ＝ a3 ③ a3 · a3＝ a9 　 ④ a3＋a3 ＝ a6
判断下列计算是否正确，并简要说明理由：
(1)x4·x6=x24 ( 　) (2) x·x3=x3 ( 　) (3) x4+x4=x8 (　 ) (4)x2·x2=2x4 (　 ) (5)a2·a3 - a3·a2 = 0 ( 　 ) (6)x3·y5=(xy)8 ( 　 ) (7) x7+x7=x14 ( 　 )
判断（正确的打“√”，错误的打“×”）
底数 　　，指数 　　。
（1）　　　　　　　　　　　　（　　）
（2）　　　　　　　　　　　　（　　）
（3）　　　　　　　　　　　　（　　）
（4）　　　　　　　　　　　　（　　）
（5）　　　　　　　　　　　　（　　）
（6） 　　　　　　　　　　　　 （ ）
在255，344，433，522这四个幂中，数值最大的一个是———。
解：255=25×11=(25)11=3211
344=34×11=(34)11=8111
433=43×11=(43)11=6411
522=52×11=(52)11=2511
深入探索----议一议2
（4）比较375，2100的大小
解：∵ 375=33×25=(33)25=2725
2100=24×25=(24)25=1625
且 16＜27 ∴1625＜2725 即2100＜375
（5）比较1625，290的大小
解：∵ 1625=(24)25=2100
且 90＜100∴290＜2100 即290＜1625
（6）已知a=166，b=88 c=412 ，比较a，b，c的大小
解：∵ 166=(24)6=224
88=(23)8=224
412=(22)12=224
∴a=b=c
（7）已知2a=3，2b=6，2c=12 ，则a，b，c的关系
解：∵ 62=12×3
∴(2b)2=2a · 2c
（1）已知2x+5y-3=0, 求 4x · 32y的值
（2）已知 2x =a， 2y =b， 求 22x+3y 的值
（3）已知 22n+1 + 4n =48， 求 n 的值
（5）若(9n)2 = 38 ， 则n为______
判断下面计算是否正确，如有错误请改正。
所以数值最大的一个是______
1、了解幂的乘方的运算法则。 2、了解积的乘方的运算法则，并能灵活运用3种法则。
面积S= .
面积S= .
能不能快速说出是几个3相乘
体积V= .
你能说出各式的底和指数吗？
（3）
这几道题有什么共同的特点呢?计算的结果有什么规律吗?
（1）
（2）
(1) (103)5 (2) (a4)4(3) (am)2 (4) -(x4)3
幂的乘方的逆运算：(1)x13·x7=x（ ）=( )5=( )4=( )10； (2)a2m =( )2 =( )m （m为正整数）.
判断下列计算是否正确，如有错误请改正。
(2) a6 · a4 = a24
(x3)3 = x6
⑵(a-b)3［(a-b)3］2
⑶［(x-y)2］2［(y-x)2］3
今天，我们学到了什么？
2. 已知3×9n=37，求：n的值．
1. 已知53n=25，求：n的值．
多重乘方也具有这一性质