人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定背景图课件ppt

这是一份人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定背景图课件ppt，共20页。PPT课件主要包含了平行线的画法，直线平行的条件，双基检测，想一想等内容，欢迎下载使用。
学习目标 1、运用平行线的画法对平行线的判定方法进行推导 2、学习平行线的判定方法的相关内容 3、会正确运用平行线的判定方法对两条直线的位置关系进行判定即平行线判定的简单运用
1、两条直线的位置关系有哪几种？
2、怎样的两条直线平行？
3、平行线的公理及推论是什么？
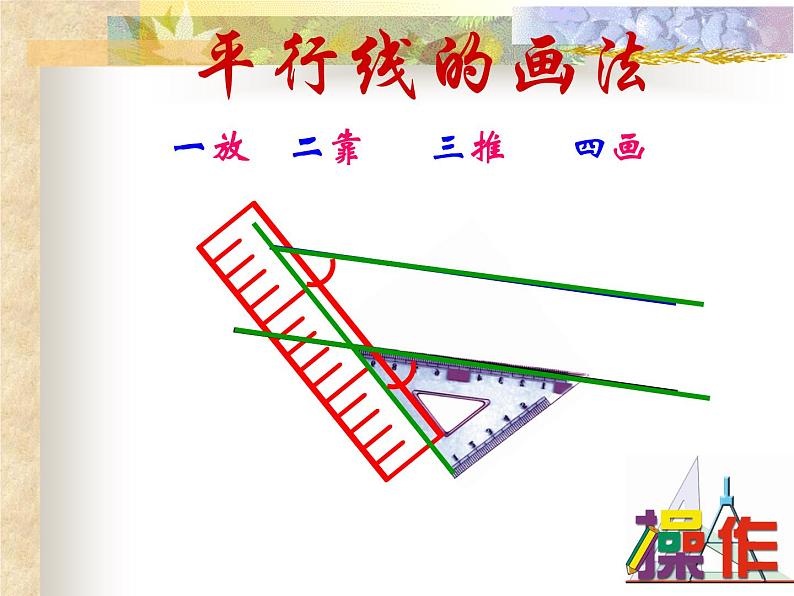
自学指导合作探究 学生运用5分钟的时间自学13页、14页的内容，并思考如下问题： 1、平行线的判定方法一的内容是什么？ 2、平行线的判定方法二的内容是什么？ 3、平行线的判定方法三的内容是什么？ 4、你知道平行线的这些判定方法是怎样推导出来的吗？
从画图过程，三角板起到什么作用？
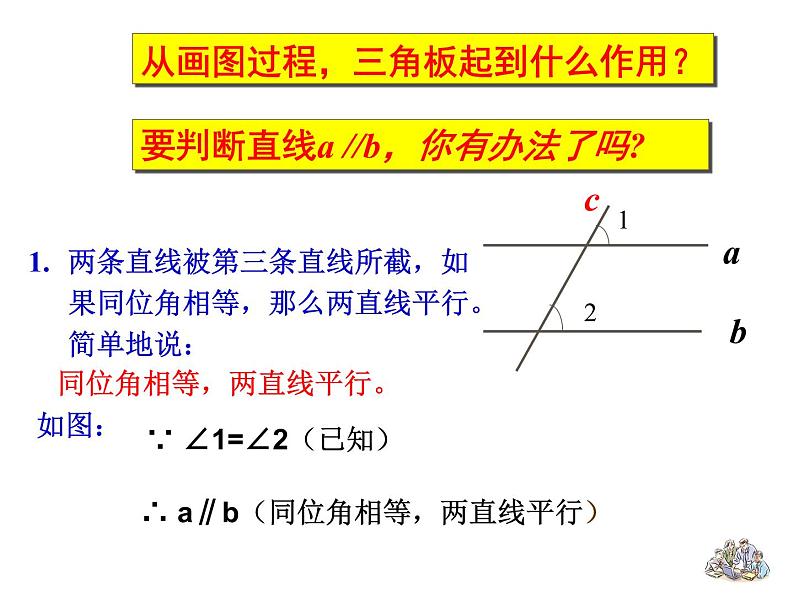
要判断直线a //b，你有办法了吗?
两条直线被第三条直线所截，如果同位角相等，那么两直线平行。简单地说： 同位角相等，两直线平行。
∵ ∠1=∠2（已知）
∴ a∥b（同位角相等，两直线平行）
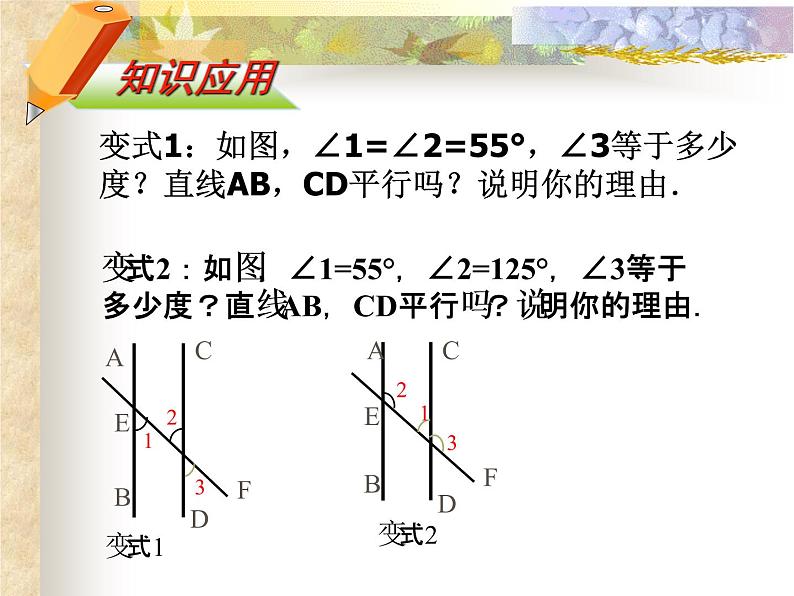
１．如图，∠1=∠2=55°，∠3等于多少度？直线AB，CD平行吗？说明你的理由．
变式1：如图，∠1=∠2=55°，∠3等于多少度？直线AB，CD平行吗？说明你的理由．
① 如图： 如果∠1=∠３， 那么a与b平行吗？
内错角相等，两直线平行。
② 如图： 如果∠1+∠2=180， 那么a与b平行吗？
同旁内角互补，两直线平行。
同位角相等，两直线平行。
1.如果∠A＝∠3，那么　 ∥ , （　 ）2.如果∠2＝∠E，那么　 ∥ ,　　（　 ）3.如果∠A+∠ABE＝1800，那么 ∥ ,　（　　　　 ）4.如果∠2＝　　，那么DA∥EB（　　　　　　 ）5.如果∠DBC＋　 ＝1800，那么DB∥EC（　　　　　　 ）
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
① ∵ ∠2 =___（已知） ∴ ___∥___
② ∵ ∠3 = ∠5（已知） ∴ ___∥___
③∵ ∠4 +___=180（已知） ∴ ___∥___
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
１．找出下图互相平行的直线
２.已知∠3=45 °，∠1与∠2互余，试说明 ？
解：∵∠1=∠2（对顶角相等） ∠1+∠2=90°(已知) ∴∠1=∠2=45° ∵ ∠3=45°(已知) ∴∠ 2=∠3 ∴ AB∥CD(内错角相等，两直线平行)
3. 如图：已知 ∠1=75 , ∠2 =105 问：AB与CD平行吗？为什么？
“在同一平面内，垂直于同一条直线的两条直线互相平行”是否可以看做平行线判定方法的特殊情形？
如图：已知ABCD，ABEF，那么CD//EF吗？
1．如图所示：(1)如果已知∠1=∠3，则可判定AB∥______,其理由是__________________;(2)如果已知∠4+∠5=180°，则可判定___________∥______,其理由是__________________;(3)如果已知∠1+∠2=180°，则可判定___________∥______,其理由是__________________;(4)如果已知∠5+∠2=180°那么根据对顶角相等有∠2=__,因此可知∠4+∠5= ____,所以可确定 ___________∥______,其理由是__________________; (5)如果已知∠1=∠6，则可判定_____∥______,其理由是__________________.