





初中数学浙教版八年级上册2.7 探索勾股定理课堂教学课件ppt
展开(1)直角三角形的两直角边为3和4,则斜边为___
(3)直角三角形的两直角边为6和8,则斜边为___
(2)直角三角形的两直角边为5和12,则斜边为___
(5)直角三角形的两条边为3和4,则斜边上的高是 。
(4)直角三角形的两条边为3和4,则这个直角三角形的第三边长为 。
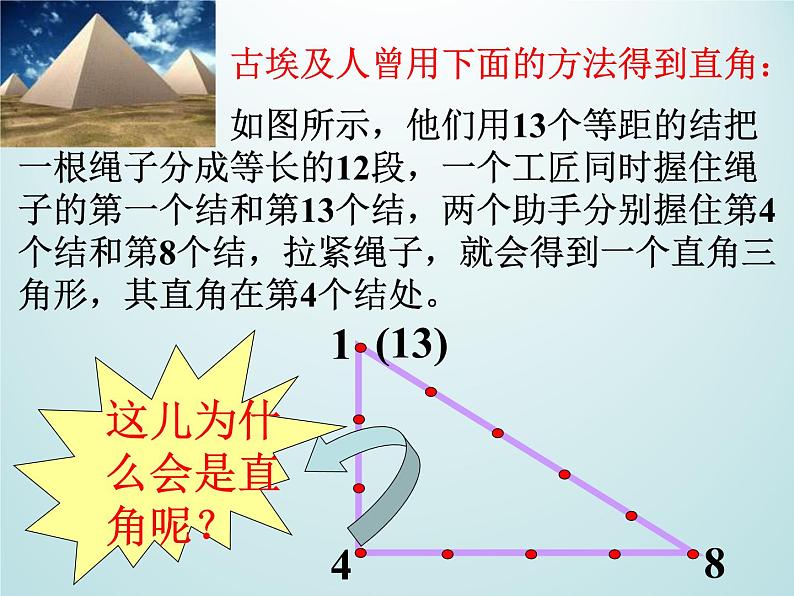
古埃及人曾用下面的方法得到直角: 如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
一、画一个三角形,使其三边长(a<b<c)分别为:
(1)5cm, 12cm, 13cm;(2) 3cm, 4cm, 5cm ;(3)1.5cm, 2cm, 2.5cm;
二、再用量角器量一量最大的角,判断它们是否是直角三角形?
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a,b,c有关系
1.想一想:上述哪条边所对的角是直角?
2.能够满足a2+b2=c2的三个正整数叫做一组勾股数(或勾股弦数)。 如3、4、5; 6、8、10; 5、12、13。
由此你得到怎样的结论?
1.若一个三角形的三边满足a2-b2=c2 ,则这个三角形为( )A:直角三角形 B:正三角形 C:锐角三角形 D:钝角三角形2.在△ABC中BC=a,AC=b,AB=c,且b2+c2=a2, 则∠ =90°
例1 根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形(1)a=7,b=24,c=25(2)a= b=1,c=
根据下列条件,判断下面以a、b、c 为边的三角形是不是直角三角形(1) a=20,b=21,c=2(2)
例2、已知△ABC三条边长分别为a,b,c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)。△ABC是直角三角形吗?请说明理由.
解:∵ a=m2-n2,b=2mn,c=m2+n2
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4
∴△ABC是直角三角形
例3、如图,在四边形ABCD中,AB=3,BC=4, CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=4,BC=3, CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
直角三角形两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
直角三角形的判定方法之一:
如图在△ABC中AB=4,BC=2,BD=1,CD= 判断下列结论是否正确,并说明理由(1) CD ⊥AB; (2) AC⊥BC
解(1)∵BC2=BD2 +CD2=4
(2)∵AC2=AD2+CD2=12
AC2+BC2=16=AB2
已知△ABC的三条边长分别为a、b、c,且满足关系:2b(c+2b)+(2c+a)(2c-a)=3(b+c)2-4bc ,试判断△ABC的形状,并说明理由.
已知△ABC的三条边长分别为a、b、c,且满足关系: (a+b)2 + c2 = 3ab + c(a+b), 试判断△ABC的形状,并说明理由.
初中浙教版2.7 探索勾股定理课前预习ppt课件: 这是一份初中浙教版2.7 探索勾股定理课前预习ppt课件,共17页。PPT课件主要包含了勾股定理,勾股定理的逆定理,直角三角形的判定方法,合作探究等内容,欢迎下载使用。
数学八年级上册2.7 探索勾股定理课文内容课件ppt: 这是一份数学八年级上册2.7 探索勾股定理课文内容课件ppt,共25页。PPT课件主要包含了∴a2+b2c2,a+b2,c2+,也可以表示为,a2+b2c2,它们之间的关系是,化简得,勾股定理,+x2172,+122x2等内容,欢迎下载使用。
初中数学浙教版八年级上册2.7 探索勾股定理授课课件ppt: 这是一份初中数学浙教版八年级上册2.7 探索勾股定理授课课件ppt,共14页。PPT课件主要包含了勾股小知识,小结归纳,回顾与小结,这节课你有什么收获等内容,欢迎下载使用。













