初中浙教版2.7 探索勾股定理课前预习ppt课件

这是一份初中浙教版2.7 探索勾股定理课前预习ppt课件，共17页。PPT课件主要包含了勾股定理，勾股定理的逆定理，直角三角形的判定方法，合作探究等内容，欢迎下载使用。

1、若c为直角△ABC的斜边，b、a为直角边， 则a、b、c的关系为_____________2、
直角三角形两条直角边的平方和等于斜边的平方
直角三角形的一直角边和斜边长分别为5和13,则其另一直角边长为_________.
你能说出勾股定理的逆命题吗？下面我们一起来探索这个逆命题
（1）作一个三角形,使其三边长分别为:3cm，4cm,5cm； 1.5cm，2cm,2.5cm;5cm,12cm,13cm
（3）量一量所作每一个三角形最大边所对角的度数。
由此你得到怎样的结论?
（2）算一算较短两条边的平方和与最长一条边的平方是否相等
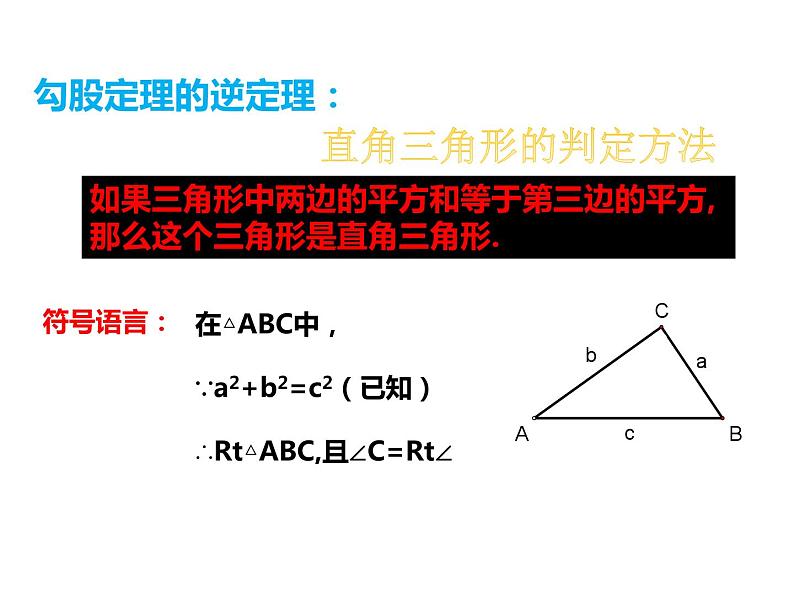
如果三角形中两边的平方和等于第三边的平方，那么这个三角形是直角三角形。
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
在△ABC中，∵a2+b2=c2（已知） ∴Rt△ABC,且∠C=Rt∠
利用勾股定理逆定理判断是否为直角三角形的方法：
1.区分最长边与较短两边，2.比较较短两边的平方和与最长边的平方，3.若相等，则三角形是直角三角形，并且最长边所对的角是直角; 否则该三角形不是直角三角形
例4.已知△ABC三条边长分别为a,b,c,且a＝m2－n2，b＝2mn，c＝m2＋n2(m>n，m,n是正整数)。△ABC是直角三角形吗？请证明你的判断。
∵ a=m2－n2，b=2mn，c＝m2＋n2 （m>n，m，n是正整数）
∴ a2+b2=(m2－n2)2+(2mn)2
＝m4－2m2n2＋n4＋4m2n2
＝m4＋2m2n2＋n4
∴△ABC是直角三角形（__________________________）
解：△ABC是直角三角形，证明如下：
1.如图，明明散步从A到B走了41米，从B到C走了40米，从A到C走了9米，则∠A+∠B的度数是______度．
解：∵从A到B走了41米，从B到C走了40米，从A到C走了9米， ∴AB=41，BC=40，AC=9， 由勾股定理的逆定理得：412=402+92， ∴△ACB是直角三角形，AB是斜边， ∴∠A+∠B=90°．
2.如图所示，BD=4，AD=3，∠ADB=90°，BC=13，AC=12，求阴影部分的面积．
3.如图，分别以三角形三边为直径向外作三个半圆，如果较小的两个半圆面积之和等于较大的半圆面积． 求证：这个三角形是直角三角形．
如图,以△ABC的每一条边为边作三个正方形.已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请证明你的判断.
观察下列勾股数组：3，4，5；5，12，13；7，24，25；9，40，41；…a、b、c．你能发现什么规律，根据你发现的规律，请写出： （1）当a=19时，则b、c的值是多少（2）当a=2n+1时，求b、c的值．你能证明所发现的规律吗．
解：（1）当a=19时，设b=k，则c=k+1，观察有如下规律：192+k2=（k+1）2，k=180，故b=180，c=181．
（2）当a=2n+1时，设b=k，则c=k+1，根据勾股定理：a2+b2=c2，即（2n+1）2+k2=（k+1）2解得k=2n（n+1），即b=2n（n+1）， c=2n（n+1）+1． 证明：a2+b2=（2n+1）2+[2n（n+1）]2=4n4+8n3+8n2+4n+1，[2n（n+1）+1]2=4n4+8n3+8n2+4n+1，所以a2+b2=c2， 所以a、b、c组成的三角形是直角三角形．