数学13.3.1 等腰三角形教学演示ppt课件

这是一份数学13.3.1 等腰三角形教学演示ppt课件，共22页。

1、理解并掌握等腰三角形的性质；
2、经历等腰三角形的性质的探究过程，能初步运用等腰三角形的性质解决有关问题；
3、培养分类讨论、方程的思想和添加辅助线解决问题的能力.
1.等腰三角形的周长是35cm，腰长是底边的2倍，则该三角形的底边长是________cm，腰长是__________cm。2.等腰三角形的两边长分别为8cm和6cm，那么它的周长为（ ） A、20cm B、22cm C、20cm或22cm D、都不对3.已知等腰三角形的一个外角等于70°，那么底角的度数是（ ）A、110° B、55° C、35° D、以上都不对4.已知等腰三角形的一个外角等于130°，那么底角的度数是（ ）A、50° B、65° C、50°或65° D、以上都不对
探究点一问题1：如下图，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的三角形有什么特点？操作结论：剪刀剪过的两条边_______，即△ABC中的边____=_____，所以得到的三角形是_______三角形。等腰三角形的定义：有_________相等的三角形是等腰三角形等腰三角形中相等的两边叫做________，另一边叫做_________，两腰所夹 的角叫做_________，底边与腰的夹角叫__________。
探究点一问题2：如图，把剪出的三角形ABC沿折痕对折，找出其中重合的线段与角，由这些重合的线段与角，你能发现等腰三角形的性质吗？重合的角 ，重合的线段 . 1、通过操作可以得到等腰三角形的以下性质：性质1 等腰三角形的两个_______相等（简写“等边对等_____”）数学符号表示：在△ABC中，∵AB=AC ∴∠_____=∠_____
B C
探究点一问题2：如图，把剪出的三角形ABC沿折痕对折，找出其中重合的线段与角，由这些重合的线段与角，你能发现等腰三角形的性质吗？性质2 等腰三角形的顶角_______线、底边上的_____线、底边上的_____相互重合（简写成“三线合一”）（1）等腰三角形底边上的高AD，既是底边上的 ，又是顶角 ；即在等腰△ABC中，AB=AC，∵AD⊥BC，∴____= ____，∠_____ = ∠_____ ；
BAD CAD
（2）等腰三角形的底边上中线AD，既是底边上的 ，又是顶角 . 即在等腰△ABC中，AB=AC，∵AD是中线，∴____⊥____ ，∠_____ =∠_____；（3）等腰三角形的顶角的平分线AD，既是底边上的 ，又是底边上的 ，即在等腰△ABC中，AB=AC，∵AD是角平分线，∴_____ =_____，____ ⊥____ 。
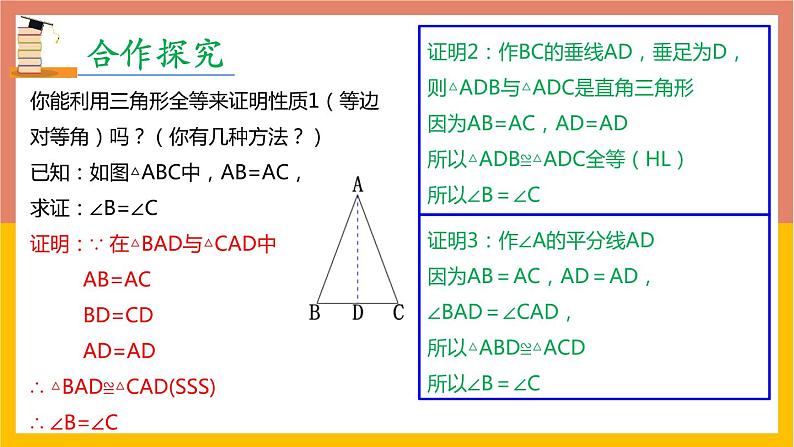
你能利用三角形全等来证明性质1（等边对等角）吗？（你有几种方法？）已知：如图△ABC中，AB=AC，求证：∠B=∠C证明：∵ 在△BAD与△CAD中 AB=AC BD=CD AD=AD∴ △BAD≌△CAD(SSS)∴ ∠B=∠C
证明2：作BC的垂线AD，垂足为D，则△ADB与△ADC是直角三角形因为AB=AC，AD=AD所以△ADB≌△ADC全等（HL）所以∠B＝∠C
证明3：作∠A的平分线AD因为AB＝AC，AD＝AD，∠BAD＝∠CAD，所以△ABD≌△ACD所以∠B＝∠C
探究点二问题2：证明的启发，你能证明性质2（等腰三角形顶角平分线、底边上的中线、底边上的高重合）吗 ?请证之。方法1.已知△ABC中，AB=AC，AD是BC边上的高．求证：BD=CD，∠BAD=∠CAD．证明：因为AD是高，所以∠ADB=∠ADC=90°，因为AB=AC，AD=AD，所以直角△ABD全等直角△ACD,所以BD=CD，∠BAD=∠CAD．
探究点二问题2：证明的启发，你能证明性质2（等腰三角形顶角平分线、底边上的中线、底边上的高重合）吗 ?请证之。方法2.已知△ABC中，AB=AC，AD是BC边的中线，求证：AD⊥BC，∠BAD=∠CAD．因为AB=AC，AD=AD，BD=CD，所以△ABD≌△ACD，所以∠ADB=∠ADC，∠BAD=∠CAD．因为∠ADB+∠ADC=180°，所以∠ADB=90度，即有AD⊥BC．
探究点二问题2：证明的启发，你能证明性质2（等腰三角形顶角平分线、底边上的中线、底边上的高重合）吗 ?请证之。方法3.已知△ABC中，AB=AC，AD平分∠BAC，求证：AD⊥BC，BD=CD．因为AB=AC，∠BAD=∠CAD，AD=AD，所以△ABD≌△ACD，所以∠ADB=∠ADC，BD=CD，因为∠ADB+∠ADC=180°，所以∠ADB=90度，即有AD⊥BC．
例1 如图，△ABC中，AB=AC，点D在AC上，且BD=BC=AD。求△ABC各角的度数解:设∠C=x∵ AB=AC∴ ∠ABC=∠C=x,∠A=180°-2x∵ BD=BC=AD∴ ∠A=∠ABD,∠C=∠BDC=x∵ ∠BDC是△ABD的外角, ∴ ∠BDC=∠A+∠ABD=2∠A即x=360°-4x∴ x=72°则∠ABC=∠C=72°,∠A=36°
例2：如图,在△ABC中,AB=AC,D是BC上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.(1)当点D在BC的什么位置时,DE=DF?请给出证明.(2)过C点作AB边上的高CG,请问DE,DF,CG的长度之间存在怎样的关系?并加以证明.解:(1)当D为BC的中点时,DE=DF.∵D为BC的中点,∴BD=CD,∵AB=AC,∴∠B=∠C,∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,∴△BED≌△CFD(AAS),∴DE=DF.
(2)CG=DE+DF.连接AD,∵S△ABC=S△ADB+S△ADC,∴AB×CG=AB×DE+AC×DF,又AB=AC,∴CG=DE+DF.
1．等腰三角形的一个角是80°，则它顶角的度数是(　 　)A．80° B．80°或20°C．80°或50° D．20°2．如图，在等腰△ABC中，AB＝AC，BD⊥AC，∠ABC＝72°，则∠ABD＝(　 　) A．36° B．54° C．18° D．64°
3．如图，在△ABC中，AB＝AC，∠A＝30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D等于(　 　)　　　　 A．15° B．17.5° C．20° D．22.5°4．如图所示，线段AC的垂直平分线交线段AB于点D，∠A＝50°，则∠BDC＝(　 　) A．50° B．100° C．120° D．130°
5．如图，在△ABC中，AB＝AC，点D，E在BC上，连接AD，AE.如果只添加一个条件使∠DAB＝∠EAC，则添加的条件不能为(　 　)A．BD＝CE B．AD＝AEC．DA＝DE D．BE＝CD6．如图，直线 m∥n ，△ABC 为等腰直角三角形，∠BAC ＝90°，则∠1 ＝_________．7．如图，AC∥BD，AB与CD相交于点O，若AO＝AC，∠A＝48 °，则∠D＝_______．
9．如图，在△ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE＝∠BAD.证明：∵AB=AC，AD是BC边上的中线，BE⊥AC，∴∠CBE+∠C=∠CAD+∠C=90°，∴∠CAD=∠BAD，∴∠CBE=∠BAD．
10．如图，在△ABC中，AB＝AC，AD是角平分线，点E在AD上，请写出图中所有全等的三角形，并选择其中的一对全等三角形加以证明．解：相互全等的三角形有△ABE≌△ACE，△EBD≌△ECD，△ABD≌△ACD以△ABE≌△ACE为例，证明如下：∵ AB=AC∵AD为角平分线，∴ ∠ BAE= ∠ CAE，∵ AE=AE ，∴△ABE≌△ACE（SAS）
1. 等腰三角形的定义2. 等腰三角形的性质：性质1： 等腰三角形的两个底角相等（简写“等边对等角”）性质2： 等腰三角形的顶角平分线、底边上的中线线、底边上的高相互重合（简写成“三线合一”）
书面作业：完成相关书本作业