初中数学北师大版七年级下册4 用尺规作三角形教案

4　用尺规作三角形

教学目标

一、基本目标

1．经历尺规作图实践操作过程，训练和提高学生的尺规作图的技能，能根据条件作出三角形．

2．能依据规范作图语言，作出相应的图形，在实践操作过程中，逐步规范作图语言．

3．通过与同伴交流作图过程和结果的合理性，体会对问题的说明要有理有据．

二、重难点目标

【教学重点】

经历尺规作图的过程，能根据条件作三角形．

【教学难点】

能依据规范作图语言作出相应的图形，在实践操作过程中，逐步规范作图语言．

教学过程

环节1　自学提纲，生成问题

【5 min阅读】

阅读教材P105～P107的内容，完成下面练习．

【3 min反馈】

1．已知三角形的两边及其夹角，作出这个三角形的依据是SAS；已知三角形的两角及其夹边，作出这个三角形的依据是ASA；已知三角形的三条边，作出这个三角形的依据是SSS.

2．下列条件中，用尺规作图不可以作出两个全等三角形的是(　D　)

A．已知三边

B．已知两边及夹角

C．已知两角及夹边

D．已知两边及其中一边的对角

3．已知线段a、b、m，求作△ABC，使BC＝a，AC＝b，BC边上的中线AD＝m.下面作法的合理顺序是③①②.(填序号)

①延长CD到B，使BD＝CD；

②连结AB；

③作△ADC，使DC＝a，AC＝b，AD＝m.

环节2　合作探究，解决问题

活动1　小组讨论(师生互学)

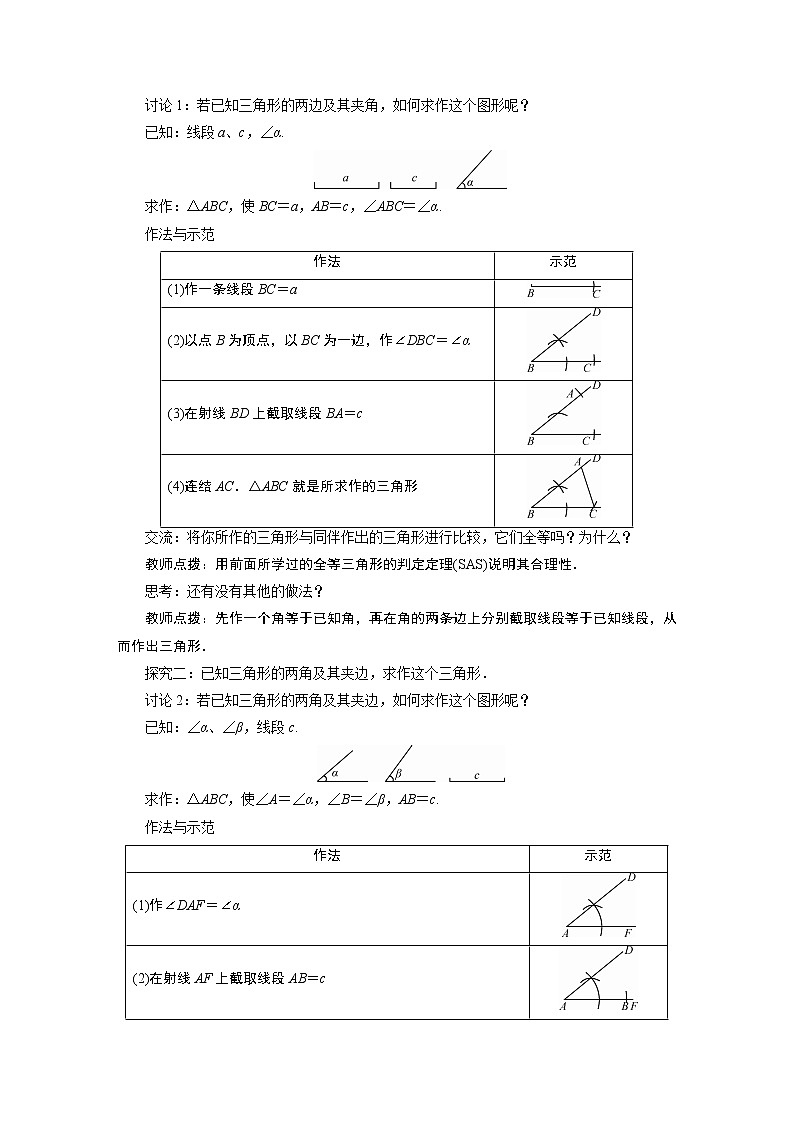
探究一：已知三角形的两边及其夹角，求作这个三角形．

讨论1：若已知三角形的两边及其夹角，如何求作这个图形呢？

已知：线段a、c，∠α.

求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.

作法与示范

交流：将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？

教师点拨：用前面所学过的全等三角形的判定定理(SAS)说明其合理性．

思考：还有没有其他的做法？

教师点拨：先作一个角等于已知角，再在角的两条边上分别截取线段等于已知线段，从而作出三角形．

探究二：已知三角形的两角及其夹边，求作这个三角形．

讨论2：若已知三角形的两角及其夹边，如何求作这个图形呢？

已知：∠α、∠β，线段c.

求作：△ABC，使∠A＝∠α，∠B＝∠β，AB＝c.

作法与示范

交流：将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？

教师点拨：用前面所学过的全等三角形的判定定理(ASA)说明其合理性．

探究三：已知三角形的三条边，求作这个三角形．

讨论3：若已知三边，如何求作一个三角形？

已知：线段a、b、c.

求作：△ABC，使AB＝c，AC＝b，BC＝a.

作法与示范

交流：将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？

教师点拨：用前面所学过的全等三角形的判定定理(SSS)说明其合理性．

活动2　巩固练习(学生独学)

1．完成教材P107“习题4.9”第1～3题．

略

2．如图，已知∠α，线段a，用直尺和圆规求作一个等腰三角形，使得底边为a，底角为∠α.(保留作图痕迹，不必写出作法)

解：如图，△ABC就是所求作的三角形．

教师点拨：先画一底边为a，再从线段的两端分别作两角为α，角的边的交点就是三角形的另一顶点．

环节3　课堂小结，当堂达标

(学生总结，老师点评)

练习设计

请完成本课时对应练习！