初中数学人教版八年级上册12.1 全等三角形课时作业

这是一份初中数学人教版八年级上册12.1 全等三角形课时作业，共8页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
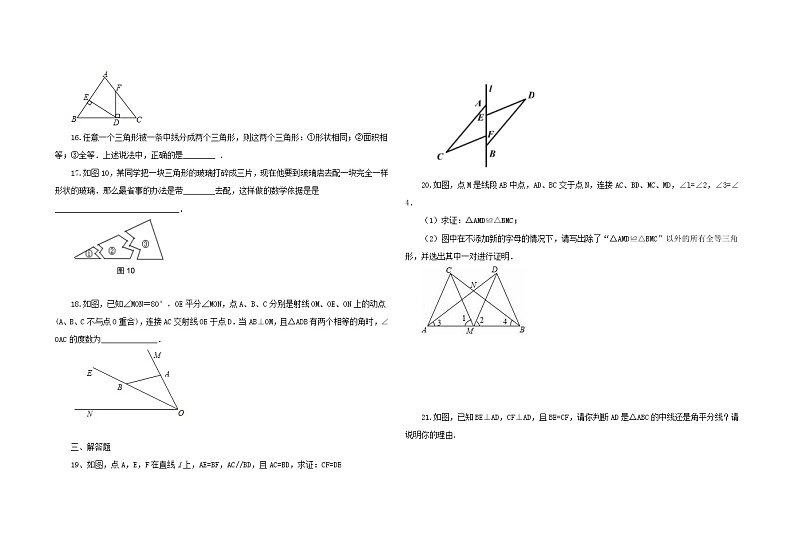
第十二章  全等三角形 单元复习与检测题 A卷（含答案） 一、选择题1、如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（  ）A．AB=DE B．AC=DF C．∠A=∠D D．BF=EC2.已知△ABC≌△DEF，∠A=35°，那么∠D的度数是（     ）A．65° B．55° C．35 D．45°3.如图，小强利用全等三角形的知识测量池塘两端M、N的距离，如果△PQO≌△NMO，则只需测出其长度的线段是（　 　）A．PO B．PQ C．MO D．MQ如图，△ABC≌△ADE，若∠B=70°，∠C=30°，∠DAC=35°，则∠EAC的度数为（　　）A．40° B．45° C．35° D．25°5.如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：①∠AOB＝90°+∠C；②AE+BF＝EF；③当∠C＝90°时，E，F分别是AC，BC的中点；④若OD＝a，CE+CF＝2b，则S△CEF＝ab．其中正确的是（　　）A．①② B．③④ C．①②④ D．①③④6.如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为(   )A．40° B．55° C．65° D．75°7.在△ABC和△DEF中，已知∠C=∠D，∠B=∠E，要用ASA判定这两个三角形全等，还需要条件（　　）A．BC=ED B．AB=FD C．AC=FD D．∠A=∠F8.如图，在中，平分于点给出下列结论．; ③， 平分，其中正确的有（    ）个A． B． C． D．9.如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按图中所标注的数据，计算图中实线所围成的面积S是（    ）A．50 B．62 C．65 D．6810.如图，已知点O是△ABC内一点，且点O到三边的距离相等，∠A=40゜，则∠BOC=（  ）A．130° B．140° C．110° D．120° 二、填空题11、已知：如图，OAD≌OBC，且∠O＝70°，∠C＝25°，则∠AEB＝______度．12.△ABC中，AB=5，AC=a，BC边上的中线AD=4，则a的取值范围是_____．13.现有A、B两个大型储油罐，它们相距2km，计划修建一条笔直的输油管道，使得A、B两个储油罐到输油管道所在直线的距离都为0.5km，输油管道所在直线符合上述要求的设计方案有_____种．14.如图，若D为BC中点，那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 _______．15.如图，点在上，于点，交于点，．若°，则=_________．16.任意一个三角形被一条中线分成两个三角形，则这两个三角形：①形状相同；②面积相等；③全等．上述说法中，正确的是________ ．17.如图10，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带________去配，这样做的数学依据是是_______________________________． 18.如图，已知∠MON＝80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合)，连接AC交射线OE于点D．当AB⊥OM，且△ADB有两个相等的角时，∠OAC的度数为______________． 三、解答题19、如图，点A，E，F在直线l上，AE=BF，AC//BD，且AC=BD，求证：CF=DE20.如图，点M是线段AB中点，AD、BC交于点N，连接AC、BD、MC、MD，∠l=∠2，∠3=∠4．（1）求证：△AMD≌△BMC；（2）图中在不添加新的字母的情况下，请写出除了“△AMD≌△BMC”以外的所有全等三角形，并选出其中一对进行证明．    21.如图，已知BE⊥AD，CF⊥AD，且BE=CF，请你判断AD是ΔABC的中线还是角平分线？请说明你的理由.    22.如图，A，D，E三点在同一直线上，且△BAD≌△ACE，试说明：(1)BD=DE+CE；(2)△ABD满足什么条件时,BD∥CE．     23.已知△ABN和△ACM的位置如图所示，∠1=∠2，AB=AC，AM=AN，求证：∠M=∠N.      24.如图，Rt△ABC中，AB=AC，∠BAC=90°，直线AE是经过点A的任一直线，BD⊥AE于D，CE⊥AE于E，若BD＞CE，试解答：（1）AD与CE的大小关系如何？请说明理由;（2）若BD=5,CE=2,求DE的长.   探究问题1  已知：如图1，三角形ABC中，点D是AB边的中点，AE⊥BC，BF⊥AC，垂足分别为点E，F，AE，BF交于点M，连接DE，DF．若DE=kDF，则k的值为　   　．拓展问题2  已知：如图2，三角形ABC中，CB=CA，点D是AB边的中点，点M在三角形ABC的内部，且∠MAC=∠MBC，过点M分别作ME⊥BC，MF⊥AC，垂足分别为点E，F，连接DE，DF．求证：DE=DF．推广问题3  如图3，若将上面问题2中的条件“CB=CA”变为“CB≠CA”，其他条件不变，试探究DE与DF之间的数量关系，并证明你的结论．参考答案： 一、1、C 2、C 3、B 4、B 5、C 6、C 7、A 8、B 9、A 10、C二、11、12012、3＜a＜1313、414、AB=AC15、55°16、②17、③    两角和它们的夹边分别相等的两个三角形全等18、10°、25°、40°. 三、解答题19、见解析.【分析】利用SAS证明△ACF≌△BDE，根据全等三角形的性质即可得.【详解】∵AE＝BF，∴AF＝BE，∵AC∥BD，∴∠CAF＝∠DBE，又AC＝BD，∴△ACF≌△BDE(SAS)，∴CF＝DE.【点睛】本题考查了全等三角形的判定与性质，熟练掌握是解题的关键.20、（1）详见解析；（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．【分析】（1）根据ASA即可判断；（2）全等三角形有：△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．根据三角形全等的判定方法一一判断即可.【详解】（1）∵点M是AB中点，∴AM=BM，∵∠1=∠2，∴∠AMD=∠BMC，在△AMD和△BMC中，，∴△AMD≌△MBC（ASA）；（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．理由：∵△AMD≌△MBC，∴AD=BC，∵∠3=∠4，AB=BA，∴△BAD≌△ABC（SAS），∴AC=BD，∠BDN=∠ACN，∵∠ANC=∠BND，∴△ANC≌△BND（AAS），∵AC=BD，∠CAM=∠DBM，AM=BM，∴△AMC≌△BMD（SAS）．【点睛】本题考查了全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质．21、中线，理由见试题解析．【详解】试题分析：我们可以通过证明△BDE和△CDF全等来确定其为中线．试题解析：AD是△ABC的中线．理由如下：∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD=90°，在△BDE和△CDF中，∵∠BED=∠CFD，∠BDE=∠CDF，BE=CF，∴△BDE≌△CDF（AAS），∴BD=CD．∴AD是△ABC的中线．考点：1．直角三角形全等的判定；2．全等三角形的性质．22、（1）证明见解析；（2）∠ADB=90°．【分析】（1）根据全等三角形的性质求出BD=AE，AD=CE，代入求出即可；（2）根据全等三角形的性质求出∠E=∠BDA=90°，推出∠BDE=90°，根据平行线的判定求出即可．【详解】解：(1)∵△BAD≌△ACE，∴BD=AE，AD=CE，∴BD=AE=AD+DE=CE+DE，即BD=DE+CE；(2)△ABD满足∠ADB=90°时,BD∥CE，理由是：∵△BAD≌△ACE，∴∠E=∠ADB=90°，∴∠BDE=180°−90°=90°=∠E，∴BD∥CE．【点睛】本题考查了全等三角形的性质和平行线的判定等的应用，关键是通过三角形全等得出正确的结论，通过做此题培养了学生分析问题的能力． 23、见解析【分析】证出∠BAN=∠CAM，由AB=AC，AM=AN证明△ACM≌△ABN，得出对应角相等即可．【详解】∵∠1=∠2，∴∠BAN=∠CAM ，AB=AC，AM=AN，∴△ABN≌△ACM，∴∠M=∠N.【点睛】本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．24、（1）AD=CE，理由见解析；（2）3.【详解】试题分析：（1）利用角角边证出△ABD≌△CAE；得出BD=AE，AD=CE；（2）证法同上，从而得出BD=DE+CE.试题解析：（8分）（1）AD＝CE因为∠BAC＝90°，BD⊥AE，所以∠ABD＝∠CAE， 又因为AB＝AC，∠ADB＝∠AEC＝90°，根据“AAS”可得△ABD≌△CAE， 所以AD＝CE. （2）因为△ABD≌△CAE，所以BD＝AE，所以DE＝AE－AD＝BD－CE=5－2=3.考点：全等三角形的判定.25、（1）1；（2）证明见解析；（3）DE=DF，理由见解析.【分析】（1）利用直角三角形的性质“直角三角形斜边中线等于斜边的一半”得到DE=DF；（2）利用等腰三角形的性质和判定得出结论，从而判定△MEB≌△MFA（AAS），得到DE=DF．（3）利用三角形的中位线和直角三角形的性质根据SAS证明△DHE≌△FGD可得．【详解】（1）∵AE⊥BC，BF⊥AC∴△AEB和△AFB都是直角三角形∵D是AB的中点∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线∴DE=AB，DF=AB（直角三角形斜边中线等于斜边的一半）∴DE=DF∵DE=kDF∴k=1（2）∵CB=CA∴∠CBA=∠CAB∵∠MAC=∠MB∴∠CBA﹣∠MBC=∠CAB﹣∠MAC即∠ABM=∠BAM∴AM=BM∵ME⊥BC，MF⊥AC∴∠MEB=∠MFA=90又∵∠MBE=∠MAF∴△MEB≌△MFA（AAS）∴BE=AF∵D是AB的中点，即BD=AD又∵∠DBE=∠DAF∴△DBE≌△DAF（SAS）∴DE=DF（3）DE=DF如图1，作AM的中点G，BM的中点H，∵点 D是 边 AB的 中点∴DG∥BM，DG=BM 同理可得：DH∥AM，DH=AM∵ME⊥BC于E，H 是BM的中点∴在Rt△BEM中，HE=BM=BH∴∠HBE=∠HEB∠MHE=∠HBE+∠HEB=2∠MBC又∵DG=BM，HE=BM∴DG=HE同理可得：DH=FG，∠MGF=2∠MAC∵DG∥BM，DH∥GM∴四边形DHMG是平行四边形∴∠DGM=∠DHM∵∠MGF=2∠MAC，∠MHE=2∠MBC又∵∠MBC=∠MAC∴∠MGF=∠MHE∴∠DGM+∠MGF=∠DHM+∠MHE∴∠DGF=∠DHE在△DHE与△FGD中，∴△DHE≌△FGD（SAS），∴DE=DF【点睛】本题主要考查三角形全等的判定和性质；在证明三角形全等时，用到的知识点比较多，用到直角三角形的性质、三角形的中位线、平行四边形的性质和判定．