高中数学人教A版 (2019)必修 第一册5.6 函数 y=Asin（ ωx ＋ φ）第2课时达标测试

课时作业19　分段函数

时间：45分钟

——基础巩固类——

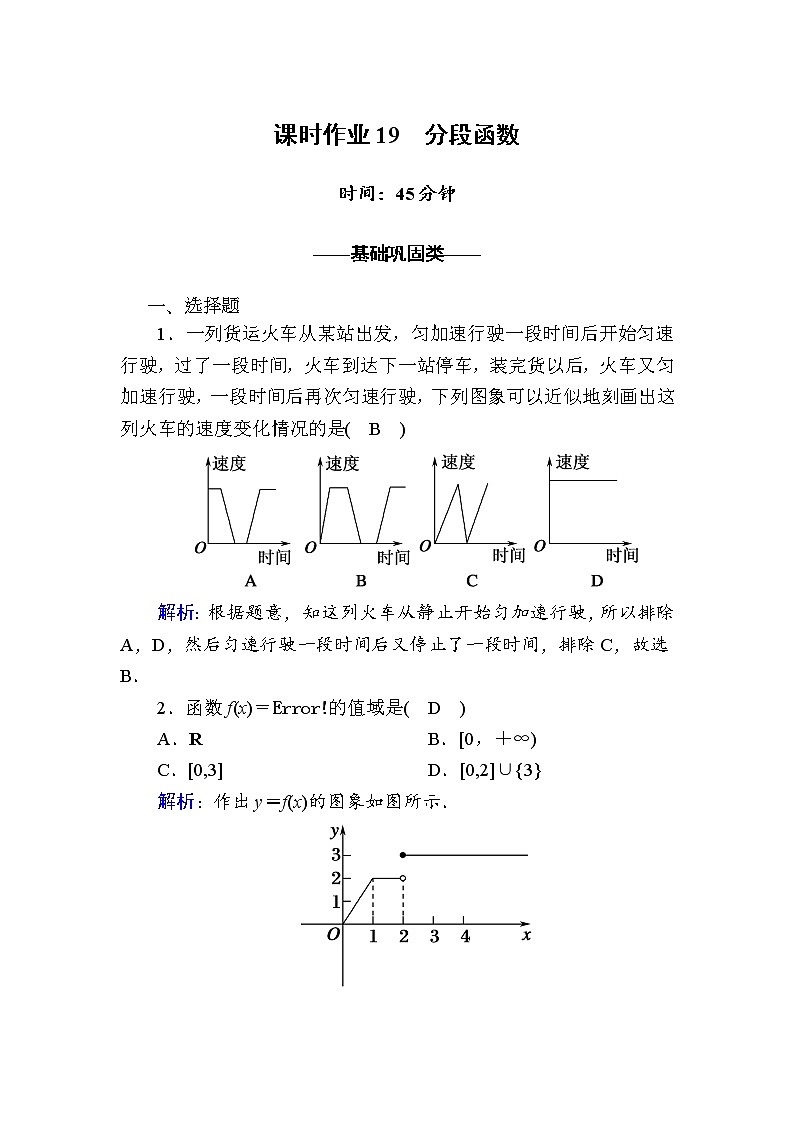
1．一列货运火车从某站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一站停车，装完货以后，火车又匀加速行驶，一段时间后再次匀速行驶，下列图象可以近似地刻画出这列火车的速度变化情况的是(　B　)

解析：根据题意，知这列火车从静止开始匀加速行驶，所以排除A，D，然后匀速行驶一段时间后又停止了一段时间，排除C，故选B．

2．函数f(x)＝的值域是(　D　)

A．R    B．[0，＋∞)

C．[0,3]    D．[0,2]∪{3}

解析：作出y＝f(x)的图象如图所示．

由图知，f(x)的值域是[0,2]∪{3}．

3．已知f(x)＝则f(3)为(　A　)

A．2　　　　　B．3　　　　　C．4　　　　　D．5

解析：f(3)＝f(3＋2)＝f(5)，f(5)＝f(5＋2)＝f(7)．

∵f(7)＝7－5＝2，故f(3)＝2.

4．已知函数f(x)＝若f(x)＝3，则x的值是(　A　)

A．    B．9

C．－1或1    D．－或

解析：依题意，若x≤0，则x＋2＝3，解得x＝1，不合题意，舍去．若0<x≤3，则x2＝3，解得x＝－(舍去)或x＝.故选A．

5．函数f(x)＝x＋的图象是(　C　)

解析：依题意，知f(x)＝x＋＝

所以函数f(x)的图象为选项C中的图象．故选C．

6．拟定从甲地到乙地通话m分钟的话费符合f(m)＝其中[m]表示不超过m的最大整数，从甲地到乙地通话5.2分钟的话费是(　C　)

A．3.71    B．4.24

C．4.77    D．7.95

解析：f(5.2)＝1.06×(0.5×[5.2]＋2)＝1.06×(2.5＋2)＝4.77.

7．若定义运算a⊙b＝则函数f(x)＝x⊙(2－x)的值域为(－∞，1]．

解析：由题意得f(x)＝

画出函数f(x)的图象(如图)得值域是(－∞，1]．

8．某商品的单价为5 000元，若一次性购买超过5件，但不超过10件时，每件优惠500元；若一次性购买超过10件，则每件优惠800元．某单位需要购买x(x∈N*，x≤15)件该商品，设购买总费用是f(x)元，则f(x)的解析式是f(x)＝.

解析：当x≤5，x∈N*时，f(x)＝5 000x；当5<x≤10，x∈N*时，f(x)＝(5 000－500)x＝4 500x；当10<x≤15，x∈N*时，f(x)＝(5 000－800)x＝4 200x.所以f(x)的解析式是f(x)＝

9．设函数f(x)＝若f(－4)＝f(0)，f(－2)＝－2，则关于x的方程f(x)＝x的解的个数是3.

解析：由f(－4)＝f(0)⇒(－4)2＋b×(－4)＋c＝c，f(－2)＝－2⇒(－2)2＋b×(－2)＋c＝－2，解得b＝4，c＝2.则f(x)＝

由f(x)＝x，得x2＋4x＋2＝x⇒x2＋3x＋2＝0⇒x＝－2或x＝－1，即当x≤0时，有两个解．当x>0时，有一个解x＝2.综上，f(x)＝x有3个解．

10．已知函数f(x)＝

(1)求f(f(f(5)))的值；

(2)画出函数的图象．

解：(1)因为5>4，所以f(5)＝－5＋2＝－3.

因为－3<0.

所以f(f(5))＝f(－3)＝－3＋4＝1.

因为0<1<4，所以f(f(f(5)))＝f(1)＝12－2×1＝－1.

即f(f(f(5)))＝－1.

(2)图象如图所示．

11．已知函数f(x)的图象如图所示，求f(x)的解析式．

解：当x≤－2时，函数f(x)的图象为一条射线，且经过点(－2，0)与点(－4,3)，

设f(x)＝ax＋b(a≠0)，将两点的坐标代入，

得解得

所以此时函数f(x)的解析式为f(x)＝－x－3(x≤－2)；

当－2<x<2时，函数f(x)的图象为一条平行于x轴的线段(不包括端点)，且经过点(0,2)，

所以此时函数f(x)的解析式为f(x)＝2(－2<x<2)；

当x≥2时，函数f(x)的图象为一条射线，且经过点(2,2)与点(3,3)，

设f(x)＝cx＋d(c≠0)，将两点的坐标代入，

得解得

所以此时函数f(x)的解析式为f(x)＝x(x≥2)．

综上，得f(x)＝

——能力提升类——

12．设函数f(x)＝若f(f())＝4，则b＝(　D　)

A．1    B．

C．    D．

解析：f(f())＝f(3×－b)＝f.

当－b<1，即b>时，3×－b＝4，

解得b＝(舍)．

当－b≥1，即b≤时，2×＝4，

解得b＝.故选D．

13．某单位为鼓励职工节约用水，作出了如下规定：每位职工每月用水量不超过10立方米的，按每立方米m元收费；用水量超过10立方米的，超过部分按每立方米2m元收费．某职工某月缴水费16m元，则该职工这个月实际用水量为(　A　)

A．13立方米    B．14立方米

C．18立方米    D．26立方米

解析：该单位职工每月应缴水费y与实际用水量x满足的关系式为y＝由y＝16m，可知x>10.令2mx－10m＝16m，解得x＝13.

14．定义在R上的函数f(x)满足f(x＋1)＝2f(x)．若当0≤x≤1时，f(x)＝x(1－x)，则当－1≤x≤0时，f(x)＝－.

解析：当－1≤x≤0时，0≤x＋1≤1，

所以f(x＋1)＝(x＋1)[1－(x＋1)]＝－x(x＋1)，

又f(x＋1)＝2f(x)，

所以f(x)＝f(x＋1)＝－.

15．如图所示，在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点(起点)向A点(终点)移动．设P点移动的路程为x，△ABP的面积为y＝f(x)．

(1)求△ABP的面积与P移动的路程的函数关系式；

(2)作出函数的图象，并根据图象求f(x)的最大值．

解：(1)函数的定义域为(0,12)．当0<x≤4时，S＝f(x)＝×4×x＝2x；当4<x≤8时，S＝f(x)＝×4×4＝8；当8<x<12时，S＝f(x)＝×4×(12－x)＝24－2x.

∴函数解析式为

f(x)＝

(2)图象如图所示．从图象可以看出[f(x)]max＝8.