数学3.1.1方程的根与函数的零点课堂教学ppt课件

这是一份数学3.1.1方程的根与函数的零点课堂教学ppt课件，共16页。PPT课件主要包含了问题一，问题二，合作探究一，函数零点的定义，对零点的理解，数的角度，形的角度，合作探究二，典例分析，例3求函数等内容，欢迎下载使用。

问题一：方程 有实数根吗？
思考：一元二次方程ax2+bx+c=0(a>0)的根与二次函数y=ax2+bx+c(a>0)的图象有什么关系？
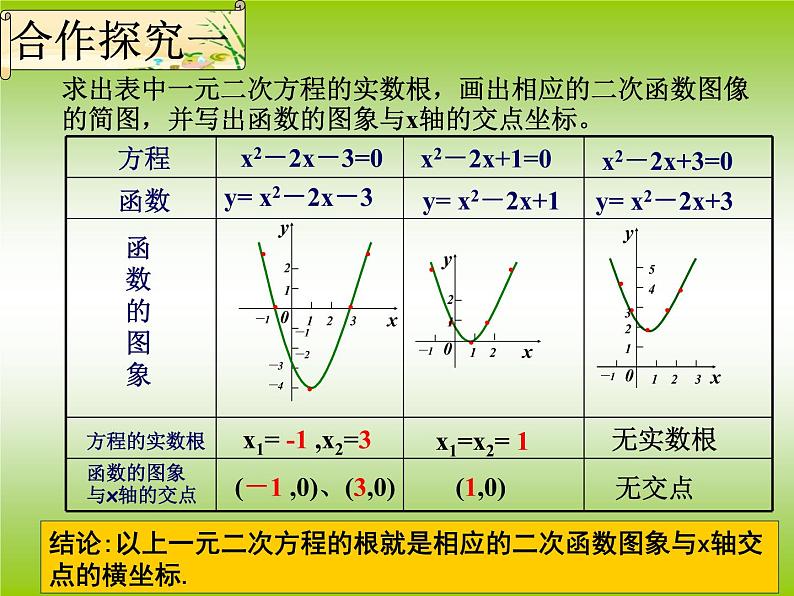
x1= -1 ,x2=3
(－1 ,0)、(3,0)
求出表中一元二次方程的实数根，画出相应的二次函数图像的简图，并写出函数的图象与x轴的交点坐标。
结论:以上一元二次方程的根就是相应的二次函数图象与x轴交点的横坐标.
函数的图象与x轴的交点
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
注意：零点指的是一个实数，而不是一个点！
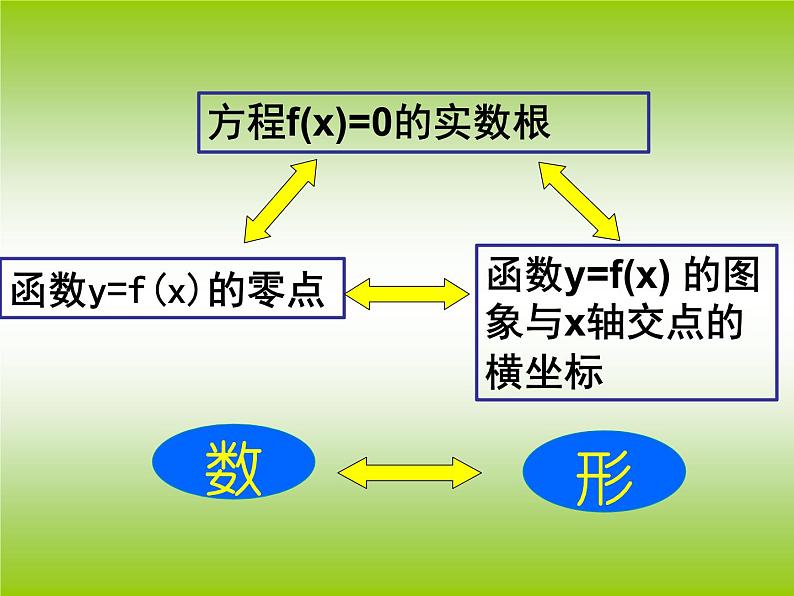
使f(x)=0的实数x的值
函数f(x)的图象与x轴的交点的横坐标
方程f(x)=0的实数根
函数y=f(x) 的图象与x轴交点的横坐标
函数y=f(x)的零点
解： (1)令y=0,即x2-x=0；
解得x1=0，x2=1
∴所求函数的零点是0和1
例1、求下列函数的零点：（注意格式）
(2) 1 (3) 0
例2：已知函数　 是定义域为Ｒ的奇函数，且　　 在　　　上有一个零点，则 的零点个数为( ) Ａ.３ Ｂ.２ Ｃ.１ Ｄ.不确定
提升：这三个零点的和是多少？
方程 是否有实根？有几个实根？
某地0--12时气温变化如图，中间一部分看不清楚，假设气温是连续变化的，请将图形补充成完整的函数图像，这段时间内，是否一定有某时刻的气温为0°C?为什么？
用求根法确定该函数另一零点的范围，并用上述方法加以验证！
你会从数来刻画这一图形特征吗？
形的直观、数的精细、互为印证、相得益彰.
思考1:若只给条件f(a) · f(b)<0,能否保证函数y=f(x)在(a,b)一定有零点？
思考2：若函数y=f(x)在区间(a,b)内有零点，则f(a)·f(b)<0一定成立吗?
（1）函数图象必须是连续的
解法一：作出x、f(x)的对应值表．
由表格可知f(2)<0,f(3)>0，即f(2)·f(3)<0，说明这个函数在区间(2,3)内有零点．
由于函数f(x)在定义域(0,+∞)内是增函数，所以它有且仅有一个零点．
例3：求函数 的零点个数.
解法二：将函数f(x)=lnx+2x-6的零点个数转化为函数g(x)=lnx与h(x)=-2x+6的图象交点的个数。
那么函数在区间[1，6]上的零点至少有（ ）个A. 2个B. 3个 C. 4个D. 5个2.函数f (x)= – x 3 – 3x + 5的零点所在的大致区间 为 （ ）A. ( – 1 ，0) B. (0，1) C. (1，2) D. (2，3)
1.已知函数f (x)的图象是连续不断的，有如下 对应值表：