
人教版新课标A必修13.1.1方程的根与函数的零点教案设计
展开
3.1.1 函数零点的存在性定理
(一)教学目标
1.知识与技能
体验零点存在性定理的形成过程,理解零点存在性定理,并能应用它探究零点的个数及存在的区间.
2.过程与方法
经历由特殊到一般的过程,在由了解零点存在性定理到理解零点存在性定理,从而掌握零点存在性定理的过程中,养成研究问题的良好的思维习惯.
3.情感、态度与价值观
经历知识发现、生成、发展、掌握、理解的过程,学会观察问题,发现问题,从而解决问题;养成良好的科学态度,享受探究数学知识的乐趣.
(二)教学重点与难点
重点:掌握零点存在性定理并能应用.
难点:零点存在性定理的理解
(三)教学方法
通过问题发现生疑,通过问题解决析疑,从而获取知识形成能力;应用引导与动手尝试结合教学法,即学生自主探究与教师启发,引导相结合.
(四)教学过程
教学环节 | 教学内容 | 师生互动 | 设计意图 | ||||||||||||||||||||||||
复习回顾提出问题 | 1.函数零点的概念 2.函数零点与方程根的关系 3.实例探究 已知函数y= x2+4x– 5,则其零点有几个?分别为多少? | 生:口答零点的定义,零点与根的关系 师:回顾零点的求法 生:函数y= x2+4x– 5的零点有2个,分别为–5,1 | 回顾旧知, 引入新知 | ||||||||||||||||||||||||
示例探究引入课题 | 1.探究函数y = x2 + 4x – 5的零点所在区间及零点存在区间的端点函数值的正负情况的关系 | 师:引导学生利用图象观察零点的所在区间,说明区间端一般取整数. 生:零点–5∈(–6,–4) 零点1∈(0,2) 且f (–6)·f (–4)<0 f (0)·f (2)<0 师:其它函数的零点是否具有相同规律呢?观察下列函数的零点及零点所在区间. ①f (x) = 2x – 1, ②f (x) = log2(x – 1) 生:函数f (x) = 2x – 1的零点为且f (0) f (1)<0. 函数f (x) = log2(x – 1)的零点为2∈(1,3)且f (1) f (3)<0 | 由特殊到一般,归纳一般结论,引入零点存在性定理 | ||||||||||||||||||||||||
发现定理 | 零点存在性定理 如果函数y = f (x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f (a)·f (b)<0那么,函数y = f (x)在区间[a,b]内有零点,即存在c∈(a,b),使得f (c) = 0这个c也就是方程f (x) = 0的根 | 师生合作分析,并剖析定理中的关键词 ①连续不断 ②f (a)·f (b)<0 师:由于图象连续不断, 若f (a)>0,f (b)<0,则y = f (x)的图象将从x轴上方变化到下方,这样必通过x轴,即与x轴有交点 | 形成定理,分析关键词,了解定理. | ||||||||||||||||||||||||
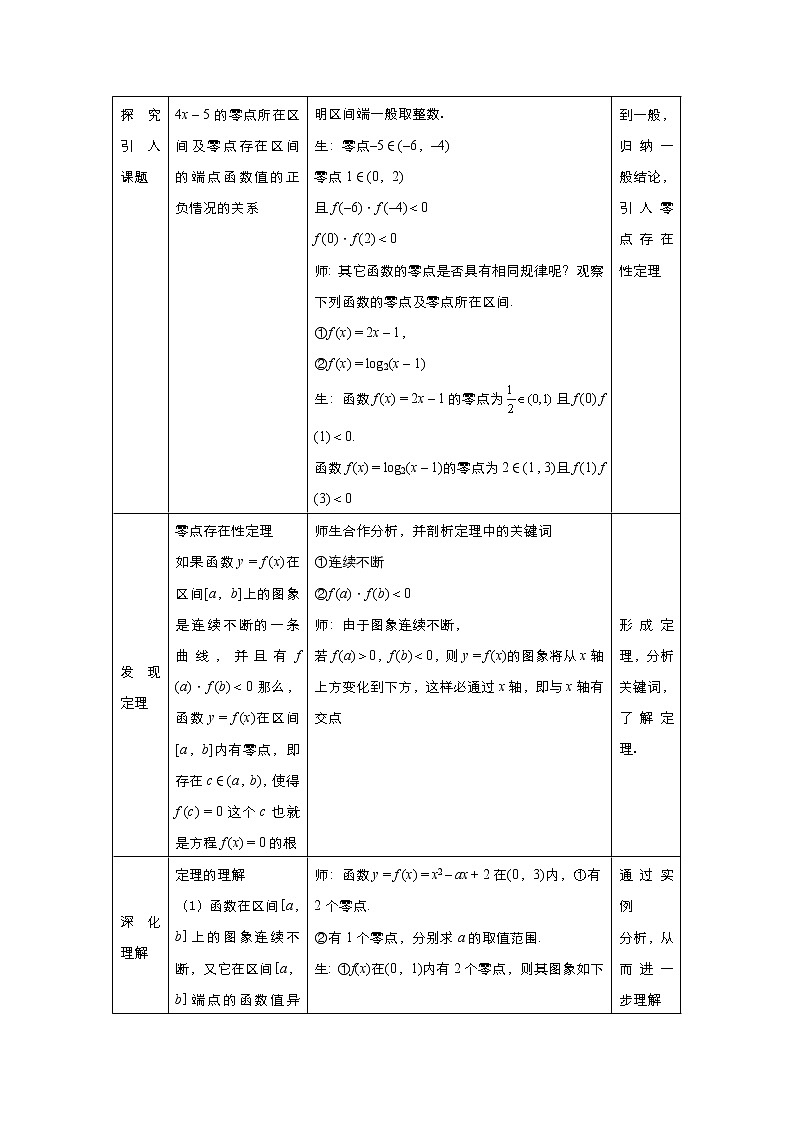
深化理解 | 定理的理解 (1)函数在区间[a,b]上的图象连续不断,又它在区间[a,b]端点的函数值异号,则函数在[a,b]上一定存在零点 (2)函数值在区间[a,b]上连续且存在零点,则它在区间[a,b]端点的函数值可能异号也可能同号 (3)定理只能判定零点的存在性,不能判断零点的个数 | 师:函数y = f (x) = x2 – ax + 2在(0,3)内,①有2个零点. ②有1个零点,分别求a的取值范围. 生:①f(x)在(0,1)内有2个零点,则其图象如下
则 ②f(x)在(0,3)内有1个零点 则 | 通过实例 分析,从而进一步理解 定理,深化 定理. | ||||||||||||||||||||||||
应用举例 |
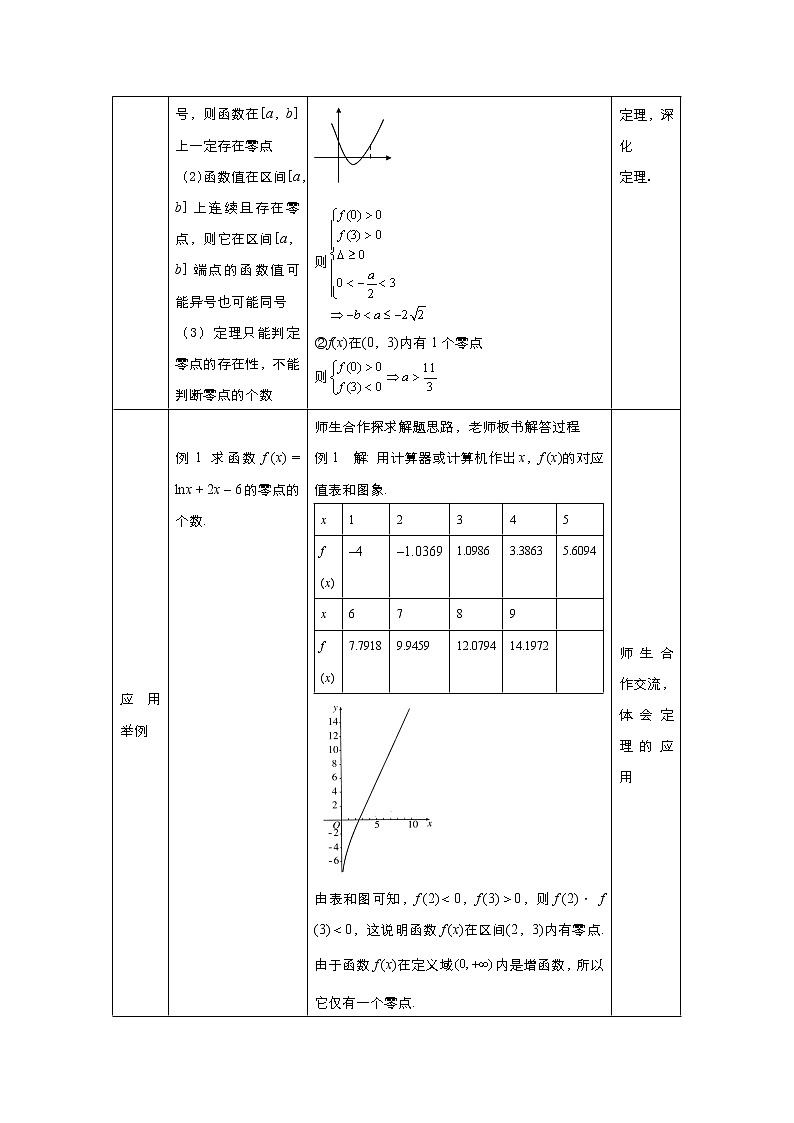
例1 求函数f (x) = lnx + 2x – 6的零点的个数. | 师生合作探求解题思路,老师板书解答过程 例1 解:用计算器或计算机作出x,f (x)的对应值表和图象.
由表和图可知,f (2)<0,f (3)>0,则f (2)· f (3)<0,这说明函数f (x)在区间(2,3)内有零点.由于函数f (x)在定义域内是增函数,所以它仅有一个零点. | 师生合作交流,体会定理的应用 | ||||||||||||||||||||||||
练习巩固 |
练习1.利用信息技术作出函数的图象,并指出下列函数零点所在的大致区间: (1)f (x) = –x3 –3x + 5; (2)f (x) = 2x·ln(x – 2) – 3; (3)f (x) =ex–1 + 4x – 4; (4)f (x) = 3 (x + 2) (x – 3) (x + 4) + x. | 学生尝试动手练习,老师借助计算机作图,师生合作交流分析,求解问题. 练习1解:(1)作出函数图象,因为f (1) = 1>0,f (1,5 ) = –2.875<0所以f (x) = –x3 –3x + 5在区间(1,1.5)上有一个零点. 又因为 f(x)是上的减函数,所以f(x) = –x3 –3x + 5在区间(1,1.5)上有且只有一个零点. (2)作出函数图象,因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x–2) –3在区间(3,4)上有一个零点. 又因为f(x)=2x·ln(x–2) –3在上是增函数,所以f(x) 在上有且仅有一个(3,4)上的零点 (3)作出函数图象,因为f(0)<0,f(1)>0,所以f (x) =ex–1 + 4x – 4在区间(0,1)上有一个零点 又因为f(x) =ex–1 + 4x – 4在上是增函数,所以f(x)在上有且仅有一个零点. (4)作出函数图象,因为f (–4)<0,f (–3)>0,f (–2)<0,f (2)<0,f (3)>0,所以f (x) = 3 (x + 2) (x – 3) (x + 4) + x在(–4,–3),(–3, –2),(2,3)上各有一个零点 . | 尝试学生动手模仿练习,老师引导、启发,师生合作完成问题求解,从而固化知识与方法,提升思维能力. | ||||||||||||||||||||||||
归纳总结 | 1.数形结合探究函数零点 2.应用定理探究零点及存在区间. 3.定理应用的题型:判定零点的存在性及存在区间. | 学生总结师生完善补充 | 学会整理知识,培养自我归纳知识的能力 | ||||||||||||||||||||||||
课后练习 | 3.1第二课时 习案 | 学生自主完成 | 整合知识,提升能力 |
备选例题
例1 已知集合A = {x∈R|x2 – 4ax + 2a + 6 = 0},B = { x∈R|x<0},若A∩B≠,求实数a的取值范围.
【解析】设全集U = {a|△= (–4a)2 – 4 (2a + 6)≥0}
=
=
若方程x2 – 4ax + 2a + 6 = 0的两根x1,x2均非负,则
因为在全集U中集合的补集为{a|a≤–1},所以实数a的取值范围是{a|a≤–1}.
例2 设集合A = {x | x2 + 4x = 0,x∈R},B = {x | x2 + 2 (a + 1) x + a2 – 1 = 0, x∈R},若A∪B = A,求实数a的值.
【解析】∵A = {x | x2 + 4x = 0,x∈R},∴A = {–4,0}.
∵A∪B=A,∴BA.
1°当B = A,即B = {–4,0}时,由一元二次方程根与系数的关系得
2°当B=,即方程x2 + 2 (a + 1)x + a2 –1 = 0无实解.
∴△= 4 (a + 1)2 – 4 (a2 – 1) = 8a + 8<0.
解得,a<–1.
3°当B = {0},即方程x2 + 2(a + 1)x + a2 – 1 = 0有两个相等的实数根且为零时,
4°当B = {–4}时,即需
无解.
综上所述,若A∪B=A,则a≤–1或a = 1.
人教版新课标A必修13.1.1方程的根与函数的零点教案: 这是一份人教版新课标A必修13.1.1方程的根与函数的零点教案,共8页。教案主要包含了温馨寄语,学习目标,学习重点,学习难点,自主学习,预习评价,合作探究,教师点拨等内容,欢迎下载使用。
高中人教版新课标A3.1.1方程的根与函数的零点教案: 这是一份高中人教版新课标A3.1.1方程的根与函数的零点教案,共5页。
人教版新课标A必修13.1.1方程的根与函数的零点教学设计: 这是一份人教版新课标A必修13.1.1方程的根与函数的零点教学设计,共10页。教案主要包含了教学目标设置,学生学情分析,教学策略分析,教学过程,板书设计教学活动等内容,欢迎下载使用。













