必修 第一册5.4 三角函数的图象与性质第2课时学案及答案

这是一份必修 第一册5.4 三角函数的图象与性质第2课时学案及答案，共9页。

过山车是一项富有刺激性的娱乐工具，该运动包含了许多物理学原理，人们在设计过山车时巧妙地运用了这些原理．如果能亲身体验一下过山车那感觉真是妙不可言．一个基本的过山车构造中，包含了爬升、滑落、倒转(儿童过山车没有倒转)，几个循环路径．
问题：(1)函数y＝sin x与y＝cs x也像过山车一样“爬升”，“滑落”，这是y＝sin x，y＝cs x的哪些性质？
(2)过山车爬升到最高点，然后滑落到最低点，然后再爬升，对应y＝sin x，y＝cs x的哪些性质？y＝sin x，y＝cs x在什么位置取得最大(小)值？
知识点 正弦函数、余弦函数的图象和性质
1.函数y＝sin x的单调递增区间唯一吗？
[提示] 不唯一．
2.函数y＝sin x取得最大值时对应的x的值唯一吗？
[提示] 不唯一．
1.思考辨析(正确的画“√”，错误的画“×”)
(1)正弦函数、余弦函数在R上都是单调函数. ( )
(2)存在x∈R满足cs x＝1.2.( )
(3)函数y＝－eq \f(1,2)sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))的最大值为0.( )
[答案] (1)× (2)× (3)√
2.(多选)在下列区间中，函数y＝sin x是单调递增的是( )
A．[0，π]B．eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π))
C．eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))D．eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,2)，2π))
[答案] CD
3.函数y＝－2cs x的最大值为________，此时x＝________.
2 π＋2kπ，k∈Z [当x＝π＋2kπ，k∈Z时y＝－2cs x取得最大值2.]
类型1 求正弦函数、余弦函数的单调区间
【例1】 求函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调区间．
[解] 令z＝x－eq \f(π,3)，则y＝2sin z.
∵z＝x－eq \f(π,3)是增函数，
∴y＝2sin z单调递增时，
函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))也单调递增．
由z∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)，
得x－eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)，
即x∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))(k∈Z)，
故函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))(k∈Z)．
同理可求函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(5π,6)，2kπ＋\f(11π,6)))(k∈Z)．
1．求函数f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))，x∈[0,2π]的单调区间．
[解] 由例题知f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))k∈Z.
又∵x∈[0,2π]，
∴0≤x≤eq \f(5π,6)或eq \f(11π,6)≤x≤2π，
同理函数f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))，x∈[0,2π]的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，\f(11π,6))).
∴函数f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))，x∈[0,2π]的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(5π,6)))，eq \b\lc\[\rc\](\a\vs4\al\c1(\f(11π,6)，2π))，单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，\f(11π,6))).
2．求函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))的单调递增区间．
[解] y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))＝－sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))，令z＝x－eq \f(π,3)，而y＝－sin z的单调递增区间是eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)＋2kπ，\f(3π,2)＋2kπ))，k∈Z，
∴令eq \f(π,2)＋2kπ≤x－eq \f(π,3)≤eq \f(3π,2)＋2kπ，k∈Z，
得eq \f(5π,6)＋2kπ≤x≤eq \f(11π,6)＋2kπ，k∈Z，
∴函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)＋2kπ，\f(11π,6)＋2kπ))，k∈Z.
1．求形如y＝Asin(ωx＋φ)＋b或形如y＝Acs(ωx＋φ)＋b(其中A≠0，ω>0，b为常数)的函数的单调区间，可以借助于正弦函数、余弦函数的单调区间，通过解不等式求得．
2．具体求解时注意两点：①要把ωx＋φ看作一个整体，若ω<0，先用诱导公式将式子变形，将x的系数化为正；②在A>0，ω>0时，将“ωx＋φ”代入正弦(或余弦)函数的单调区间，可以解得与之单调性一致的单调区间；当A<0，ω>0时同样方法可以求得与正弦(余弦)函数单调性相反的单调区间．
提醒：复合函数的单调性遵循“同增异减”的规律．
eq \a\vs4\al([跟进训练])
1．(1)函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,3)))的单调递减区间为________．
(2)已知函数y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－2x))，则它的单调递减区间为________．
(1)eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，－\f(2π,9)))，eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,9)，\f(π,3))) (2)eq \b\lc\[\rc\](\a\vs4\al\c1(kπ＋\f(π,6)，kπ＋\f(2π,3)))(k∈Z) [(1)由eq \f(π,2)＋2kπ≤3x＋eq \f(π,6)≤eq \f(3π,2)＋2kπ(k∈Z)，
得eq \f(π,9)＋eq \f(2kπ,3)≤x≤eq \f(4π,9)＋eq \f(2kπ,3)(k∈Z)．
又x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,3)))，
所以函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))，
x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,3)))的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，－\f(2π,9)))，eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,9)，\f(π,3))).
(2)y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－2x))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))，
由2kπ≤2x－eq \f(π,3)≤2kπ＋π，k∈Z，
得kπ＋eq \f(π,6)≤x≤kπ＋eq \f(2π,3)，k∈Z，∴函数y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－2x))的单调递减区间是eq \b\lc\[\rc\](\a\vs4\al\c1(kπ＋\f(π,6)，kπ＋\f(2π,3)))(k∈Z)．]
类型2 利用三角函数的单调性比较大小
【例2】 (对接教材P206例题)利用三角函数的单调性，比较下列各组数的大小．
(1)sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,18)))与sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,10)))；
(2)sin 196°与cs 156°；
(3)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))与cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(17,4)π)).
[解] (1)∵－eq \f(π,2)＜－eq \f(π,10)＜－eq \f(π,18)＜eq \f(π,2)，
∴sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,18)))＞sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,10))).
(2)sin 196°＝sin(180°＋16°)＝－sin 16°，
cs 156°＝cs(180°－24°)＝－cs 24°＝－sin 66°，
∵0°＜16°＜66°＜90°，
∴sin 16°＜sin 66°，
从而－sin 16°＞－sin 66°，
即sin 196°＞cs 156°.
(3)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))＝cseq \f(23,5)π
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(4π＋\f(3,5)π))＝cseq \f(3,5)π，
cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(17,4)π))＝cseq \f(17,4)π
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(4π＋\f(π,4)))＝cseq \f(π,4).
∵0＜eq \f(π,4)＜eq \f(3,5)π＜π，且y＝cs x在[0，π]上是单调递减的，
∴cseq \f(3,5)π＜cseq \f(π,4)，
即cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))＜cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(17,4)π)).
三角函数值大小比较的策略
(1)利用诱导公式，对于正弦函数来说，一般将两个角转化到eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))或eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，\f(3π,2)))内；对于余弦函数来说，一般将两个角转化到[－π，0]或[0，π]内．
(2)不同名的函数化为同名的函数．
(3)自变量不在同一单调区间化至同一单调区间内，借助正弦、余弦函数的单调性来比较大小．
eq \a\vs4\al([跟进训练])
2．(1)已知α，β为锐角三角形的两个内角，则以下结论正确的是( )
A．sin α＜sin β B．cs α＜sin β
C．cs α＜cs βD．cs α ＞cs β
(2)比较下列各组数的大小：
①cseq \f(15π,8)，cseq \f(14π,9)；②cs 1，sin 1.
(1)B [α，β为锐角三角形的两个内角，α＋β＞eq \f(π,2)，α＞eq \f(π,2)－β，α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，eq \f(π,2)－β∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，
所以cs α＜cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－β))＝sin β.]
(2)[解] ①cseq \f(15π,8)＝cseq \f(π,8)，cseq \f(14π,9)＝cseq \f(4π,9)，因为0＜eq \f(π,8)＜eq \f(4π,9)＜π，而y＝cs x在[0，π]上单调递减，
所以cseq \f(π,8)＞cseq \f(4π,9)，即cseq \f(15π,8)＞cseq \f(14π,9).
②因为cs 1＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－1))，而0＜eq \f(π,2)－1＜1＜eq \f(π,2)且y＝sin x在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上单调递增，所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－1))＜sin 1，
即cs 1＜sin 1.
类型3 正弦函数、余弦函数的最值问题
【例3】 (1)求函数y＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,6)，\f(π,6)))的值域；
(2)(对接教材P205例题)求函数y＝cs2x＋4sin x的最值及取到最大值和最小值时的x的集合．
(1)常借助三角函数的哪些性质求形如y＝asin x，x∈[m，n]的最值？(2)对于形如y＝asin2x＋bsin x＋c的函数如何探求其最值？
[解] (1)∵－eq \f(π,6)∴0<2x＋eq \f(π,3)∴－eq \f(1,2)∴函数y＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,6)，\f(π,6)))的值域为(－1,2)．
(2)y＝cs2x＋4sin x
＝1－sin2x＋4sin x
＝－sin2x＋4sin x＋1
＝－(sin x－2)2＋5.
所以当sin x＝1，即x＝2kπ＋eq \f(π,2)，k∈Z时，ymax＝4；
当sin x＝－1，即x＝2kπ－eq \f(π,2)，k∈Z时，ymin＝－4.
所以ymax＝4，此时x的取值集合是eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x＝2kπ＋\f(π,2)，k∈Z))))；
ymin＝－4，此时x的取值集合是eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x＝2kπ－\f(π,2)，k∈Z)))).
三角函数最值问题的3种常见类型及求解方法
(1)形如y＝asin x(或y＝acs x)型，可利用正弦函数，余弦函数的有界性，注意对a正负的讨论．
(2)形如y＝Asin(ωx＋φ)＋b(或y＝Acs(ωx＋φ)＋b)型，可先由定义域求得ωx＋φ的范围，然后求得sin(ωx＋φ)(或cs(ωx＋φ))的范围，最后求得最值．
(3)形如y＝asin2x＋bsin x＋c(a≠0)型，可利用换元思想，设t＝sin_x，转化为二次函数y＝at2＋bt＋c求最值，t的范围需要根据定义域来确定．
eq \a\vs4\al([跟进训练])
3．求函数y＝cs2x－sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,4)，\f(π,4)))的最值．
[解] y＝cs2x－sin x＝1－sin2x－sin x＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(sin x＋\f(1,2)))2＋eq \f(5,4).
因为－eq \f(π,4)≤x≤eq \f(π,4)，－eq \f(\r(2),2)≤sin x≤eq \f(\r(2),2)，
所以当sin x＝－eq \f(1,2)，即x＝－eq \f(π,6)时，函数取得最大值，ymax＝eq \f(5,4)；
当sin x＝eq \f(\r(2),2)，即x＝eq \f(π,4)时，函数取得最小值，ymin＝eq \f(1,2)－eq \f(\r(2),2).
1．函数y＝－cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上是( )
A．增函数B．减函数
C．先减后增函数D．先增后减函数
C [因为y＝cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上先增后减，所以y＝－cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上先减后增．]
2．函数f(x)＝2sin x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(3π,4)))上的最大值为( )
A．0B．－eq \r(2)
C．eq \r(2)D．2
D [∵x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(3π,4)))，∴0≤sin x≤1，
∴f(x)＝2sin x∈[0,2]．故选D.]
3．(多选)正弦函数y＝sin x，x∈R的图象的一条对称轴是( )
A．y轴B．直线x＝－eq \f(π,2)
C．直线x＝eq \f(π,2)D．直线x＝π
BC [y＝sin x的对称轴方程为x＝eq \f(π,2)＋kπ，k∈Z，故选BC.]
4．sineq \f(2π,7)________sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(15π,8)))(填“＞”或“＜”)．
＞ [sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(15π,8)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(－2π＋\f(π,8)))＝sineq \f(π,8)，
因为0＜eq \f(π,8)＜eq \f(2π,7)＜eq \f(π,2)，y＝sin x在eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))上是单调递增函数，所以sineq \f(π,8)＜sineq \f(2π,7)，即sineq \f(2π,7)＞sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(15π,8))).]
5．函数y＝1－sin 2x的单调递增区间为________．
eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)＋kπ，\f(3π,4)＋kπ))(k∈Z) [求函数y＝1－sin 2x的单调递增区间，转化为求函数y＝sin 2x的单调递减区间，
由eq \f(π,2)＋2kπ≤2x≤eq \f(3π,2)＋2kπ，k∈Z，
得eq \f(π,4)＋kπ≤x≤eq \f(3π,4)＋kπ，k∈Z，即函数的单调递增区间是eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)＋kπ，\f(3π,4)＋kπ))(k∈Z)．
回顾本节知识，自我完成以下问题：
1．如何求y＝Asin(ωx＋φ)(A>0，ω>0)的单调区间？
[提示] 把ωx＋φ看成一个整体，由2kπ－eq \f(π,2)≤ωx＋φ≤2kπ＋eq \f(π,2)(k∈Z)解出x的范围，所得区间即为单调递增区间，由2kπ＋eq \f(π,2)≤ωx＋φ≤2kπ＋eq \f(3π,2)(k∈Z)解出x的范围，所得区间即为单调递减区间．若ω＜0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．
2．如何利用函数单调性比较sin α与sin β的大小关系？
[提示] 比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断．
3．求三角函数最值或值域的常用方法有哪些？
[提示] 单调性法或配方法或换元法等．
学 习 任 务
核 心 素 养
1．掌握y＝sin x，y＝cs x的最大值与最小值，并会求简单三角函数的值域和最值．(重点、难点)
2．掌握y＝sin x，y＝cs x的单调性，并能利用单调性比较大小．(重点)
3．会求函数y＝Asin(ωx＋φ)及y＝Acs(ωx＋φ)的单调区间．(重点、易混点)
1．通过单调性与最值的计算，提升数学运算素养．
2．结合函数图象，培养直观想象素养.
解析式
y＝sin x
y＝cs x
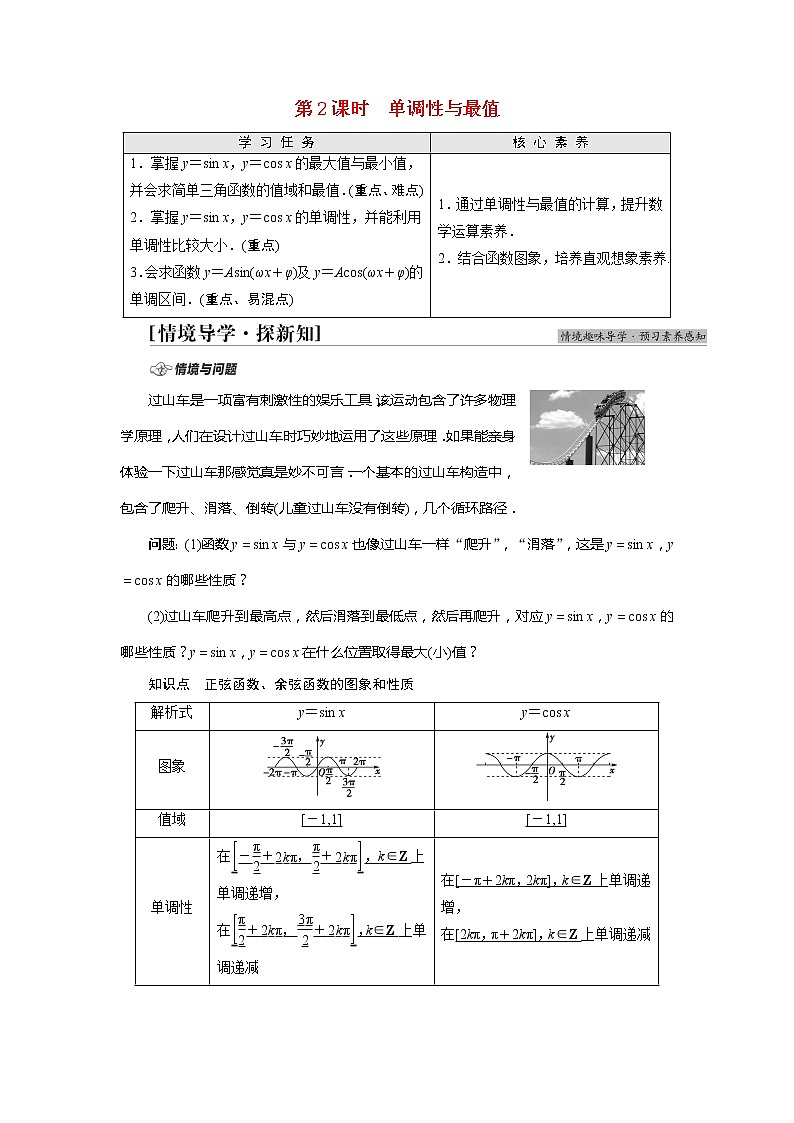
图象
值域
[－1,1]
[－1,1]
单调性
在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)＋2kπ，\f(π,2)＋2kπ))，k∈Z上单调递增，
在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)＋2kπ，\f(3π,2)＋2kπ))，k∈Z上单调递减
在[－π＋2kπ，2kπ]，k∈Z上单调递增，
在[2kπ，π＋2kπ]，k∈Z上单调递减
最值
x＝eq \f(π,2)＋2kπ，k∈Z时，ymax＝1；x＝－eq \f(π,2)＋2kπ，k∈Z时，ymin＝－1
x＝2kπ，k∈Z时，ymax＝1；x＝π＋2kπ，k∈Z时，ymin＝－1