


数学八年级上册3.1 勾股定理多媒体教学ppt课件
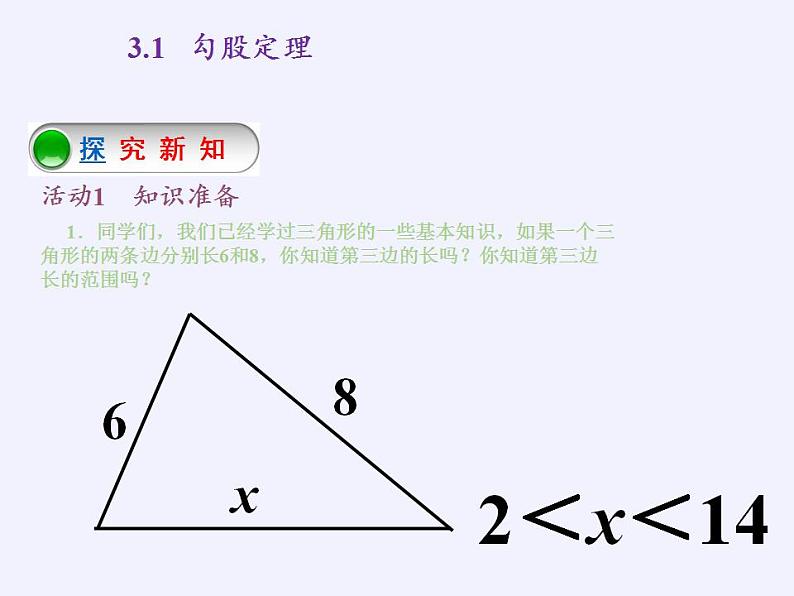
展开1.同学们,我们已经学过三角形的一些基本知识,如果一个三角形的两条边分别长6和8,你知道第三边的长吗?你知道第三边长的范围吗?
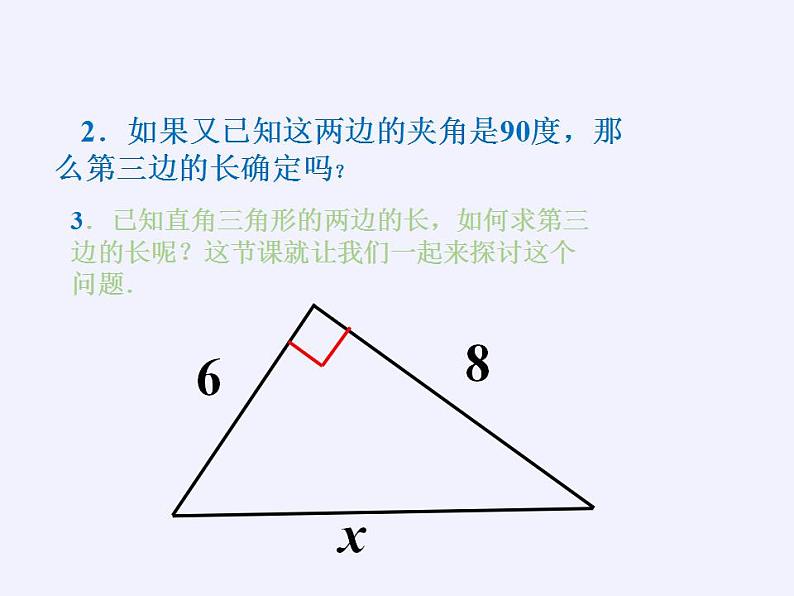
3.已知直角三角形的两边的长,如何求第三边的长呢?这节课就让我们一起来探讨这个问题.
2.如果又已知这两边的夹角是90度,那么第三边的长确定吗?
1955年希腊发行了一张邮票,图案是由三个棋盘排列而成。这张邮票是纪念二千五百年前希腊的一个学派和宗教团体 ── 毕达哥拉斯学派,它的成立以及在文化上的贡献。 邮票上的图案是根据一个著名的数学定理设计的。
(1)观察邮票图案,我们一起来数一数图案中各正方形内小方格的个数:左上方的正方形内小方格的个数为16,右上方的正方形内小方格的个数为9,最下面正方形内小方格的个数为25,发现16+9=25,猜想它们之间的关系是___________________________________________________;
两个小正方形小方格的个数之和等于大正方形小方格的个数
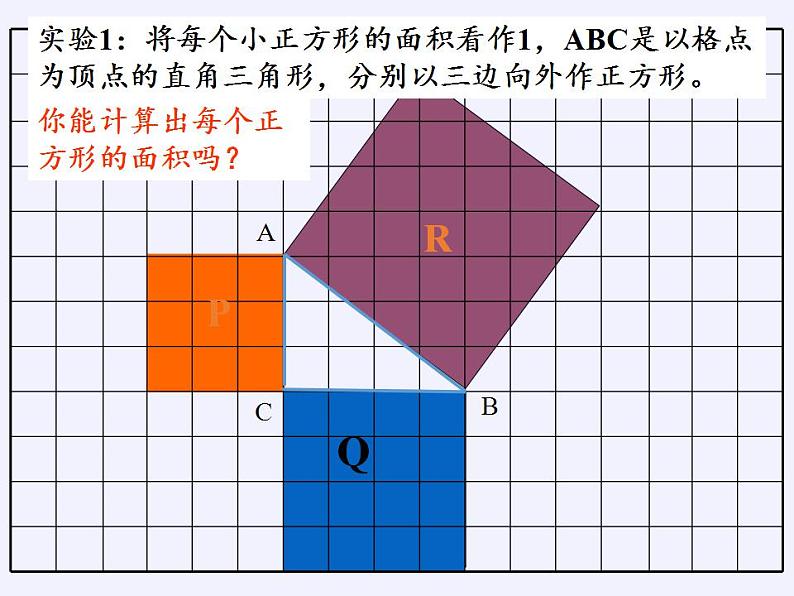
你能计算出每个正方形的面积吗?
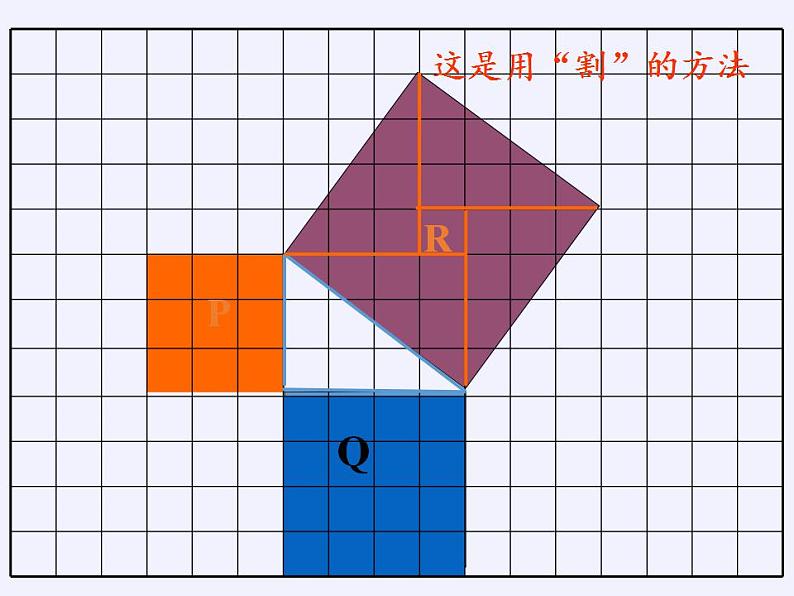
实验1:将每个小正方形的面积看作1,ABC是以格点为顶点的直角三角形,分别以三边向外作正方形。
将实验得到的数据填入表格
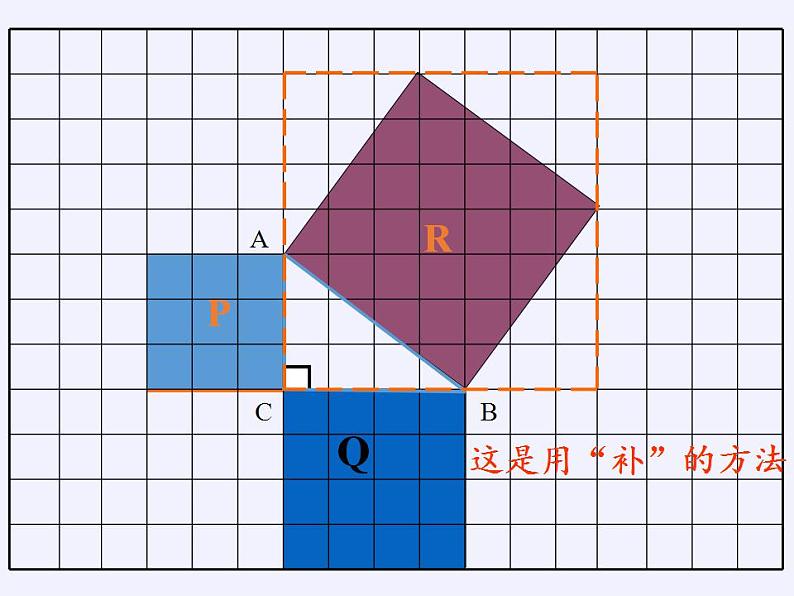
(2)计算的三个格点正方形的面积,它们之间的数量关系是________________________________.
两个小正方形的面积之和等于大正方形的面积
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
谁能用语言叙述这一结论?
观察所得到的各组数据,我们发现:
两直角边a、b与斜边c 之间的关系?
探究问题一 利用勾股定理求单个正方形的面积或直角三 角形的边长
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.(1)若c=15,b=12,求a;(2)若a=6,b=8,求c;(3)若a∶b=3∶4,c=10,求a,b.
[归纳总结] 在直角三角形中,已知两边,利用勾股定理可以求出第三边;若已知一边及另两边的关系,一般利用勾股定理列方程(思想)来求出其余两边长.
求下列直角三角形中未知边的长:
试一试,相信自己没错的!
探究问题二 综合利用勾股定理求多个直角三角形的相关边长
[解析] 在Rt△ABC中,运用勾股定理求出BC的长,再在Rt△BCD中运用勾股定理求出CD的长.
1.在Rt△ABC中,∠C=900。
(1)如果BC=3,AC=4,那么AB= ;
(2)如果BC=6,AC=8,那么AB边上的高长 为 ;
2.如图:一块长约80 m、宽约60 m的长方形草坪,被几个不自觉的学生沿对角线踏出了一条斜“路”,这种情况在生活中时有发生.请问同学们:(1)这几位同学为什么不走正路,走斜“路”?(2)走斜“路”比正路少走几步呢? (3)他们这样做,值得吗?
布置作业:1、交送作业82页第1、2两题。2、课外作业习题补充对应练习。
初中数学苏科版八年级上册3.1 勾股定理课文课件ppt: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c17054_t3/?tag_id=26" target="_blank">3.1 勾股定理课文课件ppt</a>,共18页。PPT课件主要包含了弯曲成直角的手臂,数学语言,勾股定理的由来,课堂练习,S5+S6,美丽的勾股树,勾股定理,课堂小结等内容,欢迎下载使用。
初中数学苏科版八年级上册3.1 勾股定理课文内容课件ppt: 这是一份初中数学苏科版八年级上册3.1 勾股定理课文内容课件ppt,共16页。PPT课件主要包含了1勾股定理,学习目标,导预疑学,变一变,导问研学,导法慧学等内容,欢迎下载使用。
初中数学3.1 勾股定理课前预习ppt课件: 这是一份初中数学3.1 勾股定理课前预习ppt课件,共19页。PPT课件主要包含了情境问题,a2+b2c2,勾股定理,试一试你能行等内容,欢迎下载使用。













