苏科版八年级上册第三章 勾股定理3.1 勾股定理优秀达标测试

2021年苏科版数学八年级上册

3.1《勾股定理》同步练习卷

一、选择题

1.若直角三角形的三边长分别为2，4，x，则x的值可能有(    )．

A.1个    B.2个          C.3个      D.4个

2.如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（　　）

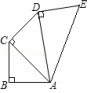
A.1         B.          C.            D.2  

3.等腰三角形的腰长为10，底长为12，则其底边上的高为（　　）

A．13           B．8           C．25              D．64

4.如图，线段AB=、CD=，那么，线段EF的长度为（　　）

A．      B．      C．      D．

5.一只蚂蚁沿直角三角形的边长爬行一周需2秒，如果将直角三角形的边长扩大1倍，那么这只蚂蚁再沿边长爬行一周需（   ）.

A.6秒        B.5秒        C.4秒        D.3秒

6.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是 (　　)

A.2         B.4           C.5           D.7

7.在Rt△ABC中，∠C=90°，若AC+BC=14cm，AB=10cm，则Rt△ABC的面积是(　　)

A.24cm2      B.36cm2      C.48cm2      D.60cm2

8.如图，在高为3米，斜坡长为5米的楼梯台阶上铺地毯，则地毯的长度至少要（　　）

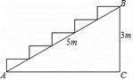
A.4米    B.5米    C.6米    D.7米

9.如图，直角△ABC的周长为24，且AB:AC=5:3，则BC=（    ）

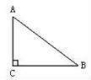
A.6    B.8              C.10   D.12

10.已知Rt△ABC中，∠A，∠B，∠C的对边分别为a,b,c，若∠B=900，则（    ）

A.b2= a2+ c2 ；   B.c2= a2+ b2；   C.a2+b2=c2；   D.a+b=c

二、填空题

11.直角三角形的两边长为5和7，则第三边长为　　.

12.一个直角三角形的两直角边为8，15，则斜边上的高为_______

13.一个正方形的面积是5，那么这个正方形的对角线的长度为　      ．

14.以直角三角形一边向外作正方形，其中两个正方形的面积为100和64，则第三个正方形的面积为　　 ．

15.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为9cm，则正方形A，B，C，D的面积之和为　　      cm2． 

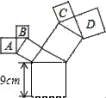
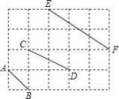
16.如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于　　.

三、作图题

17.正方形网格中，每个小正方形的边长为1.

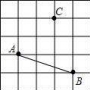
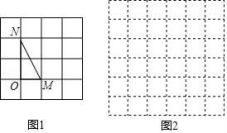
（1）如图1，格点△ONM（即△ONM三个顶点都在小正方形的顶点处），则MN=　   　.

（2）请在图2正方形网格中画出格点△ABC，且AB、BC、AC三边的长分别为、、；并求出这个三角形的面积.

四、解答题

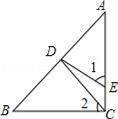
18.如图，在Rt△ABC中，∠ACB=90°，CD是AB边上的中线，DE⊥AB于点D，交AC于点E．

（1）若BC=3，AC=4，求CD的长；

（2）求证：∠1=∠2．

19.如图，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，

（1）求证：△ACE≌△BCD；

（2）若DE=13，BD=12，求线段AB的长．

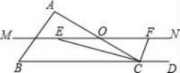
20.如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F．

（1）求证：EO=FO；（2）若CE=4,CF=3,你还能得到那些结论？

参考答案

1.B．

2.D

3.B．

4.C．

5.C

6.A

7.A

8.D

9.B

10.A

11.答案为：2或

12.答案为：

13.答案为：          

14.答案为：36或164．

15.答案为：81　

16.答案为：.

17.解：（1）MN==.故答案为.

（2）△ABC如图所示：

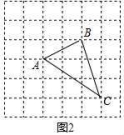
S△ABC=3×3﹣×1×2﹣×1×3﹣×2×3=.

18.（1）解：∵∠ACB=90°，BC=3，AC=4，∴AB==5，

∵CD是AB边上的中线，∴CD=AB=2.5；

（2）证明：∵∠ACB=90°，∴∠A+∠B=90°，

∵DE⊥AB，∴∠A+∠1=90°，∴∠B=∠1，

∵CD是AB边上的中线，

∴BD=CD，∴∠B=∠2，

∴∠1=∠2．

19.（1）证明：∵△ACB与△ECD都是等腰直角三角形，

∴CE=CD，AC=BC，∠ACB=∠ECD=90°，∠B=∠BAC=45°，

∴∠ACE=∠BCD=90°﹣∠ACD，

在△ACE和△BCD中

∴△ACE≌△BCD；

（2）解：∵△ACE≌△BCD，∴AE=BD，∠EAC=∠B=45°，

∵BD=12，∴∠EAD=45°+45°=90°，AE=12，

在Rt△EAD中，∠EAD=90°，DE=13，AE=12，由勾股定理得：AD=5，

∴AB=BD+AD=12+5=17．

20.解：（1）∵CE是∠ACB的平分线，∴∠1=∠2，

∵MN∥BC，∴∠1=∠3，∴∠2=∠3，∴OE=OC，同理可得OF=OC，∴OE=OF；

（2）∵CE是∠ACB的平分线，∴∠1=∠2，

∵CF是∠OCD的平分线，∴∠4=∠5，∴∠ECF=90°，

在Rt△ECF中，

由勾股定理得EF=．∴OE=OF=OC=0.5EF=2.5．