高中数学人教A版 (2019)必修 第二册8.1 基本立体图形第1课时课堂检测

这是一份高中数学人教A版 (2019)必修 第二册8.1 基本立体图形第1课时课堂检测，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
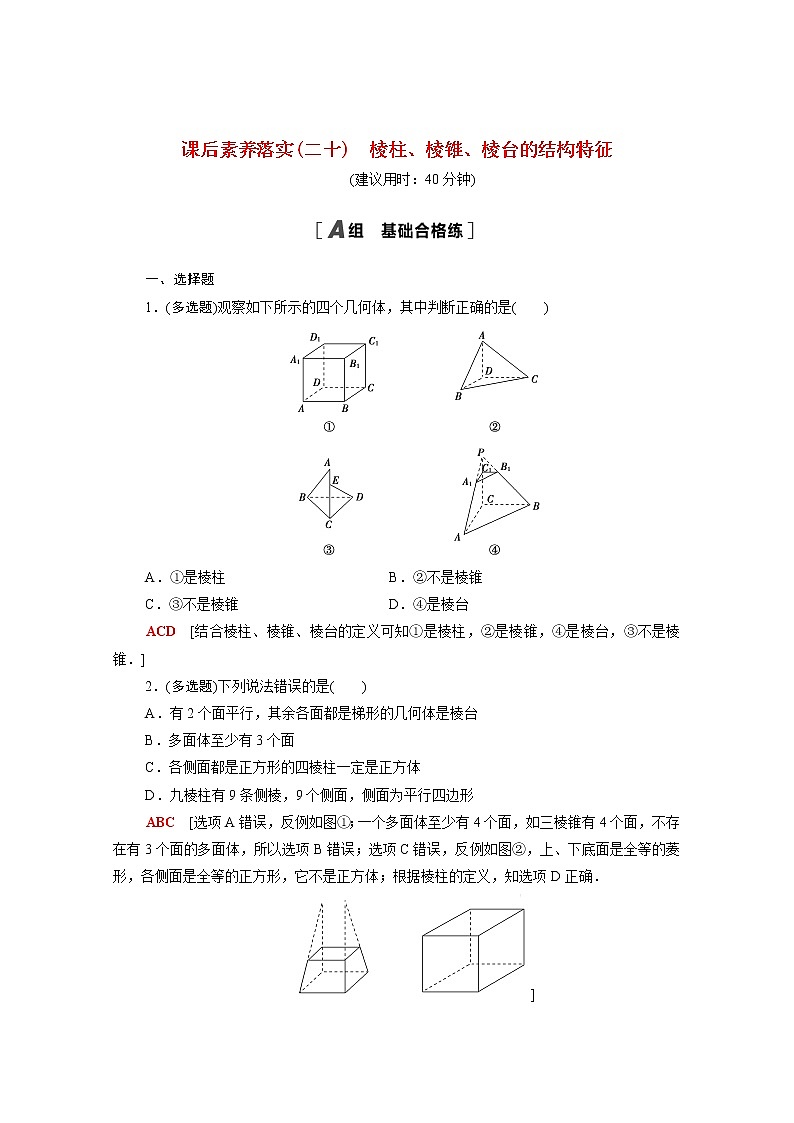
1．(多选题)观察如下所示的四个几何体，其中判断正确的是( )
A．①是棱柱 B．②不是棱锥
C．③不是棱锥 D．④是棱台
ACD [结合棱柱、棱锥、棱台的定义可知①是棱柱，②是棱锥，④是棱台，③不是棱锥．]
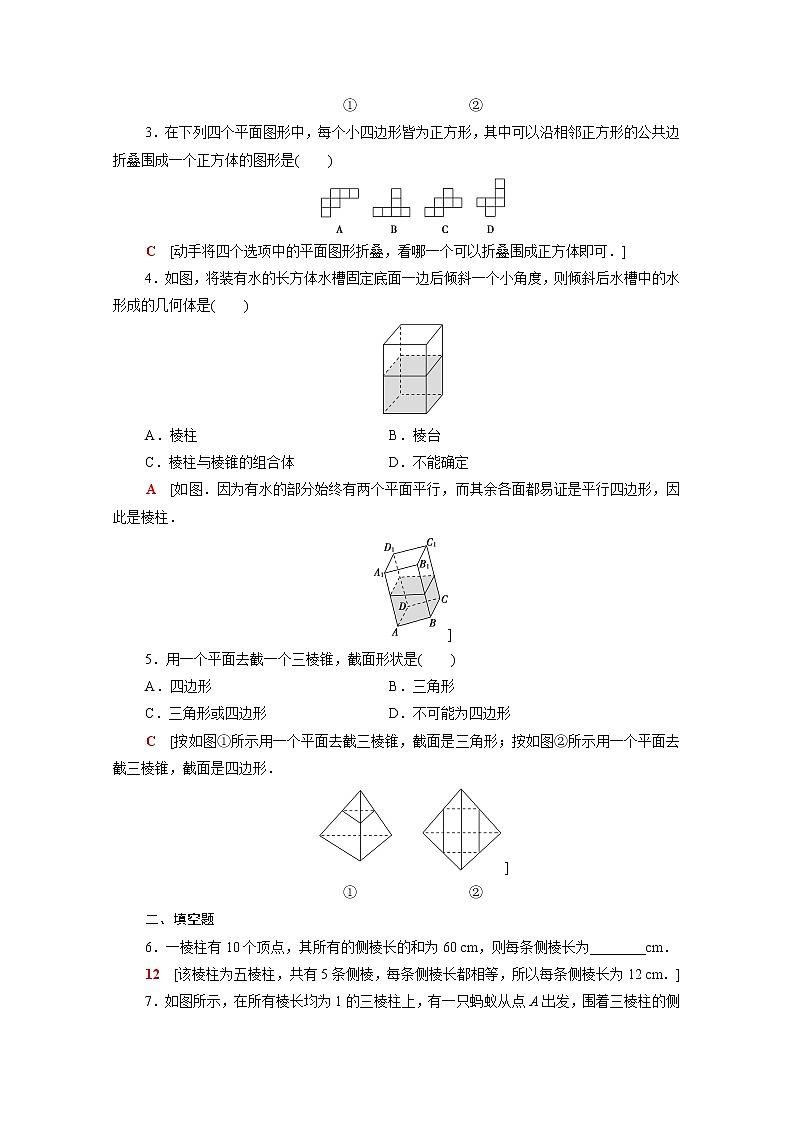
2．(多选题)下列说法错误的是( )
A．有2个面平行，其余各面都是梯形的几何体是棱台
B．多面体至少有3个面
C．各侧面都是正方形的四棱柱一定是正方体
D．九棱柱有9条侧棱，9个侧面，侧面为平行四边形
ABC [选项A错误，反例如图①；一个多面体至少有4个面，如三棱锥有4个面，不存在有3个面的多面体，所以选项B错误；选项C错误，反例如图②，上、下底面是全等的菱形，各侧面是全等的正方形，它不是正方体；根据棱柱的定义，知选项D正确．
]
① ②
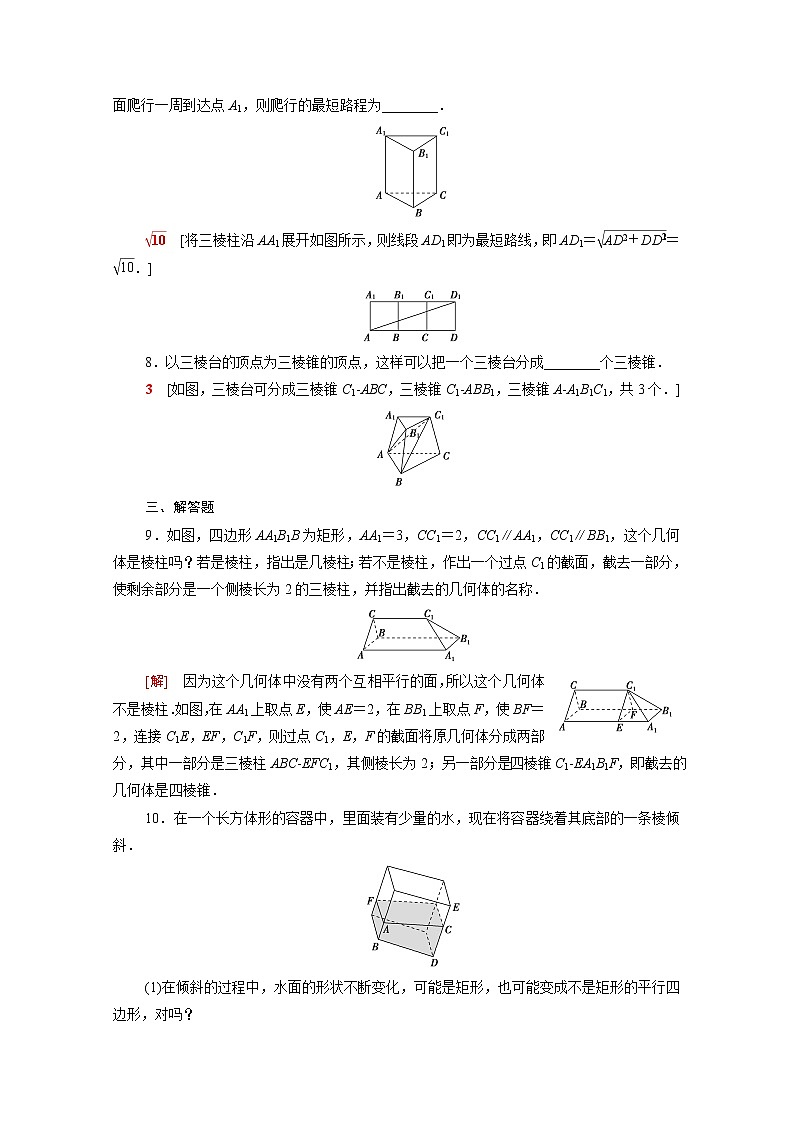
3．在下列四个平面图形中，每个小四边形皆为正方形，其中可以沿相邻正方形的公共边折叠围成一个正方体的图形是( )
C [动手将四个选项中的平面图形折叠，看哪一个可以折叠围成正方体即可．]
4．如图，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是( )
A．棱柱 B．棱台
C．棱柱与棱锥的组合体 D．不能确定
A [如图．因为有水的部分始终有两个平面平行，而其余各面都易证是平行四边形，因此是棱柱．
]
5．用一个平面去截一个三棱锥，截面形状是( )
A．四边形 B．三角形
C．三角形或四边形 D．不可能为四边形
C [按如图①所示用一个平面去截三棱锥，截面是三角形；按如图②所示用一个平面去截三棱锥，截面是四边形．
]
① ②
二、填空题
6．一棱柱有10个顶点，其所有的侧棱长的和为60 cm，则每条侧棱长为________cm．
12 [该棱柱为五棱柱，共有5条侧棱，每条侧棱长都相等，所以每条侧棱长为12 cm．]
7．如图所示，在所有棱长均为1的三棱柱上，有一只蚂蚁从点A出发，围着三棱柱的侧面爬行一周到达点A1，则爬行的最短路程为________．
eq \r(10) [将三棱柱沿AA1展开如图所示，则线段AD1即为最短路线，即AD1＝eq \r(AD2＋DD\\al(2,1))＝eq \r(10)．]
8．以三棱台的顶点为三棱锥的顶点，这样可以把一个三棱台分成________个三棱锥．
3 [如图，三棱台可分成三棱锥C1­ABC，三棱锥C1­ABB1，三棱锥A­A1B1C1，共3个．]
三、解答题
9．如图，四边形AA1B1B为矩形，AA1＝3，CC1＝2，CC1∥AA1，CC1∥BB1，这个几何体是棱柱吗？若是棱柱，指出是几棱柱；若不是棱柱，作出一个过点C1的截面，截去一部分，使剩余部分是一个侧棱长为2的三棱柱，并指出截去的几何体的名称．
[解] 因为这个几何体中没有两个互相平行的面，所以这个几何体不是棱柱．如图，在AA1上取点E，使AE＝2，在BB1上取点F，使BF＝2，连接C1E，EF，C1F，则过点C1，E，F的截面将原几何体分成两部分，其中一部分是三棱柱ABC­EFC1，其侧棱长为2；另一部分是四棱锥C1­EA1B1F，即截去的几何体是四棱锥．
10．在一个长方体形的容器中，里面装有少量的水，现在将容器绕着其底部的一条棱倾斜．
(1)在倾斜的过程中，水面的形状不断变化，可能是矩形，也可能变成不是矩形的平行四边形，对吗？
(2)在倾斜的过程中，水的形状也不断变化，可能是棱柱，也可能变为棱台或棱锥，对吗？
(3)如果倾斜时，不是绕着底部的一条棱，而是绕着其底面的一个顶点，上面的第(1)问和第(2)问对不对？
[解] (1)不对．水面的形状就是用一个与棱(长方体形容器倾斜时固定不动的棱)平行的平面截长方体时截面的形状，该截面的形状一定是矩形．
(2)不对．水的形状就是用与棱(长方体形容器倾斜时固定不动的棱)平行的平面将长方体截去一部分后，剩余几何体的形状，剩余几何体一定是棱柱，水比较少时，是三棱柱，水比较多时，可能是四棱柱或五棱柱，但不可能是棱台或棱锥．
(3)用任意一个平面去截长方体，其截面形状可以是三角形、四边形、五边形或六边形，因而水面的形状可以是三角形、四边形、五边形或六边形；水的形状可能是棱锥，也可能是棱柱，但不可能是棱台．故(1)对，(2)不对．
1．由五个面围成的多面体，其中上、下两个面是相似三角形，其余三个面都是梯形，并且这些梯形的腰延长后能相交于一点，则该多面体是( )
A．三棱柱 B．三棱台 C．三棱锥 D．四棱锥
B [该多面体有三个面是梯形，而棱锥最多有一个面是梯形(底面)，棱柱最多有两个面是梯形(底面)，所以该多面体不是棱柱、棱锥，而是棱台．三个梯形是棱台的侧面，另两个三角形是底面，所以这个棱台是三棱台．]
2．如图所示都是正方体的表面展开图，还原成正方体后，其中两个完全一样的是( )
① ② ③ ④
A．①② B．②③ C．③④ D．①④
B [在图②③中，⑤不动，把图形折起，则②⑤为对面，①④为对面，③⑥为对面，故图②③完全一样，而图①④则不同．]
3．五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个五棱柱的对角线共有________条．
10 [在上底面选一个顶点，同时在下底面选一个顶点，且这两个顶点不在同一侧面上，这样上底面每个顶点对应两条对角线，所以共有10条．]
4．试从正方体ABCD­A1B1C1D1的八个顶点中任取若干，连接后构成以下空间几何体，并且用适当的符号表示出来．
(1)只有一个面是等边三角形的三棱锥；
(2)四个面都是等边三角形的三棱锥；
(3)三棱柱．
[解] (1)如图①所示，三棱锥A1­AB1D1(答案不唯一)．
(2)如图②所示，三棱锥B1­ACD1(答案不唯一)．
(3)如图③所示，三棱柱A1B1D1­ABD(答案不唯一)．
① ②
③
如图，在长方体ABCD­A1B1C1D1中，AB＝3，BC＝4，A1A＝5，现有一只甲壳虫从点A出发沿长方体表面爬行到点C1来获取食物，试画出它的最短爬行路线，并求其路程的最小值．
[解] 把长方体的部分面展开，如图，有三种情况．
对甲、乙、丙三种展开图利用勾股定理可得AC1的长分别为eq \r(90)，eq \r(74)，eq \r(80)，由此可见乙是最短线路，所以甲壳虫可以先在长方形ABB1A1内由A到E，再在长方形BCC1B1内由E到C1，也可以先在长方形AA1D1D内由A到F，再在长方形DCC1D1内由F到C1，其最短路程为eq \r(74)．