初中数学5 二次函数与一元二次方程备课ppt课件

这是一份初中数学5 二次函数与一元二次方程备课ppt课件，共30页。PPT课件主要包含了教学目标，x2－x－1，x2－x等内容，欢迎下载使用。

1．会利用二次函数的图象求一元二次方程的近似根；2．进一步体会二次函数与一元二次方程的关系。
1.会用二次函数图象求一元二次方程的近似解及一元二次不等式的解集。
1.研究二次函数与一元二次方程的联系体会数形结合思想的应用。
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗？
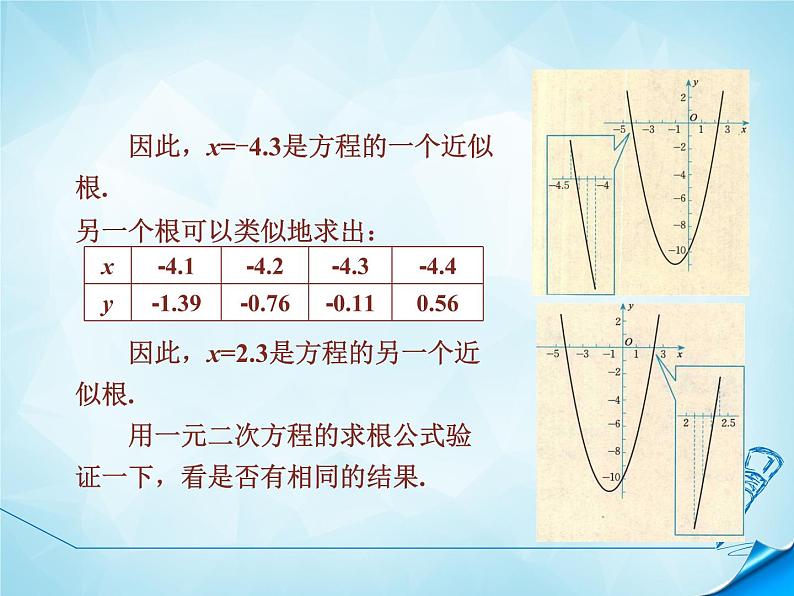
如图是函数y=x2+2x-10的图象.由图象可知方程有两个根，一个在-5和-4之间，另一个在2和3之间. (1)先求-5和-4之间的根.利用计算器进行探索：
因此，x=-4.3是方程的一个近似根.另一个根可以类似地求出： 因此，x=2.3是方程的另一个近似根. 用一元二次方程的求根公式验证一下，看是否有相同的结果.
利用二次函数的图象求一元二次方程的近似根的一般步骤：(1)画出二次函数y＝ax2＋bx＋c的图象；(2)确定二次函数的图象与x轴交点的个数，看交点的横坐 标在哪两个整数之间；
(3)列表，在两个整数之间取值，并用计算器算出对应的 y值，当x由x1变到x2，对应的y值出现y1＞0，y2＜0(或 y1＜0，y2＞0)且|y1|≠|y2|时，x1，x2中必有一个是方程 的近似根，再比较|y1|和|y2|，若|y1|＜|y2|，则x1是方程 的近似根；若|y1|＞|y2|，则x2是方程的近似根．
导引：当 y＝－x2＋2x－3的函数值为－8时，对应点的横 坐标即为一元二次方程－x2＋2x－3＝－8的根，如 图所示．
例1 利用二次函数的图象求一元二次方程－x2＋2x－ 3＝－8的近似根．
解：在平面直角坐标系内作函数y＝－x2＋2x－3的图象，如图， 由图象可知方程－x2＋2x－3＝－8的根是抛物线y＝－x2＋ 2x－3与直线y＝－8的公共点的横坐标，左边的公共点横坐 标在－1与－2之间，右边的公共点横坐标在3和4之间． (1)先求在－1和－2之间的根，利用计算器进行探索： 因此x＝－1.4是方程－x2＋2x－3＝－8的一个近似根．
(2)另一根可以类似地求出： 因此x＝3.4是方程－x2＋2x－3＝－8的另一个近似根．
解：先把方程化成x2＝－2x＋3. 如图，在同一直角坐标系中 分别画出函数y＝x2和 y＝－2x＋3的图象，得到它 们的交点为(－3，9)和(1，1)， 则方程x2＋2x－3＝0的解为x＝－3或x＝1.
例2 利用函数的图象，求方程x2＋2x－3＝0的根．
利用图象交点法求一元二次方程的根的步骤：(1)将ax2＋bx＋c＝0化为ax2＝－bx－c的形式；(2)在同一坐标系中画出y＝ax2与y＝－bx－c的图象；(3)观察图象：两图象的公共点情况即为方程的根的情 况，如有公共点，则公共点的横坐标即为ax2＋bx＋ c＝0的根．
【中考·包头】已知一次函数y1＝4x，二次函数y2＝2x2＋2，在实数范围内，对于x的同一个值，这两个函数所对应的函数值分别为y1与y2，则下列关系正确的是(　　)A．y1＞y2　 　B．y1≥y2　　C．y1＜y2　　 D．y1≤y2
小明在复习数学知识时，针对“求一元二次方程的解”总结了以下几种方法，请你将有关内容补充完整．例题：求一元二次方程x2－x－1＝0的两个解．(1)解法一：选择一种合适的方法(公式法、配方法、 因式分解法)求解．
(1)公式法： ∵a＝1，b＝－1，c＝－1， ∴Δ＝b2－4ac＝(－1)2－4×1×(－1)＝5＞0. ∴ 即x1＝ x2＝ .
(2)解法二：利用二次函数图象与x轴的交点求解．如 图①，把方程x2－x－1＝0的解看成是二次函数y ＝__________的图象与x 轴交点的横坐标x1，x2， 则x1，x2就是方程的解．
(3)解法三：利用两个函数图象的交点求解． ①把方程x2－x－1＝0的解看成是二次函数y＝ ________的图象与直线 y＝_______的交点的横坐标； ②在图②中画出这两个函数 的图象，用x1，x2在x轴上 标出方程的解．
根据图象可直观地回答使得y的值大于、等于或小于零时x的取值(范围)，具体如下表所述：
例3 画出抛物线y＝－x2＋4x＋5，观察抛物线，回答下 列问题： (1)x为何值时，函数值y＞0? (2)x为何值时，函数值y＝0? (3)x为何值时，函数值y＜0?
导引：根据抛物线的简易画法，先确定顶点以及抛物线与x 轴和y轴的交点，当函数值y＞0时，对应图象上的点 在x轴上方；当函数值y＝0时，对应图象上的点位于 x轴上；当函数值y＜0时，对应图象上的点在x轴的 下方．
解：∵y＝－x2＋4x＋5＝－(x2－4x)＋5＝－(x2－4x＋4)＋9＝ －(x－2)2＋9.∴抛物线的顶点坐标 为(2，9)，对称轴为直线x＝2. 令－x2＋4x＋5＝0，即x2－4x－5＝ 0，∴x1＝5，x2＝－1.∴抛物线与x 轴的两个交点为(－1，0)，(5，0)． 令x＝0，则y＝5，即抛物线与y轴的 交点为(0，5)．由抛物线的对称性知抛物线上的另一点为 (4，5)．在坐标系中描出各点，并连线得到如图所示的图 象．观察图象会发现：(1)当－1＜x＜5时，函数值y＞0； (2)当x＝－1或x＝5时，函数值y＝0； (3)当x＜－1或x＞5时，函数值y＜0
(1)作抛物线y＝ax2＋bx＋c(b2－4ac＞0)一般采用“五点法”， 而这“五点”一般为抛物线顶点，与x轴的两交点，与y 轴的交点及它关于对称轴的对称点．(2)根据二次函数值的取值范围确定自变量的取值范围， 一般要画出二次函数的图象，观察图象解答，抛物线 在x轴上方的部分，对应的函数值大于0；抛物线在x 轴下方的部分，对应的函数值小于0；抛物线与x轴的 公共点，对应的函数值等于0.
例4 〈齐齐哈尔〉抛物线y＝ax2＋bx＋c(a≠0)的对称轴 为直线x＝－1，与x轴的一个交点A在(－3，0)和 (－2，0)之间，其部分图象如图所示，则下列结 论：①4ac－b2＜0；②2a－b＝0；③a＋b＋c＜0； ④点M(x1，y1)，N(x2，y2)在抛物线上，若x1＜x2， 则y1＜y2.正确结论 的个数是(　　) A．1 　B．2　　　 　 C．3　　D．4
导引：观察图象可知二次函数对应的一元二次方程有两个 不相等的实数解，所以Δ＝b2－4ac>0，即4ac－b2< 0，故①正确；因为抛物线的对称轴为直线x＝－1， 所以－ ＝－1，即b＝2a，2a－b＝0，故②正确； 由二次函数图象的对称性可知抛物线与x轴的另一 个交点位于(0，0)和(1，0)之间，所以当x＝1时，y ＜0，即a＋b＋c<0，故③正确；由于二次函数在对 称轴两侧的增减性不一样，当x1y2；当x1＜－1＜x2且－1－x1＝ x2－(－1)时，y1＝y2，所以④错误．所以此题正 确的结论有3个．故选C.
【中考·烟台】如图，已知顶点为(－3，－6)的抛物线y＝ax2＋bx＋c经过点(－1，－4)，则下列结论中错误的是(　　)A．b2＞4acB．ax2＋bx＋c≥－6C．若点(－2，m)，(－5，n) 在抛物线上，则m＞nD．关于x的一元二次方程ax2＋bx＋c＝－4的两根为 －5和－1
利用图象求一元二次方程的根的方法：直接画出二次函数y＝ax2＋bx＋c的图象，则图象与x轴交点的横坐标就是一元二次方程ax2＋bx＋c＝0的根．其步骤一般为(1)作出二次函数y＝ax2＋bx＋c的图象；(2)观察图象与x轴交点的个数；(3)若图象与x轴有交点，估计出图象与x轴交点的横坐标 即可得到一元二次方程的近似根．
用图象法求x2－x＋ ＝0的解．
易错点：不考虑方程根的情况盲目作图象而致错
画出抛物线y＝x2－x＋ (如图)．由图象可知抛物线与x轴的交点为( ，0)，所以原方程的解为x1＝x2＝