初中数学北师大版九年级下册3 垂径定理课堂教学课件ppt

这是一份初中数学北师大版九年级下册3 垂径定理课堂教学课件ppt，共23页。PPT课件主要包含了教学目标，教学重点，教学难点，垂径定理及其推论，在△OAA中，∵OAOA，又∵AA垂直CD，∴MAMA，平分弦，弦所对的两条弧等内容，欢迎下载使用。

1．理解垂径定理和推论的内容，并会证明，利用垂径定理解决与圆有关的问题；2．利用垂径定理及其推论解决实际问题。
1.垂直于弦的直径的性质和推论。
1.运用垂径定理解决有关圆的问题。
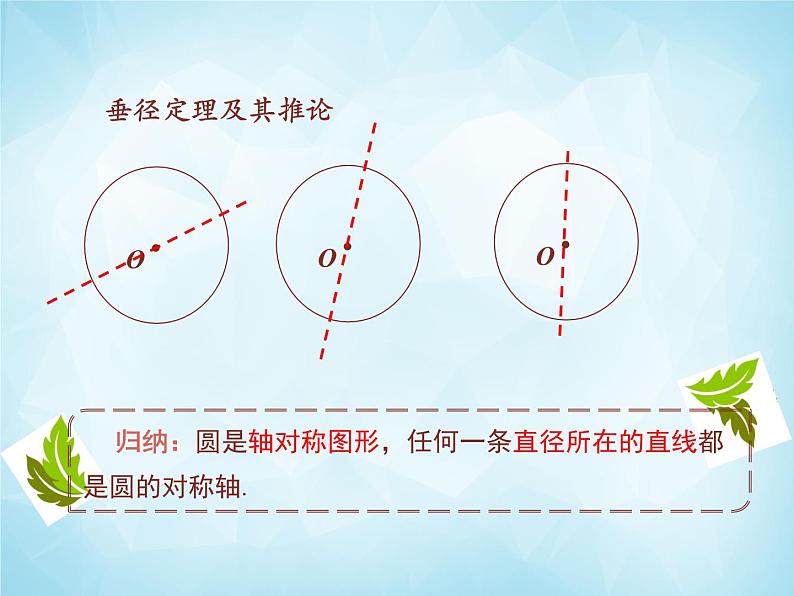
看一看：观察下图中图形的变化，试着发现它们的规律。
问题1：剪一个圆形纸片，沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得出什么结论？你能证明你的结论吗？
证明 设CD是⊙O的任意一条直径，A为⊙O上的点CD以外的任意一点.
过A作AA'垂直CD，交于⊙O点A'，垂足为M，连接OA，OA'.
∴△OAA'是等腰三角形.
即CD是AA'的垂直平分线.
从上面的证明过程中我们可以知道：
解 如图，用AB表示主桥拱，设AB所在圆的圆心为O，半径为R.
经过圆心O作弦AB的垂线OC垂足为D，与弧AB交于点C，则D是AB的中点，C是弧AB的中点，CD就是拱高.
由题设可知AB=37 ，CD=7.23 .
在Rt△OAD中，由勾股定理，得
OA2=AD2+OD2
解得R≈27.3（m）.
因此，赵州桥主桥拱半径约为27.3m.
2.如图，⊙O的弦AB=8，半径ON交AB于点M，M是AB的中点，且OM=3，则MN的长为（ ）
3.《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译文：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸），问这块圆柱形木材的直径是多少？如图，请根据所学的知识计算：圆柱形木材的直径AC是（ ）A.13寸 B.20寸C.26寸 D.28寸
4.如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为13，则点P的坐标为________.
5.如图，⊙O的直径为10，弦AB长为8，点P在AB上运动，则OP的最小值是________.
6.如图，直径AB垂直于弦CD于点E，CD=4，AE=8，⊙O的半径长为________.
7.如图，有一个拱桥是圆弧形，它的跨度为60 m，拱高为18 m，求拱桥的半径.
解 设圆弧的圆心为点O，过点O作OD⊥AB，交AB于点D，交圆弧于点E，
设拱桥的半径为x m，
则(x-18)2+302=x2,
即拱桥的半径为34 m.
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
平分弦（不是直径）的直径垂直于弦,并且平分弦所对的弧.