




2021学年3.2 勾股定理的逆定理课文配套ppt课件
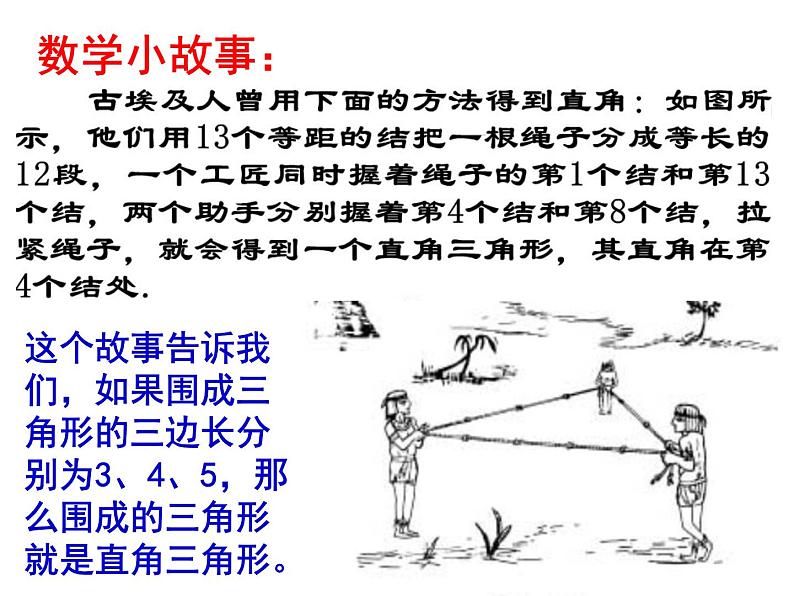
展开这个故事告诉我们,如果围成三角形的三边长分别为3、4、5,那么围成的三角形就是直角三角形。
A:3、4、3; B:3、4、5;C:3、4、6; D:6、8、10;
测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下: A:________ B:________ C:________ D:________
画图:画出边长分别是下列各组数的三角形。(单位:厘米)
判断:请判断一下上述你所画的三角形的形状。 A:_____________ B:____________ C:_____________ D:____________
找规律:根据上述每个三角形所给的各组边长,请你找出最长边的平方与其他两边的平方和之间的关系。
A:3、4、3; B:3、4、5; C:3、4、6; D:6、8、10;
A、锐角三角形B、直角三角形C、钝角三角形D、直角三角形
猜想:一个三角形各边长数量应满足怎样的关系式时,这个三角形才可能是直角三角形呢?
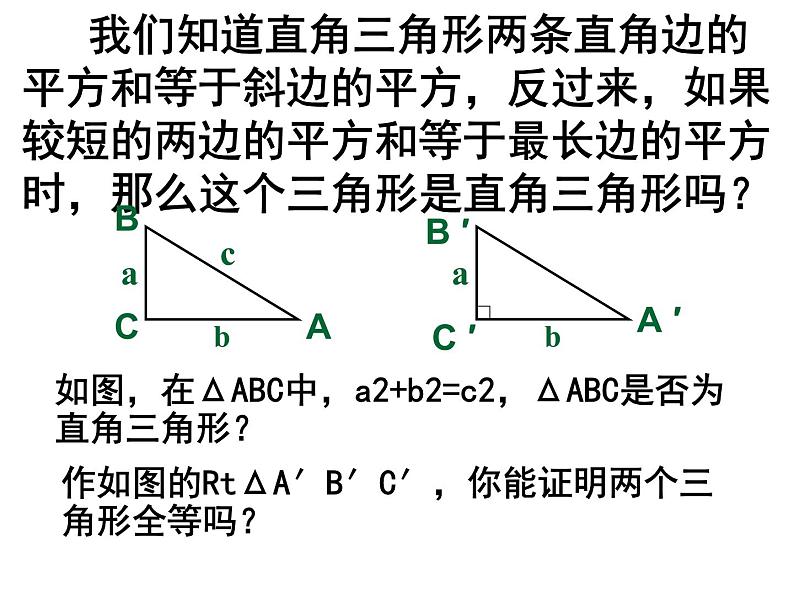
我们知道直角三角形两条直角边的平方和等于斜边的平方,反过来,如果较短的两边的平方和等于最长边的平方时,那么这个三角形是直角三角形吗?
如图,在ΔABC中,a2+b2=c2,ΔABC是否为直角三角形?
作如图的RtΔA′B′C′,你能证明两个三角形全等吗?
如果三角形的三边长a 、 b 、 c满足 , 那么这个三角形是直角三角形。
与勾股定理比较: 如果直角三角形的两直角边长分别a 、 b ,斜边长为 c,那么 。
如果三角形的三边长a,b,c有关系
这也是判定直角三角形的一种方法。
如果三条线段a、b、c满足c2=a2-b2,这三条线段组成的三角形是直角三角形吗?为什么?
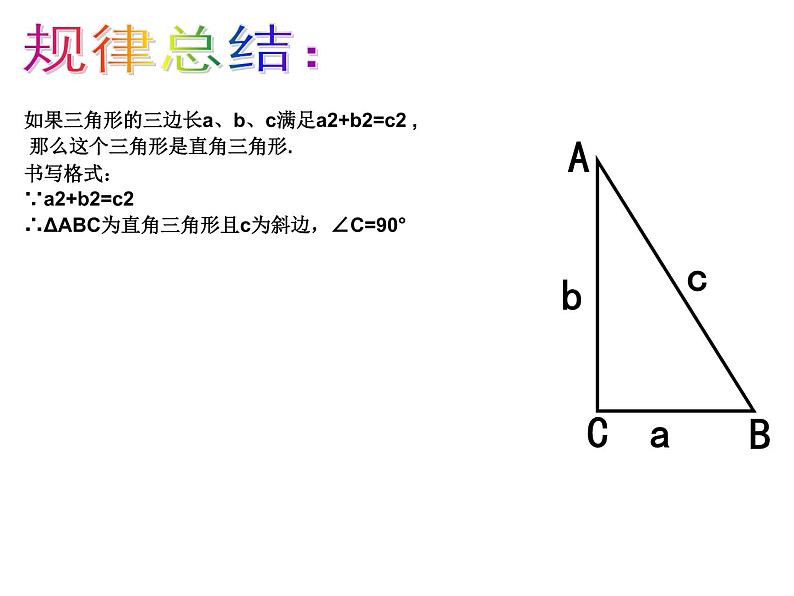
如果三角形的三边长a、b、c满足a2+b2=c2 , 那么这个三角形是直角三角形.书写格式:∵a2+b2=c2 ∴ΔABC为直角三角形且c为斜边,∠C=90°
例1 判断由线段a、b、c 组成的三角形是不是直角三角形: a=10, b=8, c=6 (2) a=1, b= , c= (3) a=13, b=14,c=15
步骤:1.确定最长边2.计算最长边的平方是否等于较短两边平方和3.判断是否为直角三角形
像 3,4,5;6,8,10;5,12,13等满足a2+b2=c2的一组正整数,通常称为勾股数。
利用勾股数可以构造直角三角形。
2.满足a2+b2=c2(c为最大数)
(2)从上表中你能发现什么规律?
(3)你能根据发现的规律,写出更多的勾股数吗?试试看!
如果一组勾股数都分别扩大相同的整数倍,那么得到的仍是一组勾股数.
若下表中的a、b、c为勾股数.(1)填表:
(2)12,16,20 (3)15,20,25(4)50,120,130
练一练1:下列各组数是勾股数吗?能构造直角三角形吗?(1)30,40,50
判断是否为勾股数的方法:·看是否为正整数,是否满足a2+b2=c2(c为最大数)
·看是否为已知勾股数的整数倍
例2 已知:在△ABC中,三条边分别为a,b,c,a=n2-1,b=2n,c=n2+1(n>1).试说明∠C=90°
∵a2+b2=(n2-1)2+(2n)2
∵c-b=n2+1-2n
∵ n2+1>n2-1
=n4-2n2+1+4n2
例3 一个零件的形状如图,按规定这个零件中∠A 与∠DBC都应为直角,工人师傅量得零件各边尺寸:AD = 4,AB = 3, BC = 12 , DC=13,BD=5,你能根据所给的数据说明这个零件是否符合要求吗?
∵AD=4,AB=3,BD=5
∴AD2+AB2=BD2
∵BD=5,BC=12,CD=13
∴BD2+BC2=CD2
(1)已知在四边形ABCD中, ∠A=90°,AB=3,BC=12,CD=13,DA=4,试说明BD⊥BC
∵∠A=90°,AB=3,AD=4
∵CD=13,BC=12
(2) 在△ABC中,D是BC边上的一点,AB=15,AC=13,AD=12,CD=5,求BC的长.
∵AC=13,AD=12,CD=5
∴CD2+AD2=AC2
∵AB=15,AD=12
∴BC=BD+DC=9+5=14
已知:如图,在△ABC中,D是BC中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2.试说明∠A=90°
∵D是BC中点,DE⊥BC
∵BE2-EA2=AC2
∴EC2-EA2=AC2
∴ED是BC的垂直平分线
通过本节课的学习,你知道一个三角形的三边在数量上满足怎样的关系时,这个三角形才是直角三角形呢?
1.完成创新导学手册P48-49页的训练与提高
2.了解古巴比伦“普林顿322” 泥板中的神秘的数组
美国哥伦比亚大学图书馆收藏着一块编号为“普林顿322” (plinmptn322)的古巴比伦泥板,上面密密麻麻的写着什么呢?
苏科版3.2 勾股定理的逆定理优质ppt课件: 这是一份苏科版3.2 勾股定理的逆定理优质ppt课件,共39页。PPT课件主要包含了解法提醒,特别提醒,勾股定理的逆定理,2练习,解都是勾股数,解是直角三角形等内容,欢迎下载使用。
初中数学苏科版八年级上册3.2 勾股定理的逆定理课前预习课件ppt: 这是一份初中数学苏科版八年级上册3.2 勾股定理的逆定理课前预习课件ppt,文件包含32勾股定理的逆定理pptx、32勾股定理的逆定理docx等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
苏科版八年级上册3.2 勾股定理的逆定理课前预习ppt课件: 这是一份苏科版八年级上册3.2 勾股定理的逆定理课前预习ppt课件,共49页。PPT课件主要包含了勾股定理的逆定理,第一课时,学习目标,互逆命题,三角形全等,∴ABc,综合应用,命题和逆命题,勾股数,误区诊断等内容,欢迎下载使用。













