数学九年级下册5.1 二次函数备课课件ppt

这是一份数学九年级下册5.1 二次函数备课课件ppt，共19页。PPT课件主要包含了1二次函数，Sπr2，yx8-x，新知探索，a≠0，y-x2+8x，概念教学，二次函数的概念，反馈练习，先化简后判断等内容，欢迎下载使用。

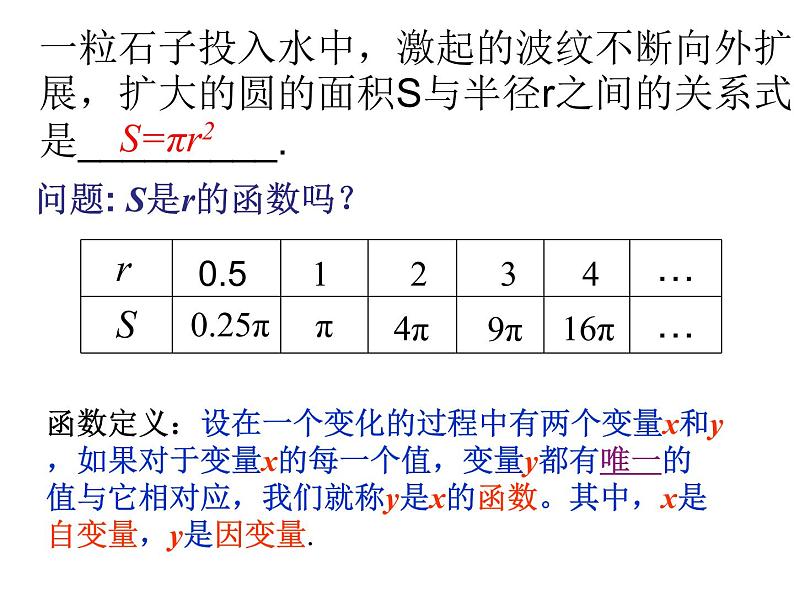
1、一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S与半径r之间的关系式是_________.
一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S与半径r之间的关系式是_________.
问题: S是r的函数吗？
函数定义：设在一个变化的过程中有两个变量x和y ，如果对于变量x的每一个值，变量y都有唯一的值与它相对应，我们就称y是x的函数。其中，x是自变量，y是因变量.
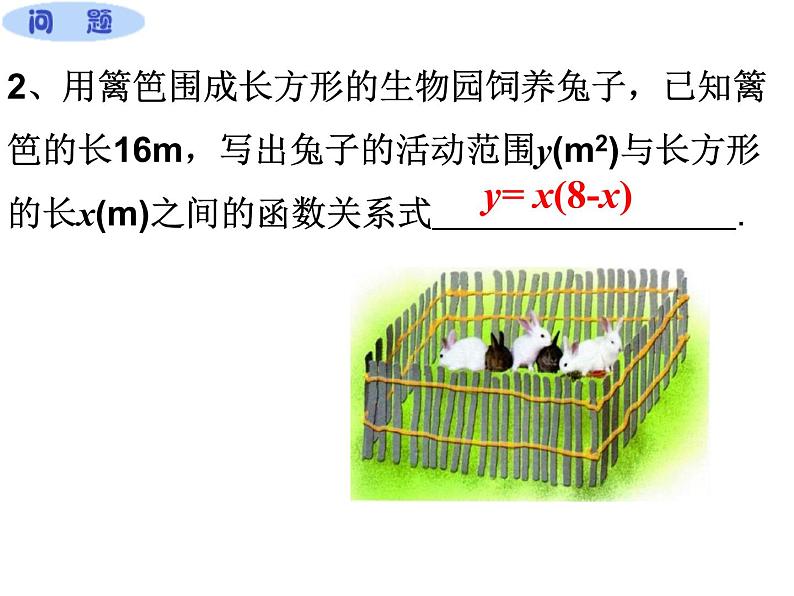
2、用篱笆围成长方形的生物园饲养兔子，已知篱笆的长16m，写出兔子的活动范围y(m2)与长方形的长x(m)之间的函数关系式 .
3 、要给一个边长为x m的正方形房间铺设地板，已知某种地板的价格为每平方米240元，踢脚线价格为每米30元，如果其它费用为1000元，门宽0.8米，那么总费用y为多少元？
y=240x2+30(4x-0.8)+1000
上述问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax²+bx+c 的形式.
(a,b,c是常数, )
（1）关系式都是整式，（2）自变量的最高次数是二次，（3）二次项系数不等于零.
y=240x2+120x+976
一般地，我们称形如y=ax²+bx+c (a,b,c是常数, a≠0 )的函数为二次函数，其中x是自变量，y是x的函数。
例1、下列函数中，哪些是二次函数？ (1)y=3x-1 ( ) (2)y=3x2 ( ) (3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( ) (5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )
(4)在y=ax2+bx+c (a≠0)中，x的取值范围是全体实数。
一般地，我们称形如y=ax²+bx+c (a,b,c是常数, a≠0 )的函数为二次函数，其中x是自变量，y是x的函数。
(1)关于自变量的代数式一定是二次整式.
(2)自变量的最高次数为2，可以没有一次项和常数项，但不能没有二次项。
(3)任何一个二次函数都可以化成y=ax2+bx+c(a≠0)的形式，因此，把它叫做二次函数的一般形式；
下列函数是否为二次函数，如果是，指出其中常数a、b、c的值.


例2．当k为何值时，函数 为二次函数？
判断是否为二次函数的关键：
最高次数是二次；二次项系数不能为零.
如果函数y= +kx+1是二次函数,则k的值一定是______
提醒：当自变量表示实际意义时，自变量的取值范围就不一定是全体实数。
y=ax²+bx+c (a,b,c是常数, a≠0 )
一般地，二次函数y=ax2 +bx+c中自变量x的取值范围是一切实数，但在实际问题中自变量会受到实际问题的限制，你能说出上述4个问题中自变量的取值范围吗？
2、用篱笆围成长方形的生物园饲养兔子，已知篱笆的长16m，写出兔子的活动范围y(m2)与长方形的长x(m)之间的函数关系式____________.
3、要给一个边长为x m的正方形房间铺设地板，已知某种地板的价格为每平方米240元，踢脚线价格为每米30元，如果其它费用为1000元，门宽0.8米，那么总费用y为多少元？
例3．写出下列各函数关系，并判断它们是什么类型的函数． ⑴正方体的表面积S（cm2）与棱长a（cm）之间的函数关系； ⑵圆的面积y（cm2）与它的周长x（cm）之间的函数关系； ⑶菱形的两条对角线的和为26cm，求菱形的面积S（cm2）与一对角线长x（cm）之间的函数关系．
定义中应该注意的几个问题:
1.定义：一般地,形如y= ax²+bx+c(a,b,c是常数, a≠0)的函数叫做x的二次函数.y=ax²+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:(1) y=ax²(a≠0, b=0, c=0,).(2)y=ax²+c (a≠0, b=0, c≠0).(3) y=ax²+bx(a≠0, b≠0, c=0). 2.定义的实质是：ax²+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.