2020-2021学年本节综合课后练习题

《11.3 多边形及其内角和》课时提升训练习题

2020-2021学年人教版数学八（上）

一．选择题（共11小题）

1．已知一个多边形的内角和是外角和的，则这个多边形的边数是（　　）

A．4 B．5 C．6 D．7

2．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（　　）

A．108° B．90° C．72° D．60°

3．一个多边形的内角和比它的外角和的2倍少180°，这个多边形的边数是（　　）

A．5 B．6 C．7 D．8

4．若一个正多边形的每一个外角为30°，那么这个正多边形的边数是（　　）

A．6 B．8 C．10 D．12

5．如图在五边形ABCDE中，∠A＝∠B＝∠C＝∠D，∠DEF＝3∠AEF（　　）

A．45° B．60° C．72° D．无法确定

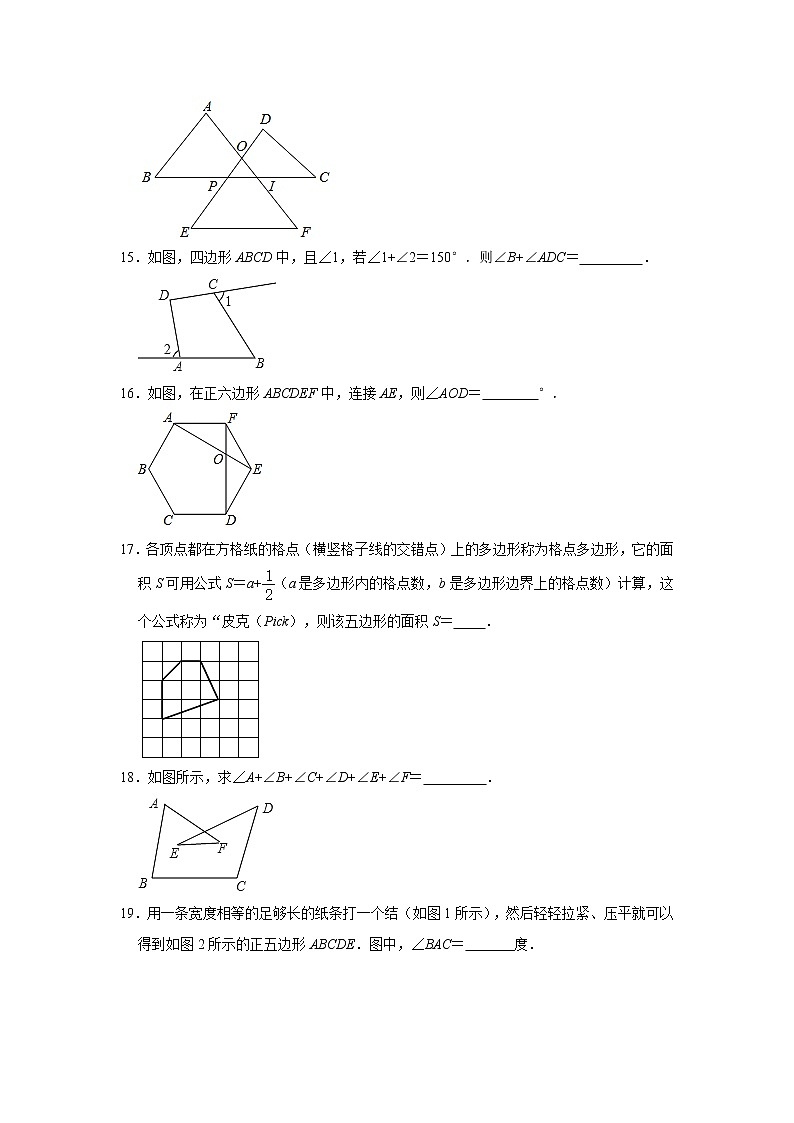
6．如图为二环四边形，它的内角和∠A+∠B+∠C+∠D+∠A1+∠B1+∠C1+∠D1度数为（　　）

A．360° B．540° C．720° D．900°

7．如图，已知△ABC为直角三角形，∠C＝90°，则∠1+∠2＝（　　）

A．90° B．135° C．270° D．315°

8．如图，已知∠1＝40°，∠A+∠B＝140°（　　）

A．40° B．60° C．80° D．100°

9．如图，小林从P点向西直走12米后，向左转，再走12米，如此重复，则α﹣5的值是（　　）

A．35° B．40° C．50° D．不存在

10．下列说法中错误的是（　　）

A．三角形的中线、角平分线、高都是线段 

B．任意三角形的内角和都是 180° 

C．多边形的外角和等于 360° 

D．三角形的一个外角大于任何一个内角

11．如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝n•90°，则n＝（　　）

A．5 B．6 C．7 D．8

二．填空题（共8小题）

12．一个n边形的各内角都等于120°，则边数n是　 　．

13．若一个多边形的内角和与外角和之和是1800°，则此多边形是　 　边形．

14．如图，∠A+∠B+∠C+∠D+E+∠F的度数为　     　．

15．如图，四边形ABCD中，且∠1，若∠1+∠2＝150°．则∠B+∠ADC＝　     　．

16．如图，在正六边形ABCDEF中，连接AE，则∠AOD＝　    　°．

17．各顶点都在方格纸的格点（横竖格子线的交错点）上的多边形称为格点多边形，它的面积S可用公式S＝a+（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克（Pick），则该五边形的面积S＝　 　．

18．如图所示，求∠A+∠B+∠C+∠D+∠E+∠F＝　     　．

19．用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE．图中，∠BAC＝　   　度．

三．解答题（共4小题）

20．（1）一个五角星ABCDE，如图（1）所示

（2）变式一：如果B点向下移动到AC上，如图（2）所示

（3）变式二：如果B点继续向下，移到AC的另一侧，如图（3），变式一中的结果还成立吗？

21．（1）如图1，△ABC中，∠ABC的平分线与外角∠ACD的平分线相交于P点，并说明理由．

（2）如图2、3，四边形ABCD中，设∠A＝α，∠P为四边形ABCD的内角∠ABC的平分线与外角∠DCE的平分线所在直线相交而形成的锐角．请利用（1）中的结论完成下列问题：

①如图2，若α+β＞180°，直接写出∠P的度数．（用α，β的代数式表示）

②如图3，若α+β＜180°，直接写出∠P的度数．（用α，β的代数式表示）

22．四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．

（1）若点O在四边形ABCD的内部，

①如图1，若AD∥BC，∠B＝40°，则∠DOE＝　    　°；

②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．

（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．

23．如图，求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数．

参考答案

一．选择题（共11小题）

1．解：设这个多边形是n边形，由题意得，

（n﹣2）•180°＝360°×，

解得n＝5，

故选：B．

2．解：设此多边形为n边形，

根据题意得：180（n﹣2）＝540，

解得：n＝5，

∴这个正多边形的每一个外角等于：＝72°．

故选：C．

3．解：设这个多边形为n边形，由题意得，

（n﹣2）×180°＝360°×2﹣180°，

解得n＝4，

即这个多边形为五边形，

故选：A．

4．解：这个正多边形的边数：360°÷30°＝12，

故选：D．

5．解：设∠A＝∠B＝∠C＝∠D＝x°，∠AEF＝y°，依题意有

4x+4y＝540，

解得x+y＝135，

则∠AFE＝180°﹣135°＝45°．

故选：A．

6．解：如图，

AA1之间添加两条边，可得B1+∠C8+∠D1＝∠EAD1+∠AEA2+∠EA1B1

则∠A+∠B+∠C+∠D+∠A2+∠B1+∠C1+∠D5＝∠EAB+∠B+∠C+∠D+∠DA1E+∠E＝720°；

故选：C．

7．解：∵∠C＝90°，

∴∠A+∠B＝90°．

∵∠A+∠B+∠1+∠2＝360°，

∴∠5+∠2＝360°﹣90°＝270°．

故选：C．

8．解：连接CD，如图：

∵∠1＝40°，∠1+∠5+∠3＝180°，

∴∠2+∠2＝180°﹣40°＝140°，

∵∠A+∠B+∠ADC+∠BCD＝360°，∠A+∠B＝140°，

∴∠ADC+∠BCD＝360°﹣140°＝220°，

∴∠BCE+∠ADE＝（∠ADC+∠BCD）﹣（∠2+∠3）＝220°﹣140°＝80°，

故选：C．

9．解：设边数为n，根据题意，

n＝108÷12＝9，

∴α＝360°÷9＝40°．

所以α﹣2＝35°，

故选：A．

10．解：A、三角形的中线、高线都是线段；

B、三角形的内角和为180°；

C、多边形的外角和等于，所以D选项的说法正确；

D、三角形的一个外角大于任何一个不相邻的内角．

故选：D．

11．解：连接BE，GE

．

∵∠1是△ADH的外角，

∴∠1＝∠A+∠D，

∵∠4是△JHG的外角，

∴∠1+∠G＝∠2，

∴在四边形BEFJ中，∠EBJ+∠BJF+∠EFJ+∠BEF＝360°…①，

在△BCE中，∠EBC+∠C+∠BEC＝180°…②，

①+②得，∠BEG+∠BGF+∠F+∠BEF+∠EBC+∠C+∠BEC＝360°+180°＝540°，

即∠A+∠B+∠C+∠D+∠E+∠F+∠G＝540°，

∴n＝＝2．

∴n＝6．

故选：B．

二．填空题（共8小题）

12．解：∵n边形的各内角都等于120°，

∴每一个外角都等于180°﹣120°＝60°，

∴边数n＝360°÷60°＝6．

故答案为：6．

13．解：∵多边形的一个内角与它相邻外角的和为180°，

∴1800°÷180°＝10．

故答案为：十．

14．解：∵∠AIC＝∠A+∠B，∠EPC＝∠C+∠D，

∴∠A+∠B+∠C+∠D+∠E+∠F＝∠AIC+∠EPC+∠AOE＝360°．

故答案为：360°．

15．解：∵∠1+∠2＝150°，

∴∠DAB+∠DCB＝360°﹣150°＝210°，

∵∠B+∠D+∠DAB+∠DCB＝360°，

∴∠B+∠ADC＝360°﹣（∠DAB+∠DCB）＝150°，

故答案为150°．

16．解：∵六边形ABCDEF是正六边形，

∴∠AFE＝∠DEF＝120°，AF＝EF＝DE，

∴∠FAE＝∠FEA＝∠EFD＝（180°﹣120°）÷2＝30°，

∴∠AFD＝120°﹣30°＝90°，

∴∠AOD＝∠FAE+∠AFD＝30°+90°＝120°．

故答案为：120．

17．解：a表示多边形内部的格点数，b表示多边形边界上的格点数，

通过图象可知a＝4，b＝6，

∴该五边形的面积S＝2+×8﹣1＝6，

故答案为：2．

18．解：如图，连接AD．

∵∠1＝∠E+∠F，∠1＝∠FAD+∠EDA，

∴∠E+∠F＝∠FAD+∠EDA，

∴∠A+∠B+∠C+∠D+∠E+∠F

＝∠BAD+∠ADC+∠B+∠C．

又∵∠BAD+∠ADC+∠B+∠C＝360°，

∴∠A+∠B+∠C+∠D+∠E+∠F＝360°．

故答案为：360°．

19．解：∵∠ABC＝＝108°，

∴∠BAC＝∠BCA＝36度．

三．解答题（共4小题）

20．解：（1）如图1，∵∠BKF＝∠C+∠E，

又∵∠B+∠BFK+∠BKFF＝180°，

∴∠A+∠B+∠C+∠D+∠E＝180°；

（2）如图2，∵∠A+∠C＝∠DFH，

又∵∠DFH+∠6+∠DHF＝180°，

∴∠A+∠C+∠DBE+∠E+∠D＝180°；

（3）如图3，∵∠B+∠D＝∠2，

由三角形内角和定理可知∠5+∠2+∠E＝180°，

即∠B+∠D+∠A+∠C+∠E＝180°，故结论都成立．

21．解：（1）2∠P＝∠A．

理由：∵∠PCD＝∠P+∠PBC，∠ACD＝∠A+∠ABC，

∵P点是∠ABC和外角∠ACD的角平分线的交点，

∴2∠PCD＝∠ACD，8∠PBC＝∠ABC，

∴2（∠P+∠PBC）＝∠A+∠ABC，

2∠P+5∠PBC＝∠A+∠ABC，

2∠P+∠ABC＝∠A+∠ABC，

∴2∠P＝∠A；

（2）①延长BA交CD的延长线于F，如图6，

∵∠F＝180°﹣∠FAD﹣∠FDA＝180°﹣（180°﹣α）﹣（180°﹣β）＝α+β﹣180°，

由（1）可知：∠P＝∠F，

∴∠P＝（α+β）﹣90°；

②如图3，延长AB交DC的延长线于F．

∵∠F＝180°﹣α﹣β，∠P＝，

∴∠P＝（180°﹣α﹣β）＝90°﹣．

22．解：（1）①∵AD∥BC，∠B＝40°，

∴∠BAD＝140°，∠ADC＝110°，

∵AE、DO分别平分∠BAD，

∴∠OAD＝70°，∠ADO＝55°，

∴∠DOE＝∠OAD+∠ADO＝70°+55°＝125°

故答案为：125；

②∠B+∠C+2∠DOE＝360°，

理由：∵∠DOE＝∠OAD+∠ADO，

∵AE、DO分别平分∠BAD，

∴2∠DOE＝∠BAD+∠ADC，

∵∠B+∠C+∠BAD+∠ADC＝360°，

∴∠B+∠C+4∠DOE＝360°；

（2）∠B+∠C＝2∠DOE，

理由：∵∠BAD+∠ADC＝360°﹣∠B﹣∠C，∠EAD+∠ADO＝180°﹣∠DOE，

∵AE、DO分别平分∠BAD，

∴∠BAD＝2∠EAD，∠ADC＝6∠ADO，

∴∠BAD+∠ADC＝2（∠EAD+∠ADO），

∴360°﹣∠B﹣∠C＝2（180°﹣∠DOE），

∴∠B+∠C＝2∠DOE．

23．解：如图所示，连接CG，

∵∠COG＝∠AOB，

∴∠6+∠7＝∠OCG+∠OGC，

又∵五边形CDEFG中，∠7+∠2+∠OCG+∠OGC+∠3+∠4+∠5＝540°，

∴∠1+∠3+∠6+∠7+∠8+∠4+∠5＝540°．