苏教版必修13.4.1 函数与方程教学设计

这是一份苏教版必修13.4.1 函数与方程教学设计，共4页。教案主要包含了教材分析，过程分析等内容，欢迎下载使用。

1.地位与作用
本节内容为苏教版版必修1第三章《指数函数、对数函数和幂函数》第四节《函数的应用》的第一课时《函数与方程》，主要内容是函数零点概念、函数零点与相应方程根的关系、函数零点存在性定理，是一节概念课．本节课不仅为二分法的学习做准备，而且为方程与函数提供了零点这个连接点，从而揭示了两者之间的本质联系，这种联系正是“函数与方程思想”的理论基础．用函数的观点研究方程，本质上就是将局部的问题放在整体中研究，将静态的结果放在动态的过程中研究，这为今后进一步学习函数与不等式等其它知识的联系奠定了坚实的基础。
2.教学目标：
（1）了解函数零点的概念：能够结合具体方程（如二次方程），说明方程的根、函数的零点、函数图象与x轴的交点三者的关系；
（2）理解函数零点存在性定理，利用函数图象判断函数在某区间上是否存在零点；
（3）经历“类比—归纳—应用”的过程，初步体会函数方程思想。
3. 教学重点：了解函数零点概念，掌握函数零点存在性定理。
4.教学难点：对零点存在性定理的准确理解。
二、过程分析
1.教学结构设计：
零点概念的建构
零点存在性定理的探究
创设情境，感知概念
辨析讨论，明确概念
实例尝试，归纳定理
辨析应用，熟悉定理
例题变式，深化拓展
应用与巩固
小结反思，提高认识
布置作业，独立探究
结课
2.教学过程设计：
（一）创设情境，感知概念
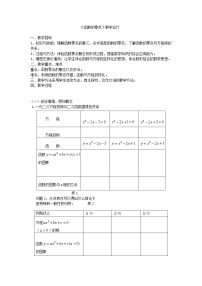
（1）一元二次方程的根与二次函数图象之间的关系．
填空：
问题1：从该表你可以得出什么结论？
归纳：
问题2：一元二次方程的根与相应的二次函数的图象之间有怎样的关系？
学生讨论，得出结论：一元二次方程的根就是函数图象与x轴交点的横坐标．
意图：通过回顾二次函数图象与轴的交点和相应方程的根的关系，为一般函数及相应方程关系作准备．
（2）一般函数的图象与方程根的关系．
问题3：其他的函数与方程之间也有类似的关系吗？为什么？
师生互动，在学生回答的基础上，老师加以改善，从而得出一般的结论：
方程有几个根，的图象与轴就有几个交点，且方程的根就是交点的横坐标．
意图：通过二次函数，将结论推广到一般函数，为零点概念做好铺垫．
（二）辨析讨论，深化概念．
（1）函数零点．
概念：一般地，我们把使函数的值为的实数称为的零点．
说明：①函数的零点就是方程的根；
函数的零点就是其图象与轴交点的横坐标．
②函数零点不是一个点，而是具体的自变量的取值．
③零点对于函数而言，根对于方程而言．
例1．写出下列函数的零点：
（1）；（2）；（3）．
设计意图：函数零点的解法，求相应方程的实数根．复习前面学习的二次方程，对数方程，指数方程，并体会方程的根与相应函数零点之间的密切联系．
（三）实例探究，归纳定理．辨析应用，熟悉定理．
例2．判断函数在区间上是否存在零点．
设计意图：判断函数在区间上是否存在零点．
通过对例2的研究发现两种处理方法：法一：用方程的思想解决函数零点问题
法二：利用函数图像解决零点存在性问题，并通过归纳得出零点存在性定理．
判断连续函数在区间上有零点的一个方法：
若函数在区间上的图象是一条不间断的曲线，且，则函数在区间上有零点.
说明：（1），题中为什么区间不统一，反例
（2）该结论无法确定零点的个数，通过画图说明，并说明函数在区间上有零点，不能得到
例3．求证：函数在区间上存在零点．
例3设计意图：简单运用零点存在性定理．
（四）综合应用，拓展思维．
例4. 判断函数是否存在零点．
例4设计意图：函数图像不熟悉，而且没有给出区间，怎么判断零点是否存在？灵活运用零点存在性定理找到零点存在区间。为下节课的二分法找到零点存在区间。
（五）总结整理，提高认识．
（1）一个关系：函数零点与方程根的关系：
函数
方程
零点
根
数 值
存在性
个 数
（2）两种思想：函数方程思想；数形结合思想．
（3）三种题型：求函数零点、判断零点是否存在、求二次方程区间根问题．
（七）布置作业，独立探究．方程
根
无实数根
函数
图象
4
2
-2
-4
3
-1
1
2
O
x
y
4
2
-2
-4
3
-1
1
2
O
x
y
4
2
-2
3
-1
1
2
O
x
y
图象与x轴的交点
两个交点：
(-1,0)，(3,0)
一个交点：(1,0)
没有交点
判别式Δ
Δ＞0
Δ＝0
Δ＜0
的根
两个不相等的实数根
有两个相等的
实数根
没有实数根
的图象
O
x
y
x1
x2
O
y
x
x1
O
x
y
函数的图象与x轴的交点
两个交点：
一个交点：
无交点