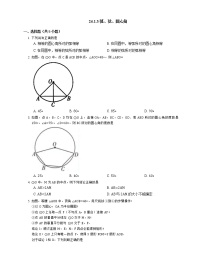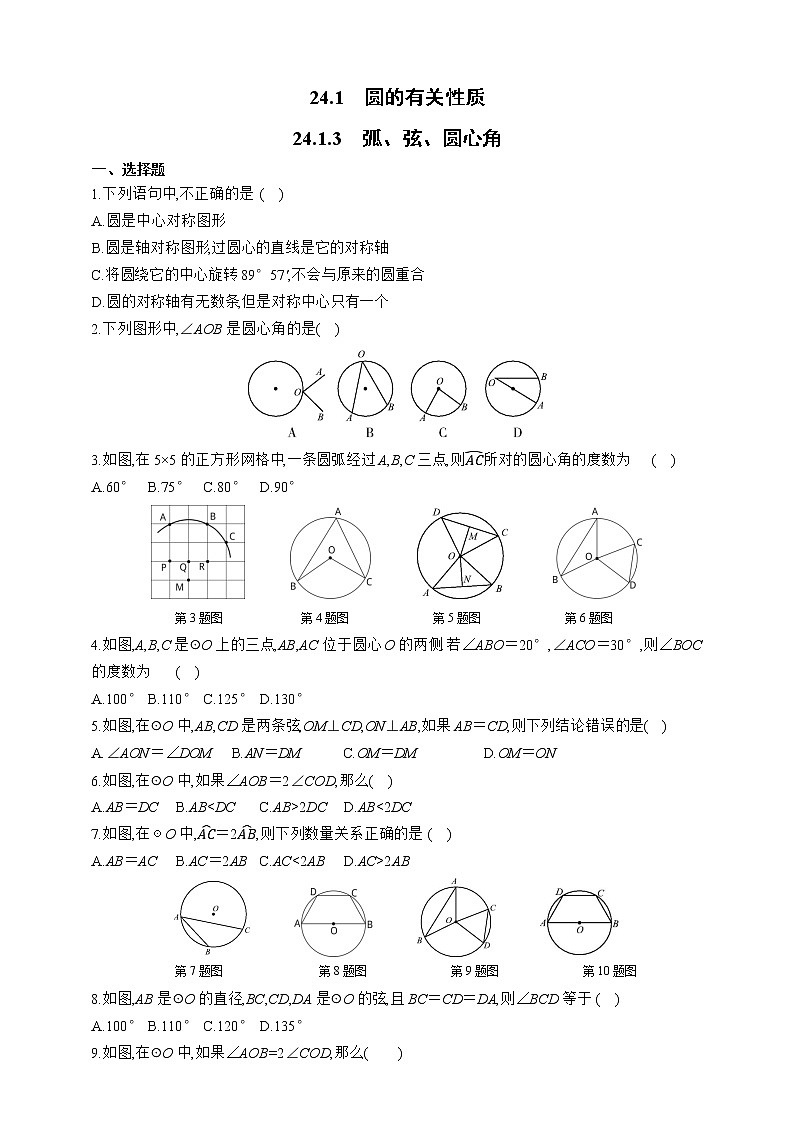
人教版九年级上册24.1.3 弧、弦、圆心角同步练习题

这是一份人教版九年级上册24.1.3 弧、弦、圆心角同步练习题，共13页。试卷主要包含了下列语句中,不正确的是等内容，欢迎下载使用。

一、选择题
1.下列语句中,不正确的是( )
A.圆是中心对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.将圆绕它的中心旋转89°57',不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
2.下列图形中,∠AOB是圆心角的是( )
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,则AC所对的圆心角的度数为( )
A.60°B.75°C.80°D.90°

第3题图 第4题图 第5题图 第6题图
4.如图,A,B,C是☉O上的三点,AB,AC位于圆心O的两侧.若∠ABO＝20°,∠ACO＝30°,则∠BOC的度数为( )
A.100°B.110°C.125°D.130°
5.如图,在☉O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB＝CD,则下列结论错误的是( )
A.∠AON＝∠DOMB.AN＝DMC.OM＝DMD.OM＝ON
6.如图,在☉O中,如果∠AOB＝2∠COD,那么( )
A.AB＝DCB.AB2DCD.AB<2DC
7.如图,在☉O中,AC＝2AB,则下列数量关系正确的是( )
A.AB＝ACB.AC＝2ABC.AC<2ABD.AC>2AB

第7题图 第8题图 第9题图 第10题图
8.如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC＝CD＝DA,则∠BCD等于( )
A.100°B.110°C.120°D.135°
9.如图,在☉O中,如果∠AOB=2∠COD,那么( )
A.AB=DCB.ABC.AB>2DCD.AB<2DC
10.如图，AB是⊙O的直径，点C，D在⊙O上，四边形ABCD中，BC＝CD＝DA＝4cm，则⊙O的周长为( )
A.5π cmB.6π cmC.7π cmD.8π cm
11.如图，AB，CD分别为⊙O的两条弦，OM⊥AB于点M，ON⊥CD于点N，且∠AOB＝∠COD，则下列结论：
①AB＝CD；
②OM＝ON；
③AB＝CD.
其中正确的个数为( )
A．0 B．1 C．2 D．3

第11题图 第12题 第13题图 第14题图
12.如图，在⊙O中，∠AOB＝2∠COD，则AB与2CD的大小关系是( )
A. AB＝2CD B. AB＞2CD
C. AB＜2CD D.不能确定
13.如图，在⊙O中，AB＝CD，则下列结论：
①AB＝CD；
②AC＝BD；
③∠AOC＝∠BOD；
④AC＝BD.
其中正确的个数是( )
A．1 B．2 C．3 D．4
14.(中考·兰州)如图，在⊙O中，点C是AB的中点，∠A＝50°，则∠BOC等于( )
A．40° B．45° C．50° D．60°
15.如图，△ABC的各顶点都在⊙O上，D，E，F是三边的中点，若AB＝AC，则四边形AEDF的形状是( )
A．菱形 B．正方形 C．矩形 D．等腰梯形

第15题图 第16题 第17题图
16.如图,在△ABC中,∠C＝90°,DE的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为( )
A.45°－α2B.α2C.45°＋α2D.25°＋α2
17.把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则BC所对圆心角的度数是( )
A.120°B.135°C.150°D.165°
二、填空题
18.在同圆或等圆中，两个________、两条______、两条________中如果有一组量________，那么它们所对应的其余各组量都分别________，其依据是圆的____________性．
19.直径等于10 cm的圆内有长为5 cm的弦,则此弦所对的圆心角为 .
20.如图,在☉O中,AB为☉O的直径,E,F为BC的三等分点,∠BOF＝35°,则∠AOC＝ .

第20题图 第21题 第22题图
21.如图,有一块三角板ABO,∠B＝30°,直角顶点O与量角器的中心重合,AB与量角器交于点A,C.若量角器的半径为5 cm,则线段BC的长为 cm.
22.如图,C为AB的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= cm.
三、解答题
23.如图,已知OA,OB,OC是☉O的三条半径,AC和BC相等,M,N分别是OA,OB的中点.求证:MC＝NC.
24.如图,在☉O中,AC=BD,∠1=30°,求∠2的度数.
25.(中考·牡丹江)如图，在⊙O中，AC＝CB，CD⊥OA于点D，CE⊥OB于点E.求证：AD＝BE.
26.如图,已知AB是☉O的直径,弦AC∥OD.
(1)求证:BD＝CD;
(2)若AC所对圆心角的度数为58°,求∠AOD的度数.
27.如图,AB,AC是☉O的两条弦,且AB＝AC.
(1)求证:AO平分∠BAC;
(2)若S△ABC＝32,BC＝8,求半径OA的长.
28.如图，以▱ABCD的顶点A为圆心，AB为半径作圆，分别交AD，BC于点E，F，延长BA交⊙A于点G.
(1)求证：GE＝EF；
(2)若BF的度数为50°，求∠C的度数．
29.(2019·绵阳)如图，AB是⊙O的直径，点C为BD的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF.
(1)求证：△BFG≌△CDG；
(2)若AD＝BE＝2，求BF的长．
30.如图1,PC是☉O的直径,PA与PB是☉O的弦,且∠APC＝∠BPC.
(1)求证:PA＝PB.
(2)如图2,如果P为圆外一点,PC过圆心,是否仍有PA＝PB?为什么?
(3)如图3,如果P为圆内一点,PC过圆心,是否仍有PA＝PB?(直接写出结论,不必说明理由)
参考答案
一、选择题
1.下列语句中,不正确的是(C)
A.圆是中心对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.将圆绕它的中心旋转89°57',不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
2.下列图形中,∠AOB是圆心角的是(C)
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,则AC所对的圆心角的度数为(D)
A.60°B.75°C.80°D.90°

第3题图 第4题图 第5题图 第6题图
4.如图,A,B,C是☉O上的三点,AB,AC位于圆心O的两侧.若∠ABO＝20°,∠ACO＝30°,则∠BOC的度数为(A)
A.100°B.110°C.125°D.130°
5.如图,在☉O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB＝CD,则下列结论错误的是(C)
A.∠AON＝∠DOMB.AN＝DM
C.OM＝DMD.OM＝ON
6.如图,在☉O中,如果∠AOB＝2∠COD,那么(D)
A.AB＝DCB.AB2DCD.AB<2DC
7.如图,在☉O中,AC＝2AB,则下列数量关系正确的是(C)
A.AB＝ACB.AC＝2ABC.AC<2ABD.AC>2AB

第7题图 第8题图 第9题图 第10题图
8.如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC＝CD＝DA,则∠BCD等于(C)
A.100°B.110°C.120°D.135°
9.如图,在☉O中,如果∠AOB=2∠COD,那么( D )
A.AB=DCB.ABC.AB>2DCD.AB<2DC
10.如图，AB是⊙O的直径，点C，D在⊙O上，四边形ABCD中，BC＝CD＝DA＝4cm，则⊙O的周长为( D )
A.5π cmB.6π cmC.7π cmD.8π cm
11.如图，AB，CD分别为⊙O的两条弦，OM⊥AB于点M，ON⊥CD于点N，且∠AOB＝∠COD，则下列结论：
①AB＝CD；
②OM＝ON；
③AB＝CD.
其中正确的个数为( D )
A．0 B．1 C．2 D．3

第11题图 第12题 第13题图 第14题图
12.如图，在⊙O中，∠AOB＝2∠COD，则AB与2CD的大小关系是( )
A. AB＝2CD B. AB＞2CD
C. AB＜2CD D.不能确定
【答案】A
13.如图，在⊙O中，AB＝CD，则下列结论：
①AB＝CD；
②AC＝BD；
③∠AOC＝∠BOD；
④AC＝BD.
其中正确的个数是( D )
A．1 B．2 C．3 D．4
14.(中考·兰州)如图，在⊙O中，点C是AB的中点，∠A＝50°，则∠BOC等于( A )
A．40° B．45° C．50° D．60°
15.如图，△ABC的各顶点都在⊙O上，D，E，F是三边的中点，若AB＝AC，则四边形AEDF的形状是( A )
A．菱形 B．正方形 C．矩形 D．等腰梯形

第15题图 第16题 第17题图
16.如图,在△ABC中,∠C＝90°,DE的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为(A)
A.45°－α2B.α2C.45°＋α2D.25°＋α2
17.把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则BC所对圆心角的度数是(C)
A.120°B.135°C.150°D.165°
二、填空题
18.在同圆或等圆中，两个________、两条______、两条________中如果有一组量________，那么它们所对应的其余各组量都分别________，其依据是圆的____________性．
【答案】圆心角 弧 弦 相等 相等 旋转不变
19.直径等于10 cm的圆内有长为5 cm的弦,则此弦所对的圆心角为 60° .
20.如图,在☉O中,AB为☉O的直径,E,F为BC的三等分点,∠BOF＝35°,则∠AOC＝ 75° .

第20题图 第21题 第22题图
21.如图,有一块三角板ABO,∠B＝30°,直角顶点O与量角器的中心重合,AB与量角器交于点A,C.若量角器的半径为5 cm,则线段BC的长为 5 cm.
22.如图,C为AB的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= 2 cm.
三、解答题
23.如图,已知OA,OB,OC是☉O的三条半径,AC和BC相等,M,N分别是OA,OB的中点.求证:MC＝NC.
略
24.如图,在☉O中,AC=BD,∠1=30°,求∠2的度数.
解:∵在☉O中,AC=BD,∴∠AOC=∠BOD,
∴∠1+∠BOC=∠2+∠BOC,∴∠1=∠2=30°.
25.(中考·牡丹江)如图，在⊙O中，AC＝CB，CD⊥OA于点D，CE⊥OB于点E.求证：AD＝BE.
证明：连接OC.
∵AC＝CB，∴∠AOC＝∠BOC.
∵CD⊥OA于点D，CE⊥OB于点E，
∴∠CDO＝∠CEO＝90°.
在△COD和△COE中，
eq \b\lc\{(\a\vs4\al\c1(∠DOC＝∠EOC，,∠CDO＝∠CEO，,CO＝CO，))
∴△COD≌△COE(AAS)．
∴OD＝OE.
又∵AO＝BO，∴AD＝BE.
26.如图,已知AB是☉O的直径,弦AC∥OD.
(1)求证:BD＝CD;
(2)若AC所对圆心角的度数为58°,求∠AOD的度数
.
解:(1)连接OC.∵OA＝OC,∴∠OAC＝∠ACO.
∵AC∥OD,∴∠OAC＝∠BOD,∠COD＝∠ACO,
∴∠BOD＝∠COD,∴BD＝CD.
(2)∵BD＝CD,∠AOC＝58°,∴∠BOD＝∠COD＝12∠BOC＝12(180°－58°)＝61°,
∴∠AOD＝∠AOC＋∠COD＝119°.
27.如图,AB,AC是☉O的两条弦,且AB＝AC.
(1)求证:AO平分∠BAC;
(2)若S△ABC＝32,BC＝8,求半径OA的长.
解:(1)连接OB,OC.
∵AB＝AC,OB＝OC,OA＝OA,
∴△AOB≌△AOC(SSS),
∴∠BAO＝∠CAO,∴AO平分∠BAC.
(2)延长AO交BC于点E.
∵AB＝AC,AO平分∠BAC,
∴AE⊥BC,∴S△ABC＝12AE·BC,∴AE＝8.
连接OB,设OB＝x,
在Rt△OBE中,OB2＝BE2＋DE2,
且BE＝12BC＝4,OE＝8－x,
∴x2＝42＋(8－x)2,
解得x＝5,故半径OA的长为5.
28.如图，以▱ABCD的顶点A为圆心，AB为半径作圆，分别交AD，BC于点E，F，延长BA交⊙A于点G.
(1) 求证：GE＝EF；
证明：连接AF，则AB＝AF，
∴∠ABF＝∠AFB.
∵四边形ABCD是平行四边形，
∴AD∥BC.
∴∠EAF＝∠AFB，∠GAE＝∠ABF.
∴∠GAE＝∠EAF.
∴GE＝EF.
(2)若BF的度数为50°，求∠C的度数．
解：∵BF的度数为50°，
∴∠BAF＝50°.
∴∠ABF＝∠AFB＝65°.
∵AB∥CD，∴∠ABF＋∠C＝180°.
∴∠C＝180°－∠ABF＝115°.
29.(2019·绵阳)如图，AB是⊙O的直径，点C为BD的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF.
(1) 求证：△BFG≌△CDG；
证明：如图，连接BC.
∵C是BD的中点，∴CD＝BC.
∵AB是⊙O的直径，且CF⊥AB，
∴BC＝BF.
∴CD＝BF.
∴CD＝BF，BD＝CF.
∴BD＝CF.
在△BCD和△CBF中，
eq \b\lc\{(\a\vs4\al\c1(CD＝BF，,BD＝CF，,BC＝CB，))
∴△BCD≌△CBF(SSS)．
∴∠BDC＝∠F.
在△BFG和△CDG中，
eq \b\lc\{(\a\vs4\al\c1(∠F＝∠CDG，,∠FGB＝∠DGC，,BF＝CD，))
∴△BFG≌△CDG(AAS)．
(2) 若AD＝BE＝2，求BF的长．
【思路点拨】求BF的长，可以连接OC交BD于点H，根据垂径定理的推论和三角形的中位线定理可得OH＝1，证明△COE≌△BOH，并利用勾股定理可得结论．
解：如图，连接OC，交BD于点H.
∵C是BD的中点，
∴OC⊥BD，DH＝BH.
∵OA＝OB，∴OH＝eq \f(1,2)AD＝1.
∵OC＝OB，∠COE＝∠BOH，∠OHB＝∠OEC＝90°，
∴△COE≌△BOH(AAS)．
∴OE＝OH＝1.
∴OC＝OB＝OE＋BE＝1＋2＝3.
∴EF＝CE＝eq \r(32－12)＝2eq \r(2).
∴BF＝eq \r(BE2＋EF2)＝eq \r(22＋（2\r(2)）2)＝2eq \r(3).
30.如图1,PC是☉O的直径,PA与PB是☉O的弦,且∠APC＝∠BPC.
(1)求证:PA＝PB.
(2)如图2,如果P为圆外一点,PC过圆心,是否仍有PA＝PB?为什么?
(3)如图3,如果P为圆内一点,PC过圆心,是否仍有PA＝PB?(直接写出结论,不必说明理由)
解:(1)作OE⊥PA于点E,OF⊥PB于点F,
∴∠OEP＝∠OFP＝90°.
在△POE和△POF中,∠OEP＝∠OFP,∠APC＝∠BPC,OP＝OP,
∴△POE≌△POF(AAS),∴PE＝PF.
又∵PE＝12PA,PF＝12PB,∴PA＝PB.
(2)作OE⊥PA于点E,OF⊥PB于点F,
∴∠OEP＝∠OFP＝90°.
在△POE和△POF中,∠OEP＝∠OFP,∠APC＝∠BPC,OP＝OP,
∴△POE≌△POF(AAS),
∴OE＝OF,PE＝PF,
∴AE＝BF,∴PA＝PB.
(3)仍有PA＝PB.