人教版八年级上册第十一章 三角形综合与测试评课课件ppt

这是一份人教版八年级上册第十一章 三角形综合与测试评课课件ppt，共24页。PPT课件主要包含了三角形，与三角形有关的线段，三角形的内角和，三角形的外角和，知识梳理，三角形的三边关系，三角形的重心，三角形的稳定性，重难剖析，∠ADB等内容，欢迎下载使用。

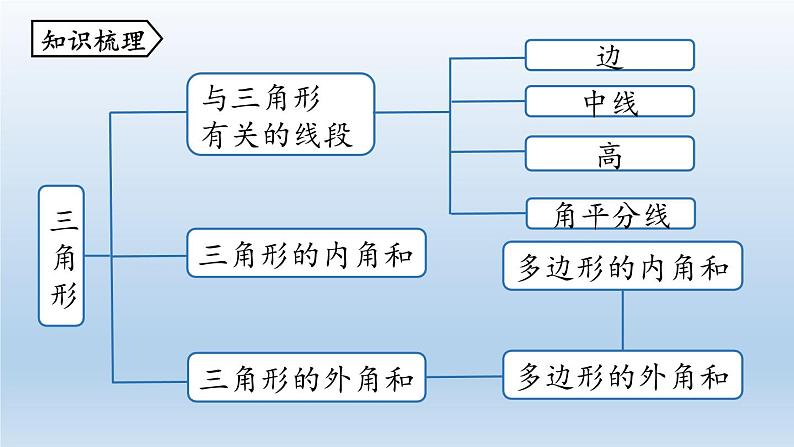
三角形两边之和大于第三边，三角形两边之差小于第三边.
2.三角形的高、中线、角平分线的定义
从三角形的一个顶点向它所对的边所在直线画垂线，顶点与垂足之间的线段叫做三角形的这条边上的高.连接三角形的一个顶点和它所对的边的中点，所得线段叫做三角形这条边上的中线.
三角形一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线.
三角形的三条中线的交点叫做三角形的重心.
三角形具有稳定性，四边形具有不稳定性.
1.下列各组线段能构成三角形的是（ ） A.3cm，3cm，7cm B.4cm，2cm，8cm C.1cm，1cm，2cm D.3cm，5cm，6cm
A.3+3<7，不能构成三角形.B.4+2<8，不能构成三角形.C.1+1=2，不能构成三角形.D.3+5>6，可以构成三角形.
根据“两条较短的线段之和大于第三条线段”判断即可.
解析：若5cm为腰，设另外一边为x cm. 则5+5+x=23，解得x=13. 此时5+5<13，不能构成三角形. 若5cm为底边，设另外一边为x cm. 则5+x+x=23，解得x=9. 此时5+9>9，可以构成三角形.
2.等腰三角形的周长为23cm，一边长5cm，则另外一边长为（ ）.
利用三角形的三边关系判断是否能构成三角形.
A.正方形 B.平行四边形 C.直角三角形 D.长方形
3.下列具有稳定性的是（ ）
4.在△ABC中，AD是中线，若△ABC的面积为16，则△ABD的面积为（ ）
三角形具有稳定性.三角形的中线将三角形分成面积相等的两个小三角形.
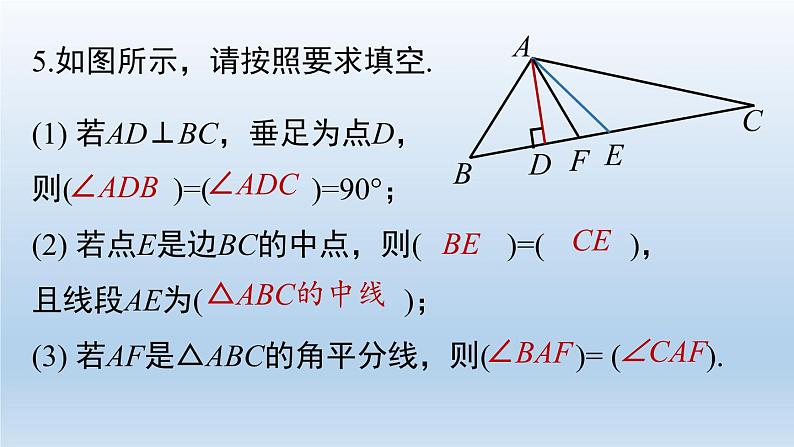
(1) 若AD⊥BC，垂足为点D，则( )=( )=90°；(2) 若点E是边BC的中点，则( )=( )，且线段AE为( )；(3) 若AF是△ABC的角平分线，则( )= ( ).
5.如图所示，请按照要求填空.
1.三角形的内角和定理
三角形三个内角的和等于180°.
直角三角形的两个锐角互余.有两个角互余的三角形是直角三角形.
3.三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
4.三角形外角和的性质
三角形的外角和等于360°.
1.已知△ABC中，∠B=2(∠A+∠C)，则∠B的度数是( ) A.60° B.100° C.120° D.140°
解：在△ABC中，∠A+∠B+∠C=180°. ∵∠B=2（∠A+∠C）， ∴∠A+2（∠A+∠C）+∠C=180°， 即 3（∠A+∠C）=180°. ∴∠A+∠C=60°，则∠B=120°.
2.在△ABC中，AB⊥BC，∠C的度数是70°，则∠A的度数是（ ）
解：∵AB⊥BC， ∴∠B=90°. ∴∠A+∠C=90°， ∵∠C=70°， ∴∠A=20°.
3.在△ABC中，∠A=70°，∠B=40°，则∠ACD的度数是（ ）
解：∵∠ACD是△ABC的外角， ∠A=70°，∠B=40°， ∴ ∠ACD=∠A+∠B=110°.
1.多边形和正多边形的定义
在平面内，由一些线段首尾顺次相接组成的封闭图 形叫做多边形.各个角都相等，各个边都相等的多边形叫做正多边形.
n边形的内角和等于(n-2)×180°.
多边形的外角和等于360°.
4.正多边形的每一个内角度数的表示
5.正多边形的每一个外角度数的表示
1.一个多边形的内角和是720°，则这个多边形的边数是（ ） A.4 B.5 C.6 D.7
解：设这个多边形的边数为n， 则(n-2)×180°= 720°， 解得n=6.
2. 正多边形的一个内角等于120°，则该多边形是正（ ）边形.
解析：∵正多边形的一个内角等于120°， ∴正多边形的一个外角等于60°， ∴边数为360°÷60°=6.
3. 已知过多边形的一个顶点可以作出325条对角线，则这个多边形的边数是（ ）.
解析：设这个多边形的边数为n. 根据题意，得n-3=325，解得n=328.
4.已知一个多边形的内角和是外角和的2倍，求这个多边形的边数.
解：设这个多边形的边数为n. ∵内角和是外角和的2倍， ∴（n-2）×180°=360°×2， 解得n=6， ∴这个多边形的边数为6.
解析：当底边为5cm，腰为2cm时， ∵2+2<5， ∴不能构成三角形； 当底边为2cm，腰为5cm时， ∵2+5>5， ∴能构成三角形. 周长为5+5+2=12（cm）.
1.等腰三角形的两边长分别为2cm，5cm，则它的周长为（ ） A.9cm B.12cm C.9cm或12cm D.10cm或12cm
解析：∵a，b，c为△ABC的三条边， ∴a+b>c，c-a0，c-a-b<0. ∴∣a+b-c∣+∣c-a-b∣=（a+b-c）+（-c+a+b） =2a+2b-2c.
2.已知a，b，c是△ABC的三条边，化简∣a+b-c∣+ ∣c-a-b∣的结果为（ ） A.2a+2b-2c B.2a+2b C.2c D.0
解：∵BD平分∠ABC，∠ABC=∠C=2∠A， ∴∠1=∠2=∠A. 设∠1=∠2 =∠A=x°，则∠ABC=∠C=2x°. ∵在△ABC中，∠A+∠ABC+∠C=180°, ∴x+2x+2x=180，解得x=36. ∴∠A=36° ，∠ABC=∠C=2∠A=72°.
3.如图，已知BD平分∠ABC交AC于点D，且∠ABC= ∠C= 2∠A，求△ABC各角的度数.
解：∵∠ABD和∠ACE是△ABC的外角， ∴∠ABD=∠A+∠ACB， ∠ACE=∠A+∠ABC. ∴∠ABD+∠ACE =∠A+∠ACB+∠A+∠ABC =180°+55° =235°.
4.∠ABD和∠ACE是△ABC的两个外角，若∠A=55°，求∠ABD和∠ACE的度数和.