人教版八年级数学上册 第十一章 三角形 小结与复习课件

这是一份人教版八年级数学上册 第十一章 三角形 小结与复习课件，共25页。PPT课件主要包含了三角形，与三角形有关的线段，角平分线，与三角形有关的角，内角与外角关系，三角形的分类，多边形，多边形的内外角和，外角和360°，对角线等内容，欢迎下载使用。

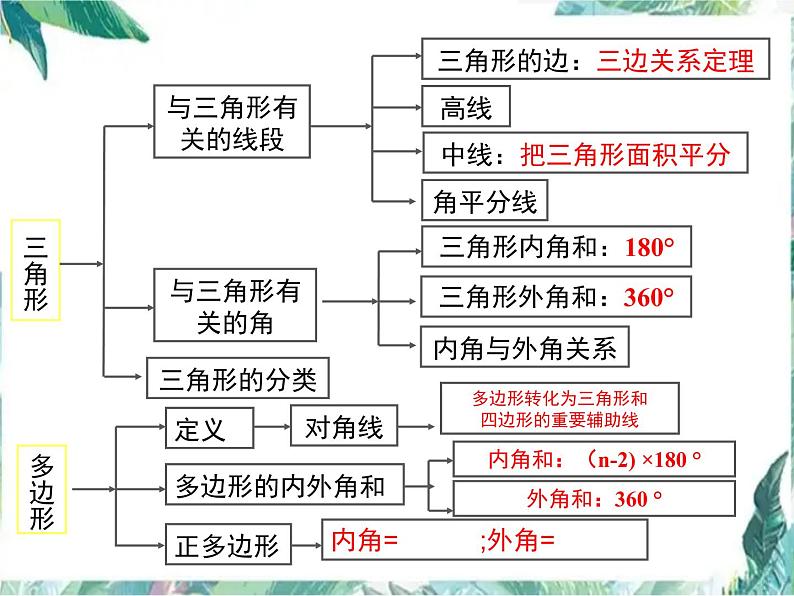
三角形内角和：180°
三角形外角和：360°
三角形的边：三边关系定理
中线：把三角形面积平分
内角和：（n-2) ×180 °
多边形转化为三角形和四边形的重要辅助线
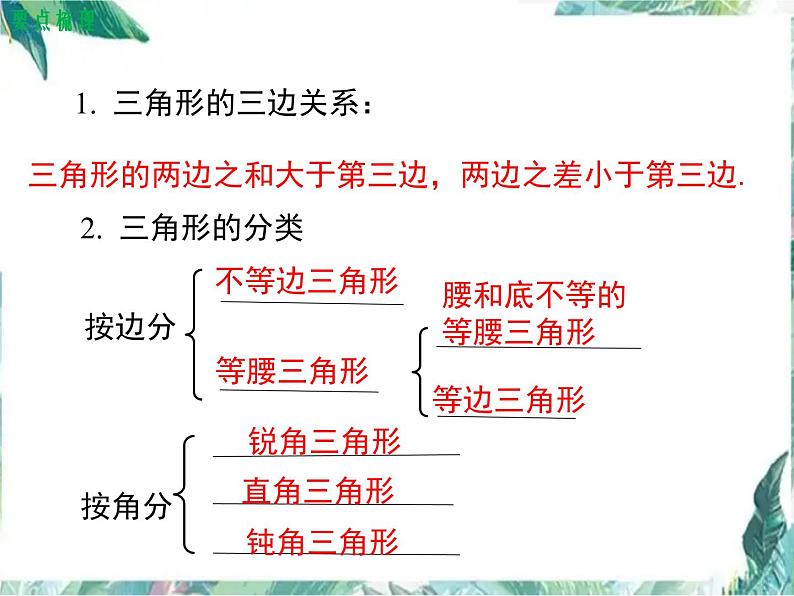
腰和底不等的等腰三角形
1. 三角形的三边关系：
三角形的两边之和大于第三边，两边之差小于第三边.
3. 三角形的高、中线与角平分线
高：顶点与对边垂足间的线段，三条高或其延长线 相交于一点，如图.中线：顶点与对边中点间的线段，三条中线相交于 一点（重心），如图.角平分线：三条角平分线相交于一点，如图.
4. 三角形的内角和与外角
(1)三角形的内角和等于180°；
(2)三角形的一个外角等于与它不相邻的两个内 角的和；(3)三角形的一个外角大于和它不相邻的任何一 个内角.
5. 多边形及其内角和
n边形内角和等于(n-2)×180 °(n ≥3的整数）.
n边形的外角和等于360°.
正多边形的每个内角的度数是
正多边形的每个外角的度数是
在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形.正多边形的各个角都相等，各条边都相等的多边形.
例1 有两根长度分别为5cm和8cm的木棒，用长度 为2cm的木棒与它们能摆成三角形吗？为什么？长 度为13cm的木棒呢？
解：取长度为2cm的木棒时，由于2+5=7<8，出现了两边之和小于第三边的情况，所以它们不能摆成三角形.取长度为13cm的木棒时，由于5+8=13，出现了两边之和等于第三边的情况，所以它们也不能摆成三角形.
例2 一个三角形的三边长分别为4，7，x，那么x的取值范围是(　　) A．3＜x＜11 B．4＜x＜7 C．－3＜x＜11 D．x＞3
解析：∵三角形的三边长分别为4，7，x，∴7－4＜x＜7＋4，即3＜x＜11.
例3 如图，D是△ABC 的边AC上一点，AD=BD，试判断AC 与BC 的大小.
有 BD+DC >BC（三角形的任意两边之和大于第三边）.
又因为 AD = BD，
则BD+DC = AD+DC = AC，
例4 作△ABC的边AB上的高，下列作法中，正确的是(　　)
例5 如图，已知AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，求∠ADB的度数．
解：∵AD是△ABC的角平分线，∠BAC＝60°， ∴∠DAC＝∠BAD＝30°.∵CE是△ABC的高，∠BCE＝40°，∴∠B＝50°，∴∠ADB＝180°－∠B－∠BAD＝180°－30°－50°＝100°.
【变式题】 在△ABC中，AB=AC，DB为△ABC的中线，且BD将△ABC周长分为12cm与15cm两部分，求三角形各边长．
解：如图，∵DB为△ABC的中线，∴AD=CD，设AD=CD=x，则AB=2x，当x+2x=12，解得x=4.BC+x=15，得BC=11.此时△ABC的三边长为AB=AC=8，BC=11；当x+2x=15，BC+x=12，解得x=5，BC=7，此时△ABC的三边长为AB=AC=10，BC=7．
例6 在△ABC中，AC＝5cm，AD是△ABC的中线，若△ABD的周长比△ADC的周长大2cm，则BA＝________.
提示：将△ABD与△ADC的周长之差转化为边长的差.
例7 如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
解：∵ＡE是△ABC的角平分线，
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°－∠B－∠C=180°－45°－60°=75°，∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C，∠CAE=∠BAE=37.5°，
∴∠AEB=37.5°+60°=97.5°.
例8 ∠A ,∠B ,∠C是△ABC的三个内角，且分别满足下列条件，求∠A，∠B，∠C中未知角的度数.(1)∠A－∠B＝16°，∠C＝54°；(2)∠A:∠B:∠C＝2:3:4.
解:(1)由∠C＝54°知∠A＋∠B＝180°－54°＝126°①,又∠A－∠B＝16°②,由①②解得∠A＝71°,∠B＝55°;
(2)设∠A＝2x，∠B＝3x，∠C=4x ， 则2x + 3x + 4x = 180° ，解得 x=20°， ∴∠A＝40°,∠B＝60°，∠C＝80°.
例9 如图，CD是∠ACB的平分线，DE∥BC，∠A＝50°，∠B＝70°，求∠EDC，∠BDC的度数．
解：∵∠A＝50°，∠B＝70°，∴∠ACB＝180°－∠A－∠B＝60°.∵CD是∠ACB的平分线，∴∠BCD＝ ∠ACB＝30°.∵DE∥BC，∴∠EDC＝∠BCD＝30°，在△BDC中，∠BDC＝180°－∠B－∠BCD=80°.
例10 如图，CE⊥AD，垂足为E，∠A=∠C，△ABD是直角三角形吗？为什么？
ABD是直角三角形.理由如下：∵CE⊥AD，∴∠CED=90°，∴∠C+∠D=90°，∵∠A=∠C，∴∠A+∠D=90°，∴△ABD是直角三角形.
例11 如图，∠A=51°，∠B=20°，∠C=30°，求∠BDC的度数.
解：连接AD并延长于点E.在△ABD中，∠1+∠ABD=∠3，在△ACD中，∠2+∠ACD=∠4.因为∠BDC=∠3+∠4，∠BAC=∠1+∠2，所以∠BDC=∠BAC+∠ABD+∠ACD =51° +20°+30°=101°.
解：设此多边形的外角的度数为x,则内角的度数为4x,则x+4x=180°,解得 x=36°.∴边数n=360°÷36°=10.
例13 如图，在四边形ABCD中，∠A与∠C互补，BE平分∠ABC，DF平分∠ADC，若BE∥DF，求证：△DCF为直角三角形．
证明：∵在四边形ABCD中，∠A与∠C互补，∴∠ABC+∠ADC=180°，∵BE平分∠ABC，DF平分∠ADC，∴∠CDF+∠EBF=90°，∵BE∥DF，∴∠EBF=∠CFD，∴∠CDF+∠CFD=90°，故△DCF为直角三角形．
例14 如图，在△ABC中， ∠C=∠ABC,BE⊥AC, △BDE是等边三角形，求∠C的度数.
解：设∠C=x °,则∠ABC=x°,因为△BDE是等边三角形，所以∠ABE=60°,所以∠ EBC=x°-60°.在△BCE中，根据三角形内角和定理，得90°+x°+x°-60°=180°,解得x=75,所以∠C=75 °.
例15 已知等腰三角形的两边长分别为10 和6 ，则三角形的周长是　　　　　．
【解析】 由于没有指明等腰三角形的腰和底，所以要分两种情况讨论：第一种10为腰，则6为底，此时周长为26；第二种10为底，则6为腰，此时周长为22.
例16 如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G的度数.
解析：所求问题不是常见的求多边形的内角和问题，我们发现，只要连接CD便转化为求五边形的内角和问题.
解：连接CD，由“8字型”模型图可知 ∠FCD+∠GDC=∠F+∠G,所以∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G=（5-2） ×180 °=540 °.