高中数学人教B版 (2019)必修 第三册8.2.3 倍角公式精品课件ppt

8.2.3 倍角公式

【学习重点】

二倍角公式与两角和与差的正弦余弦正切公式的区别与联系、二倍角公式及其变形公式的应用

【学习难点】

二倍角公式及其变形公式的应用

如若在两角和的正弦公式中，令，则可求出的公式，即

类似的，可得

因此：

这3个公式称为倍角公式。

需要注意的是，因为，所以也可以改写为：

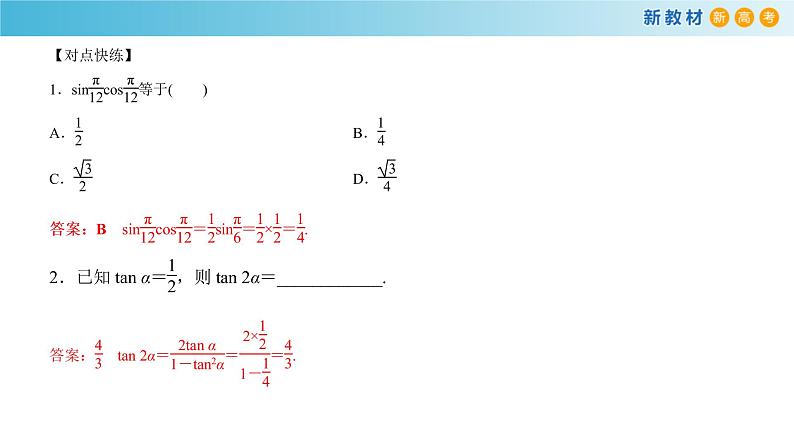
【对点快练】

1．sincos等于(　　)

A．　　　 B．　　　

C．　　　 D．

2．已知tan α＝，则tan 2α＝____________.

例1.已知 求的值。

【变式练习1】

求下列各式的值：

(1)coscos；(2)－cos2；(3)；

(4)sin 10°sin 50°sin 70°.

【变式练习2】

求下列各式的值．

(1)cos 72°cos 36°；(2)＋.

例2.已知sin＝，0<x<，求的值．

【变式练习】

已知sin α＋cos α＝(0＜α＜π)，则cos 2α＝____________.

例3.证明下列恒等式

【变式练习1】

求证：(1)cos2(A＋B)－sin2(A－B)＝cos 2Acos 2B；

(2)cos2θ(1－tan2θ)＝cos 2θ.

【变式练习2】

设α≠kπ＋，k∈Z，求证：tan＝.

例4.求函数的周期和最大值。

例5.已知函数 ，求的值域。

【变式练习1】

已知函数y＝cos2x＋sin xcos x＋1，x∈R.

(1)当函数y取得最大值时，求自变量x的集合；

【变式练习2】

已知不等式sincos ＋cos2－－m≥0对于x∈恒成立，则实数m的取值范围是(　　)

A．(－∞，－ ]　　　　 B．

C．　　 D．              

【变式练习3】

已知f(x)＝cos2＋sin xcos x．求：

(1)f(x)的最值；

(2)f(x)的对称轴方程．

例6.如图所示，已知中，为锐角，是边上的一点，且求的正弦值。