初中数学苏科版九年级上册2.2 圆的对称性教案配套ppt课件

这是一份初中数学苏科版九年级上册2.2 圆的对称性教案配套ppt课件，共26页。PPT课件主要包含了回顾与圆有关的概念，什么是中心对称图形，判断题，做做看你一定行，书P46，思考与讨论等内容，欢迎下载使用。

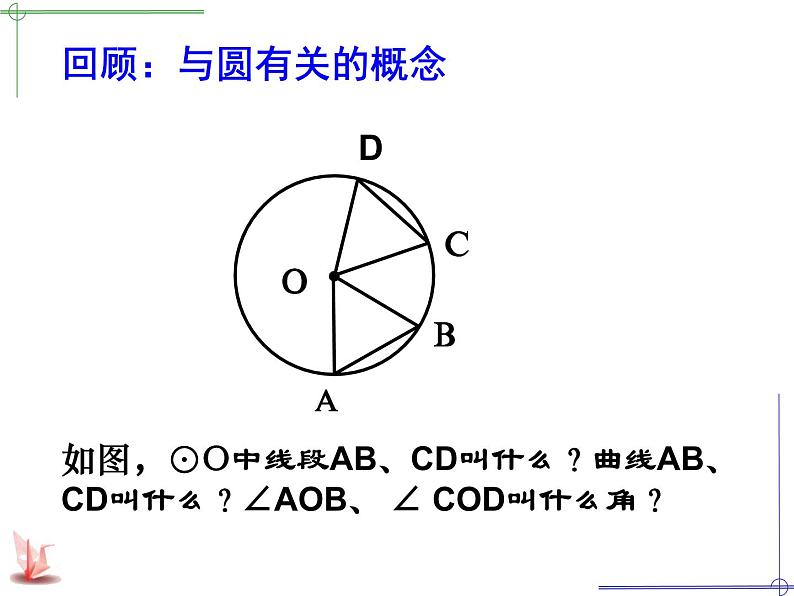
如图，⊙O中线段AB、CD叫什么？曲线AB、CD叫什么？∠AOB、 ∠ COD叫什么角？
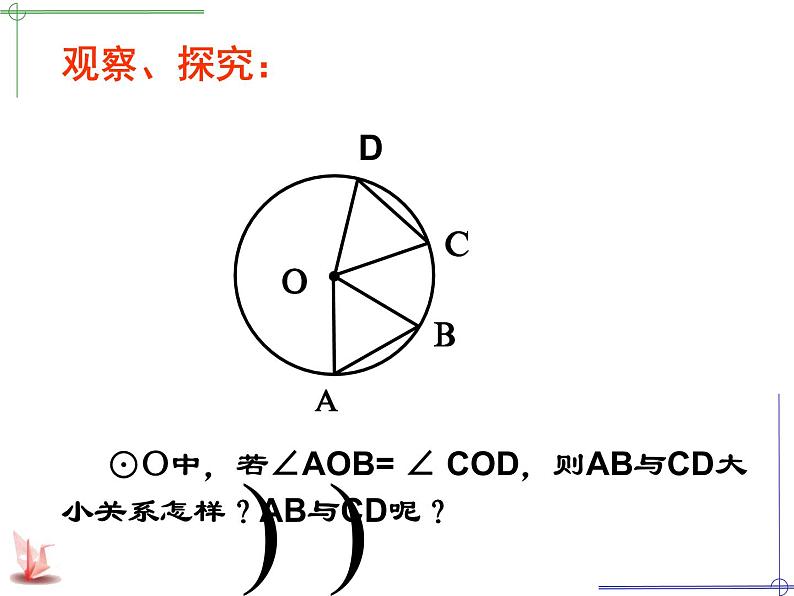
⊙O中，若∠AOB= ∠ COD，则AB与CD大小关系怎样？AB与CD呢？
把一个平面图形绕着某一点旋转180°，如果旋转后的图形能够和原图形互相重合，那么这个图形叫做中心对称图形.这个点就是它的对称中心.
圆是中心对称图形吗?它的对称中心是什么？
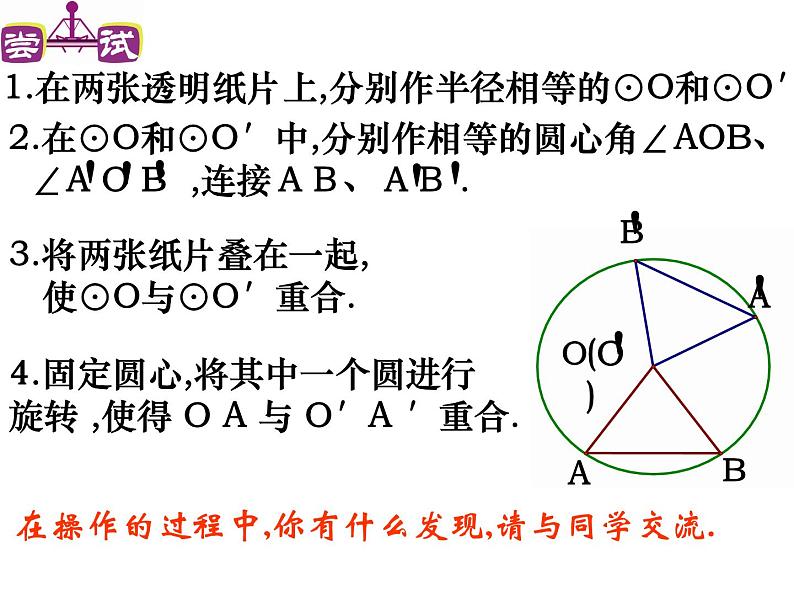
2.在⊙O和⊙O′中,分别作相等的圆心角∠AOB、 ∠A O B ,连接ＡＢ、ＡＢ .
3.将两张纸片叠在一起, 使⊙O与⊙O′重合.
1.在两张透明纸片上,分别作半径相等的⊙O和⊙O′
在操作的过程中,你有什么发现,请与同学交流.
4.固定圆心,将其中一个圆进行旋转 ,使得 O A 与 O′A ′重合.
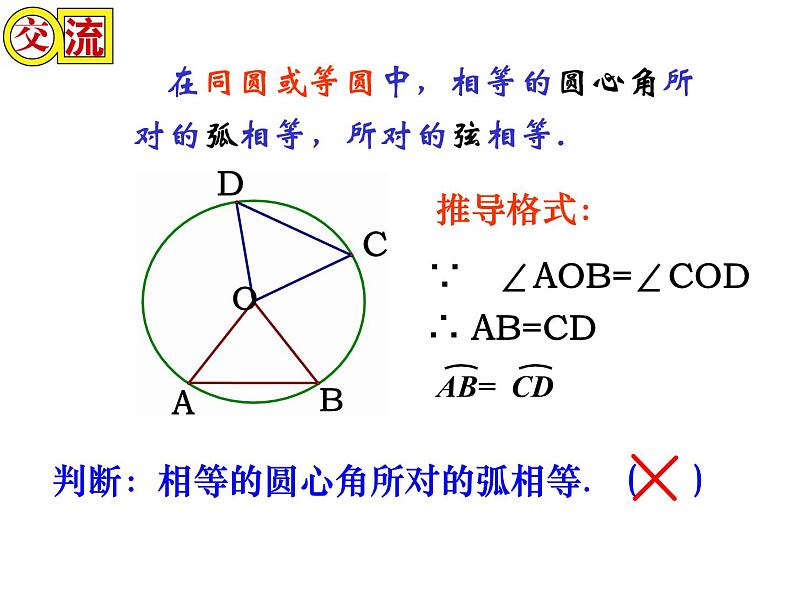
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.
判断：相等的圆心角所对的弧相等. ( )
∵　∠AOB=∠COD 　　
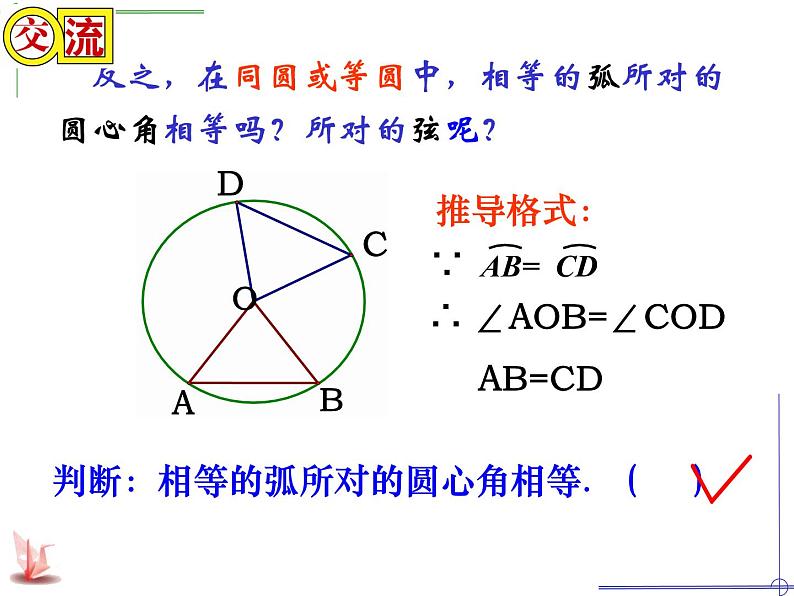
反之，在同圆或等圆中，相等的弧所对的圆心角相等吗？所对的弦呢？
判断：相等的弧所对的圆心角相等. ( )
∴ ∠AOB=∠COD
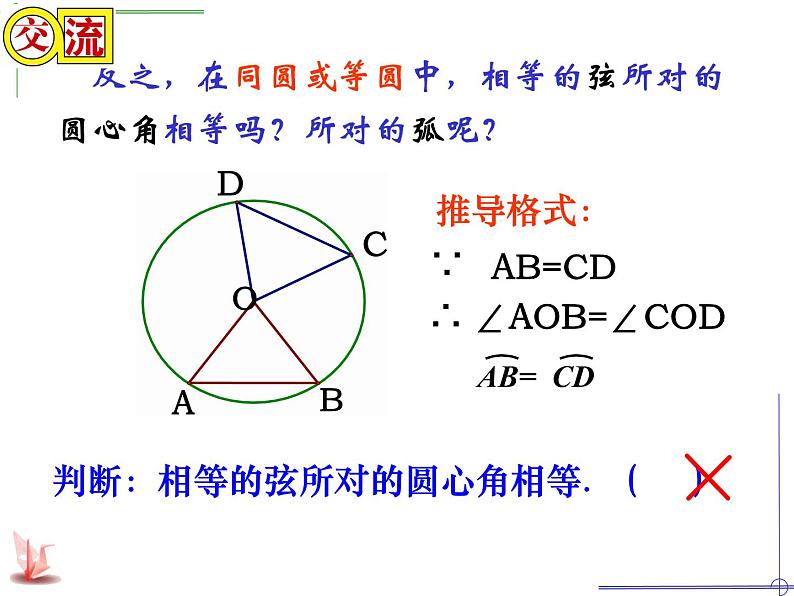
反之，在同圆或等圆中，相等的弦所对的圆心角相等吗？所对的弧呢？
判断：相等的弦所对的圆心角相等. ( )
在同圆或等圆中，如果两个圆心角、两条弧，两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等.
强调注意: 对应。如“弦所对的弧”是指“同为劣弧”要么 “同为优弧”
已知:如图,AB、AC、BC是⊙O的弦，∠AOC=∠BOC。 ∠ABC与∠BAC相等吗？为什么？
解：∠ABC与∠BAC相等
∵∠AOC=∠BOC 　　
∴ ∠ABC=∠BAC
已知:如图,弦AD=BC.求证:AB=CD
思路:欲证弦相等,只要证弦所对的弧相等, 或圆心角相等.
1.在圆心角、弧、弦这三个量中，角的大小可以用度数刻画，弦的大小可以用长度刻画，那么如何来刻画弧的大小呢？
将顶点在圆心的周角等分成360份,每一份的圆心角是10的角.这样整个圆也被等分成________份。
1°的圆心角所对的弧叫做1°的弧
2°的圆心角所对的弧就是2°的弧 ……
即n°的圆心角对着n°的弧, n°的弧对着n°的圆心角。
圆心角的度数和它所对的弧的度数相等.
则 的度数是 ____°
若 的度数是90°
则∠AOB=_____°
(3)长度相等的弧所对的圆心角相等 ( )
(1)相等的圆心角所对的弧相等。 （ ）
(2)相等的圆心角所对的弧的度数相等（ ）
等弧所对的圆心角相等 （ ）
2、下列命题中，真命题是（ ） A、若 和 的度数相等，那么 AB=CD； B、若⊙O中的弦AB和⊙O′中的弦CD的长度相等，则∠AOB=∠CO′D； C、⊙O中 的度数是 60°，⊙O′中 的度数是60°，则∠AOB=∠CO′D； D、若⊙O的圆心角∠AOB和⊙O′中的圆心角∠CO′D相等,则 = 。
如图,△ABC中，AB=AC，以C为圆心CB长为半径作⊙C交AB于D、交AC于E， 的度数为40°.求∠A的度数.
1.如图,在⊙O中, ∠AOB=50°,AC = BD , 求∠COD的度数．
2.如图,在⊙O中, ∠A=40°,AB = AC 求∠B的度数．
3.如图,在△ABC中, ∠C=90°, ∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC与点E,求AD、DE的度数.
4.如图,△ABC为等边三角形,以BC为直径 的⊙O交AB、AC于D、E. 求证:BD = DE = EC
5.如图,已知,AB是⊙O的直径,点C、D在⊙O上,CM⊥AB,DN⊥AB，且AM=BN.求证：AC = DB
3. 在同圆中,若 AB =2 CD , 则AB与2CD的大小关系是 （ 　） A． AB=2CD B．AB<2CD C． AB>2CD D．不能确定
已知:在⊙ O 中,若 AB = 3 CD那么,AB 与CD之间的关系为 ( )
已知:在⊙ O 中,若 AB = n CD (n为正整数)那么,AB 与CD之间的关系为 ( )
B、 AB ＜ nCD