





初中数学浙教版八年级上册第2章 特殊三角形2.4 等腰三角形的判定定理课文配套ppt课件
展开1.掌握等腰三角形的判定定理;2、能够区分等腰三角形的性质与判定方法,能综合利用等腰三角形的性质与判定进行简单的推理和计算;3、能应用等边三角形的性质和判定进行简单的推理和计算.
边:等腰三角形的两腰相等有两边相等的三角形是等腰三角形。角:等腰三角形的两个底角相等有两个角相等的三角形是等腰三角形。将上面两个命题的条件和结论互换,得到的新命题是真命题吗?
我们已经学习了等腰三角形的哪些性质?
如图所示,量出AC的长,就能算出河的宽度AB.你知道为什么吗?
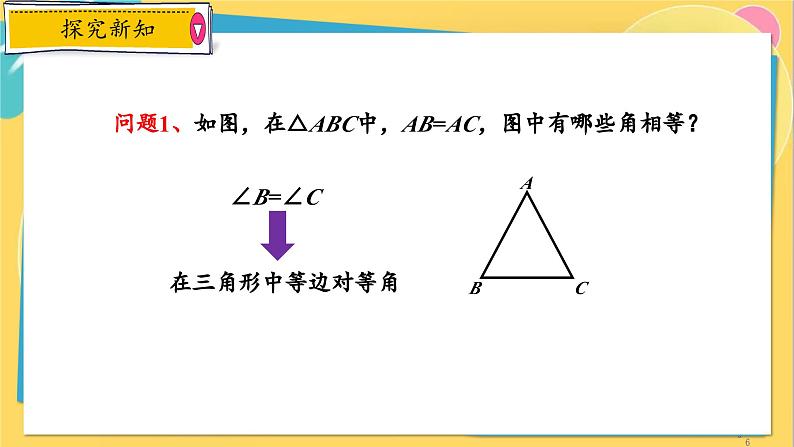
问题1、如图,在△ABC中,AB=AC,图中有哪些角相等?
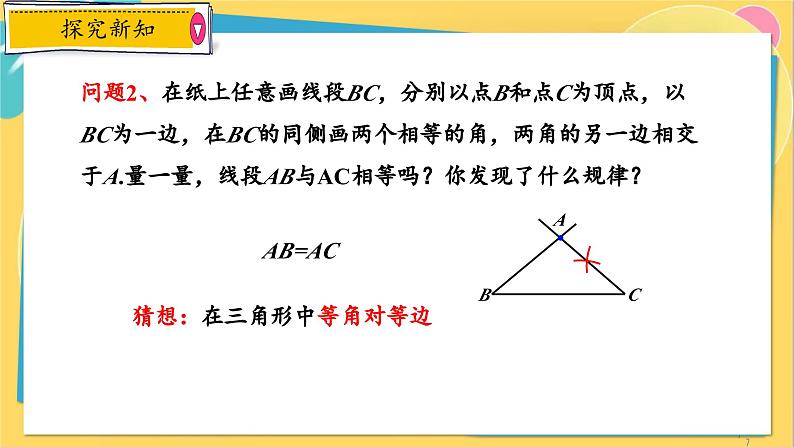
问题2、在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的另一边相交于A.量一量,线段AB与AC相等吗?你发现了什么规律?
猜想:在三角形中等角对等边
证明:作△ABC的角平分线AD.在△ABD和△ACD中,∵∠B=∠C,∠1=∠2,AD=AD,∴△ABD≌△ACD(AAS),∴AB=AC(全等三角形对应边相等).∴△ABC是等腰三角形(定义).
已知:△ABC中,∠B=∠C.求证:AB=AC.
如果一个三角形有两个角相等,那么这个三角形是等腰三角形,也可以简单地说成“在同一个三角形中,等角对等边”.
几何语言在△ABC中,∵∠B=∠C(已知),∴AC=AB(在同一个三角形中,等角对等边),即△ABC为等腰三角形.
这又是一个判定两条线段相等根据之一.
思考:如图,下列推理正确吗?
∵∠1=∠2∴ BD=DC(等角对等边)
∵∠1=∠2∴ DC=BC(等角对等边)
错,因为都不是在同一个三角形中.
1、一个三角形中,有两个角的度数分别为20°和80°,那么这个三角形是等腰三角形. ( )2、一个等腰三角形的底角只能小于90°且大于0°.( )3、两腰相等的三角形是等腰三角形. ( )
如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠1=_____,∠2=_____,图中的等腰三角形有____________________________.
【分析】在△ABC中,∵∠A=36°,∠C=72°,∴∠B=72°,又∵∠DBC=36°,∴∠1=36°,∴∠2=∠1+∠A=72°.
△ABC,△ABD,△BDC
一次数学实践活动的内容是测量河宽.如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗?请说明理由.
解:这一方法正确.理由如下:∵∠DAC=∠B+∠C(三角形外角的性质),∴ ∠B=∠DAC-∠C=60°- 30°= 30°,∴ ∠B= ∠C ,∴ AB= AC(在同一个三角形中,等角对等边).
上午8时,一条船从A处出发以15海里每小时的速度向正北航行,9时45分到达B处,从A、B望灯塔C,测得∠NAC=26°, ∠NBC=52°求从B处到灯塔C的距离.
解:∵∠NBC=∠A+∠C,∴∠C=52°-26°= 26°. ∴ ∠C=∠NAC,∴ BA=BC(在一个三角形中,等角对等边).∵AB=15×1.75=26.25,∴BC=26.25.答:B处到灯塔C的距离为26.25海里.
边:等边三角形的三条边都相等有三边相等的三角形是等边三角形。角:等边三角形的三个角都相等三个角都相等的三角形是等边三角形。有一个角是60°的等腰三角形是等边三角形。将上面两个命题的条件和结论互换,得到的新命题是真命题吗?
我们已经学习了等边三角形的哪些性质?
问题1、三个内角都等于60 °的三角形是等边三角形吗?
是等边三角形.理由如下:∵∠A=∠B=∠C=60 °,∴AB=AC=BC (为什么?),∴△ABC是等边三角形(定义).
问题2、有一个内角等于60 °的等腰三角形是等边三角形吗?
是等边三角形.理由如下:假若AB=AC.则∠B=∠C,当顶角∠A=60 °时,∠B=∠C=60 °,∴∠A=∠B=∠C=60 °,∴ △ABC是等边三角形.
当底角∠B=60°时,则∠C=60 °,此时∠A=180°—(60°+60°)=60°,∴ ∠A=∠B=∠C=60 °,∴ △ABC是等边三角形.
由此,你得出什么结论?
1、三个角都相等的三角形是等边三角形.2、有一个角等于60°的等腰三角形是等边三角形.
如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.证明:△ACE是等边三角形.
【分析】利用平行线的性质以及平角的定义求出△ACE的每一个内角都是60°.
在下图三角形的边上找出一点,使得该点与三角形的两顶点构成等腰三角形.
∴B BAD CDE AED CDE CDE C,∴BAD 2CDE
解:∵AB AC,∴B C. ∵AD AE,∴ADE AED.
∵AED CDE C,ADC CDE ADE
如图,AB=AC,D是BC上一点,AD=AE,∠BAD=40°,求∠CDE的度数。
通过以上的解答大家发现当哪个角的度数为定值时,∠CDE为定值.
把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形。你能办到吗?请画示意图说明剪法。
36° 36° 72°
1. [情境题 生活应用]如图是一个自带支架的平板保护壳及其 简易图,若∠ ACB =∠ ABC , AB =12 cm,则 AC 的长 为( B )
2. [2023·丽水]如图,在△ ABC 中, AC 的垂直平分线交 BC 于点 D ,交 AC 于点 E ,∠ B =∠ ADB . 若 AB =4,则 DC 的长是 .
3. [新考向·知识情境化 2023·江西]将含30°角的直角三角板 和直尺按如图所示的方式放置,已知∠α=60°,点 B , C 表示的刻度分别为1 cm,3 cm,则线段 AB 的长为 cm.
数学九年级上册2.4 概率的简单应用评课ppt课件: 这是一份数学九年级上册<a href="/sx/tb_c98809_t3/?tag_id=26" target="_blank">2.4 概率的简单应用评课ppt课件</a>,共19页。PPT课件主要包含了知识点,中奖预测,游戏公平性,解画树状图得,保险领域,其他实际应用等内容,欢迎下载使用。
浙教版九年级上册2.4 概率的简单应用授课ppt课件: 这是一份浙教版九年级上册2.4 概率的简单应用授课ppt课件,共12页。PPT课件主要包含了知识复习,什么叫概率,估计概率,知识引入,例题分析,课内练习,安全隐患,环保靠大家,有机垃圾箱,有害垃圾箱等内容,欢迎下载使用。
浙教版九年级上册第2章 简单事件的概率2.4 概率的简单应用课文配套ppt课件: 这是一份浙教版九年级上册第2章 简单事件的概率2.4 概率的简单应用课文配套ppt课件,共13页。













