浙教版八年级上册2.4 等腰三角形的判定定理完美版课件ppt

第2章  特殊三角形

2.4 等腰三角形的判定定理

1.探索等腰三角形判定定理,掌握反证法

2.理解等腰三角形的判定定理，并会运用其进行简单的证明.

3.培养学生的逆向思维能力.

理解等腰三角形的判定定理.

了解反证法的基本证明思路，并能简单应用.

问题1.等腰三角形性质定理的内容是什么？这个命题的题设和结论分别是什么？

问题2.我们是如何证明上述定理的？

【教学说明】通过问题回顾等腰三角形的性质定理以及证明的思路，要求学生独立思考后再进行交流.

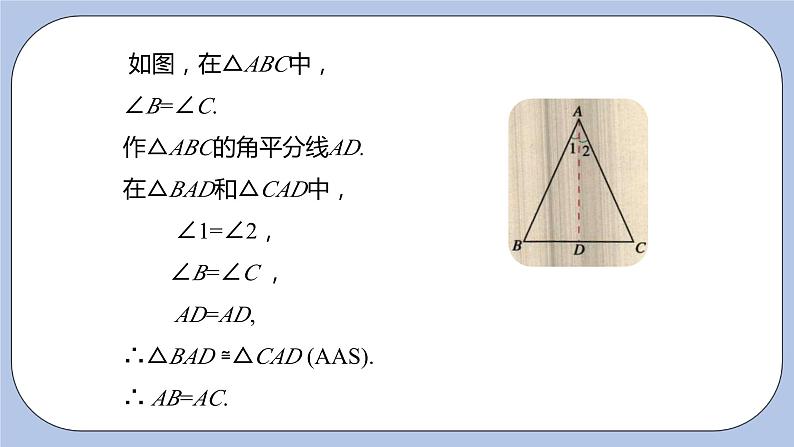
1.我们把等腰三角形的性质定理的条件和结论反过来还成立吗？如果一个三角形有两个角相等，那么这两个角所对的边也相等吗？

【归纳结论】有两个角相等的三角形是等腰三角形.（简称：等角对等边）

2.小明说，在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等．你认为这个结论成立吗?如果成立，你能证明它吗?

我们来看一位同学的想法：

如图，在△ABC中，已知∠B≠∠C，此时AB与AC要么相等，要么不相等．

假设AB=AC，那么根据“等边对等角”定理可得∠C=∠B，但已知条件是∠B≠∠C．“∠C=∠B”与已知条件“∠B≠∠C”相矛盾，因此AB≠AC

你能理解他的推理过程吗?

再例如，我们要证明△ABC中不可能有两个直角，也可以采用这位同学的证法，假设有两个角是直角，不妨设∠A=90°，∠B=90°，可得∠A+∠B=180°，但∠A+∠B+∠C=180°, “∠A+∠B=180°”与“∠A+∠B+∠C=180°”相矛盾，因此△ABC中不可能有两个直角．

引导学生思考：上面两道题的证法有什么共同的特点呢?

【归纳结论】都是先假设命题的结论不成立，然后由此推导出了与已知公理或已证明过的定理相矛盾，从而证明命题的结论一定成立．这也是证明命题的一种方法，我们把它叫做反证法．

【教学说明】总结这一证明方法，叙述并阐释反证法的含义，让学生了解.

例1.已知：如图，∠CAE是△ABC的外角，AD∥BC且∠1=∠2．求证：AB=AC．

证明：∵AD∥BC，

∴∠1=∠B(两直线平行，同位角相等)，

∠2=∠C(两直线平行，内错角相等)．

又∵∠1=∠2，∴∠B=∠C．

∴AB=AC(等角对等边)．

例2.如图，BD平分∠CBA，CD平分∠ACB，且MN∥BC，设AB=12，AC=18，求△AMN的周长.

解：∵BD平分∠CBA，CD平分∠ACB，

∴∠MBD=∠DBC,∠NCD=∠BCD.

∵MN∥BC,

∴∠MDB=∠DBC,∠NDC=∠BCD.

∴∠MDB=∠MBD,∠NDC=∠NCD.

∴MB=MD,NC=ND.

∴C△AMN=AM+AN+MN=AM+AN+MD+ND=AM+AN+MB+NC

=(AM+MB)+(AN+NC) =AB+AC=30.

例3.如图，在△ABC中，BD⊥AC于D，CE⊥AB于E，BD = CE.求证：△ABC是等腰三角形.

解：∵S△ABC=(AB·CE)=(AC·BD)且BD = CE，

∴AB=AC.

∴△ABC是等腰三角形.

例4.如图，在△ABC中，AB = AC，DE∥BC，求证：△ADE是等腰三角形.

证明：∵AB = AC，

∴∠B=∠C，

∵DE∥BC，

∴∠B=∠E，∠D=∠C.

∴∠D=∠E.

∴△ADE是等腰三角形.

例5.垂直于同一条直线的两条直线平行.

证明：假设a、b 不平行，那么a、b 相交

∵a⊥c，b⊥c 

∴∠1=900，∠2=900 

∴ ∠1+∠2=180°

而a、b相交，则∠1+∠2≠180°与∠1+∠2=180°相矛盾.

∴假设不成立.

即：垂直于同一条直线的两条直线平行

【教学说明】学生在独立思考的基础上再小组交流,培养学生应用知识解决问题的能力.

本节课应掌握：

等腰三角形性质的判定的区别和联系.