







- 5.3《 圆的面积》课件+教案+同步练习 课件 91 次下载
- 5.4《 环形的面积》课件+教案+同步练习 课件 81 次下载
- 5.6《 扇形的面积》课件+教案+同步练习 课件 82 次下载
- 5.7《 确定起跑线》课件+教案+同步练习 课件 70 次下载
- 6.1《 百分数的意义和读写》课件+教案+同步练习 课件 79 次下载
人教版六年级上册3 圆的面积试讲课ppt课件
展开1、结合具体情境认识与圆相关的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。 2、在解决实际问题的过程中,通过独立思考、合作探究、讨论交流等活动,培养学生分析问题和解决问题的能力。 3、结合例题渗透传统文化的教育,通过体验图形和生活的联系感受数学的价值,提升学习的兴趣。
教学重点: 掌握计算组合图形面积的方法,并能准确计算。教学难点:对组合图形进行分析。
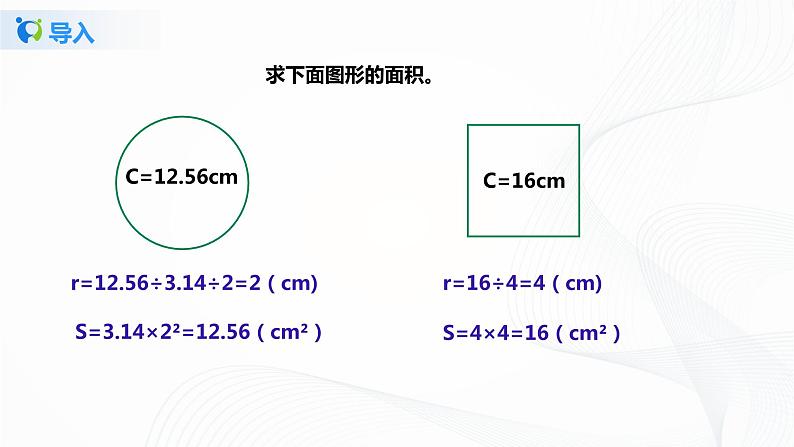
r=12.56÷3.14÷2=2(cm)
S=3.14×2²=12.56(cm²)
r=16÷4=4(cm)
S=4×4=16(cm²)
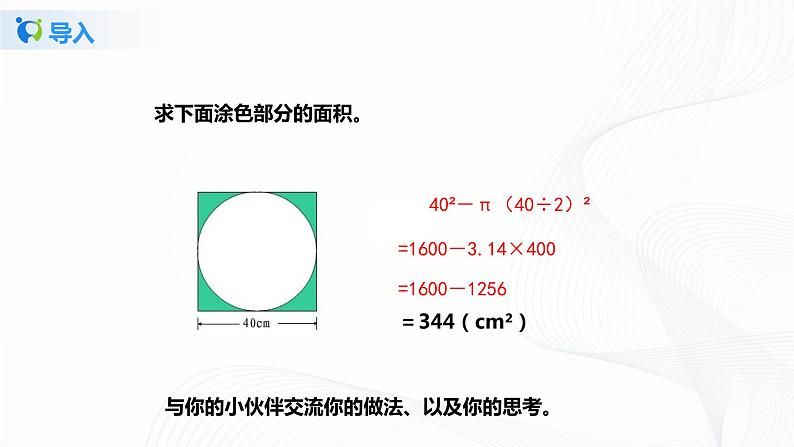
求下面涂色部分的面积。
40²-π(40÷2)²
=1600-3.14×400
与你的小伙伴交流你的做法、以及你的思考。
说说这两种设计有什么区别?
展示预习作业作品组合成的这两个图形。
怎样计算正方形和圆之间部分的面积?
这幅图求的是正方形的面积比圆的面积多多少。
正方形的面积-圆的面积
正方形的边长=圆的直径
2×2=4( m² ) 3.14×1²=3.14( m² ) 4-3.14=0.86( m² )
这幅图求的是圆的面积比正方形的面积多多少。
可以把正方形看成两个三角形。
3.14-2=1.14(m²)
( ×2×1)×2=2(m²)
如果两个圆的半径都是r,结果又是怎样的?
(2r)²-3.14×r²=4r²-3.14r²=0.86r²
3.14×r²- ( ×2r×r)×2=3.14r²-2r²=1.14r²
求下图中阴影部分的面积。
r=10÷2=5(cm) 4×5²-3.14×5²=21.5(cm²)
r=8÷2=4(cm) 3.14×4²-2×4²=18.24(cm²)
铜钱直径30mm,中间的正方形的边长是6mm。这个铜钱的面积是多少?
r=30÷2=15(cm) 3.14×15²-6×6=670.5(mm²)
答:这个铜钱的面积是670.5平方毫米。
下图是一个开关的盖子,已知正方形的边长是10厘米,和圆的半径之比是10:3。求盖子的面积是多少。
r= 10× =3(厘米)
10²-3.14×3²=100-28.26=71.74(平方厘米)
答:盖子的面积是多少71.74平方厘米。
求三角板的面积。
r= 4÷2=2(cm)
8×8÷2-3.14×2²=32-28.26=19.44(cm²)
答:三角板的面积是19.44平方厘米。
下面钢管的横截面积是多少?已知外圆的周长是18.84cm,正方形的边长是2厘米。
答:钢管的横截面积是24.26平方厘米。
18.84÷3.14÷2=3(cm)3.14×3²-2²=28.26-4=24.26(平方厘米)
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
周长:100×2+3.14×32×2
=200+200.96
答:这个运动场的周长是400.96m。
面积:100×(32×2)+3.14×322
=6400+3215.36
=9615.36(m2)
答:这个运动场的面积是9615.36m2。
1、在正方形ABCD中,AC=6厘米,求阴影部分的面积。
r²=6²=36(0.86×36)×=7.74(平方厘米)
可以认为是“外方内圆”的四分之一。
2、在下图中正方形的面积是30平方厘米,求阴影部分的面积。
可以认为是“外圆内方”的四分之一。
r²=30×4=120 1.14×120× =34.2(平方厘米)
外方内圆的面积=4r²-3.14r²=0.86r²
外圆内方的面积=3.14r²-2r²=1.14r²
课本第72页练习十五 10~17题
人教版六年级上册3 圆的面积教学演示ppt课件: 这是一份人教版六年级上册3 圆的面积教学演示ppt课件,共60页。PPT课件主要包含了八等分,十六等分,三十二等分,分的份数越多,基本练习等内容,欢迎下载使用。
小学数学人教版六年级上册3 圆的面积完美版ppt课件: 这是一份小学数学人教版六年级上册3 圆的面积完美版ppt课件,共19页。PPT课件主要包含了学习目标,课堂导入,你认识下面的物品吗,新知探究,πR2,πr2,圆环具有哪些特点,教材第72页例2,方法一,=314×32等内容,欢迎下载使用。
人教版六年级上册3 圆的面积作业ppt课件: 这是一份人教版六年级上册3 圆的面积作业ppt课件,共9页。















