初中数学浙教版八年级上册2.7 探索勾股定理课时作业

这是一份初中数学浙教版八年级上册2.7 探索勾股定理课时作业，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1.在下列以线段a、b、c的长为边，能构成直角三角形的是( ）
A．a=3，b=4，c=6 B．a=5，b=6，c=7 C．a=6，b=8，c=9 D．a=7，b=24，c=25
2.满足下列条件的三角形中，不是直角三角形的是( ）
A．三内角之比为1：2：3 B．三边长的平方之比为1：2：3
C．三边长之比为3：4：5 D．三内角之比为3：4：5
3.若△ABC的三边分别为5、12、13，则△ABC的面积是( )
A.30 B.40 C.50 D.60
4.三角形的三边长ａ,ｂ,ｃ满足2ab=(ａ+ｂ)2－ｃ2,则此三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等边三角形
5.如图，有一个由传感器控制的灯A装在门上方离地高4.5 m的墙上，任何东西只要移至距该灯5 m及5 m以内时，灯就会自动发光，请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光？( )
A．4 m B．3 m C．5 m D．7 m
6.如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度为(滑轮上方的部分忽略不计)( )
A．12 m B．13 m C．16 m D．17 m
7.国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营，西安至成都列车运行时间由14小时缩短为3.5小时．张明和王强相约从成都坐高铁到西安旅游．如图，张明家（记作A）在成都东站（记作B）南偏西30°的方向且相距4000米，王强家（记作C）在成都东站南偏东60°的方向且相距3000米，则张明家与王强家的距离为（ ）
A．6000米 B．5000米 C．4000米 D．2000米
8.将一根长24 cm的筷子，置于底面直径为5cm、高为12cm的圆柱形水杯中，设筷子露在杯子外面的长为hcm，则h的取值范围是（ ）
A．5≤h≤12 B．5≤h≤24 C．11≤h≤12 D．12≤h≤24
二、填空题
9.直角三角形的两边长为5和7，则第三边长为 .
10.如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为 ．
11.若三角形三边之比为3：4：5，周长为24，则三角形面积 ．
12.直角三角形的两直角边的长分别为6cm、8cm，则斜边上高的长是 cm．
13.以直角三角形一边向外作正方形，其中两个正方形的面积为100和64，则第三个正方形的面积为 ．
14.在△ABC和△DEC中，∠ACB=∠ECD=90°，AC=BC=12，DC=EC=5．当点A、C、D在同一条直线上时，AF的长度为 .
三、解答题
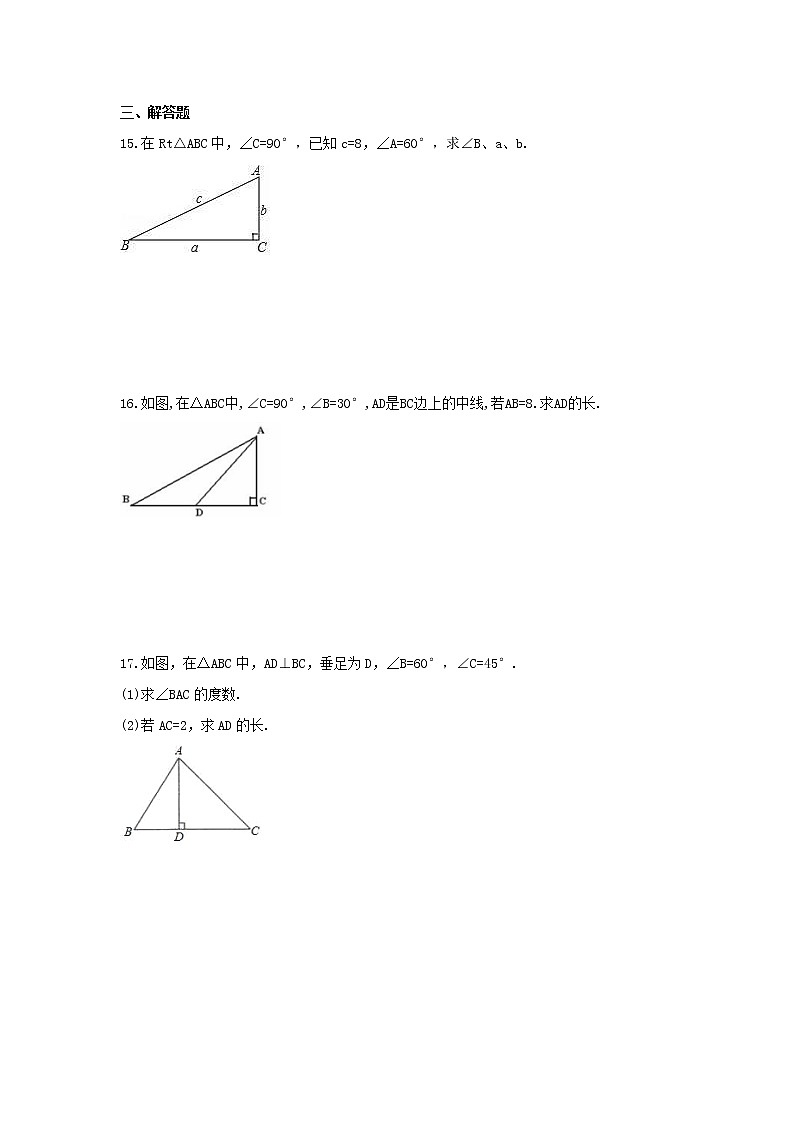
15.在Rt△ABC中，∠C=90°，已知c=8，∠A=60°，求∠B、a、b.
16.如图,在△ABC中,∠C=90°,∠B=30°,AD是BC边上的中线,若AB=8.求AD的长.

17.如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°.
(1)求∠BAC的度数.
(2)若AC=2，求AD的长.
18.正方形网格（边长为1的小正方形组成的网格纸，正方形的顶点称为格点）是我们在初中阶段常用的工具，利用它可以解决很多问题.
（1）如图①中，△ABC是格点三角形（三个顶点为格点），则它的面积为 ；
（2）如图②，在4×4网格中作出以A为顶点，且面积最大的格点正方形（四个顶点均为格点）；
（3）人们发现，记格点多边形（顶点均为格点）内的格点数为a，边界上的格点数为b，
则格点多边形的面积可表示为S=ma＋nb－1，其中m，n为常数.试确定m，n的值.
参考答案
1.答案为：D.
2.答案为：D.
3.答案为：A
4.答案为：C
5.答案为：A.
6.答案为：D.
7.答案为：B.
8.答案为：C；
9.答案为：2或
10.答案为14．
11.答案为：24；
12.答案为：4.8．
13.答案为：36或164．
14.答案为：
15.解：∵Rt△ABC中，∠C=90°，∠A=60°，
∴∠B=90°﹣∠A=30°，∴，
Rt△ABC中，∵a2+b2=c2，∴.
16.解：∵∠C=90°，∠B=30° ∴
在Rt△ABC中，

∵AD是BC边上的中线，
∴
在Rt△ACD中，
答：AD的长是。
17.解：(1)∠BAC=180°﹣60°﹣45°=75°；
(2)∵AD⊥BC，
∴△ADC是直角三角形，
∵∠C=45°，
∴∠DAC=45°，
∴AD=DC，
∵AC=2，
∴AD=.
18.解：（1）5；（2）画图略；（3）4m+4n-1=5,9m+4n-1=10.m=1,n=0.5.