高中数学人教版新课标A必修11.3.2奇偶性评课课件ppt

这是一份高中数学人教版新课标A必修11.3.2奇偶性评课课件ppt，共30页。PPT课件主要包含了探究一，探究二，探究三，思想方法，当堂检测，2图象法等内容，欢迎下载使用。
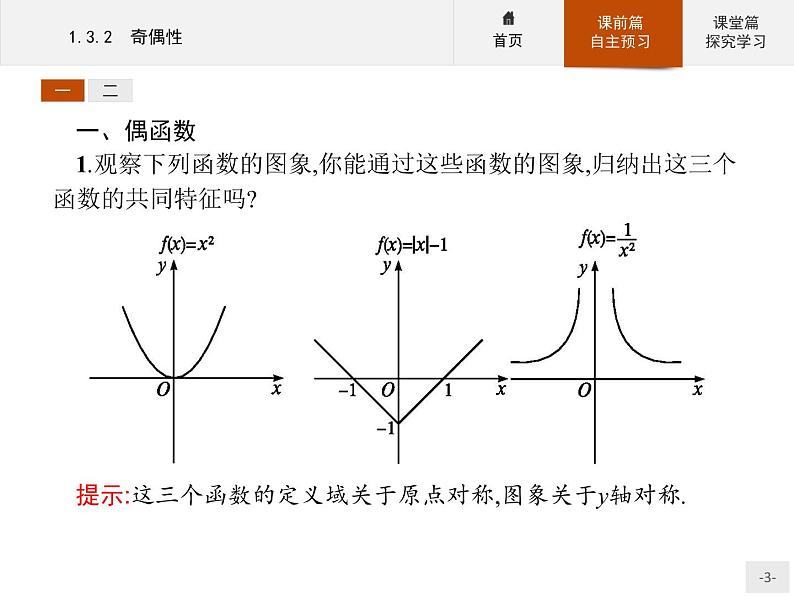
一、偶函数1.观察下列函数的图象,你能通过这些函数的图象,归纳出这三个函数的共同特征吗?
提示:这三个函数的定义域关于原点对称,图象关于y轴对称.
2.对于上述三个函数,f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系?这说明关于y轴对称的点的坐标有什么关系?提示:f(1)=f(-1),f(2)=f(-2),f(3)=f(-3).关于y轴对称的点的横坐标互为相反数,纵坐标相等.3.一般地,若函数y=f(x)的图象关于y轴对称,则f(x)与f(-x)有什么关系?反之成立吗?提示:若函数y=f(x)的图象关于y轴对称,则f(x)=f(-x).反之,若f(x)=f(-x),则函数y=f(x)的图象关于y轴对称.4.填空:(1)定义:对于函数f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)叫做偶函数.(2)偶函数的图象特征:图象关于y轴对称.
5.判断正误:定义在R上的函数f(x),若f(-1)=f(1),f(-2)=f(2),则f(x)一定是偶函数. (　　)答案:×6.做一做:下列函数中,是偶函数的是(　　)A.f(x)=x2B.f(x)=xC.f(x)=D.f(x)=x+x3答案:A
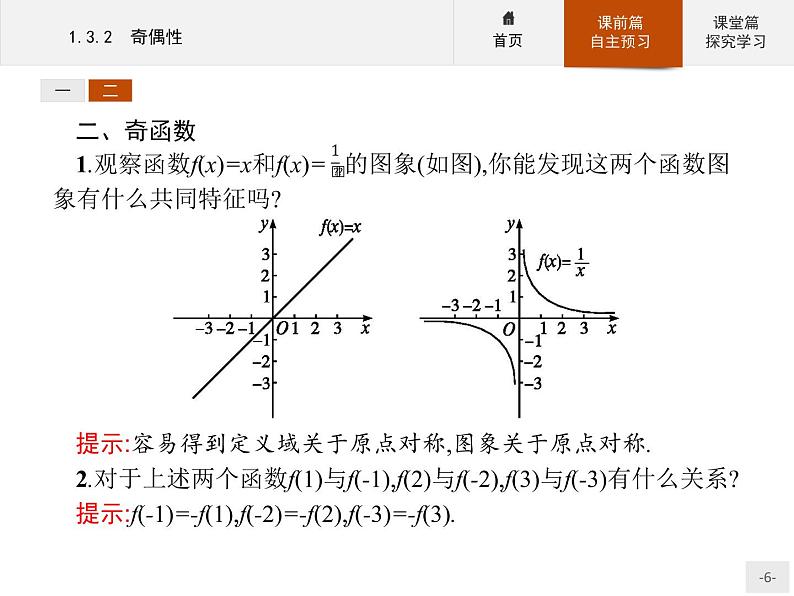
二、奇函数1.观察函数f(x)=x和f(x)= 的图象(如图),你能发现这两个函数图象有什么共同特征吗?提示:容易得到定义域关于原点对称,图象关于原点对称.2.对于上述两个函数f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系?提示:f(-1)=-f(1),f(-2)=-f(2),f(-3)=-f(3).
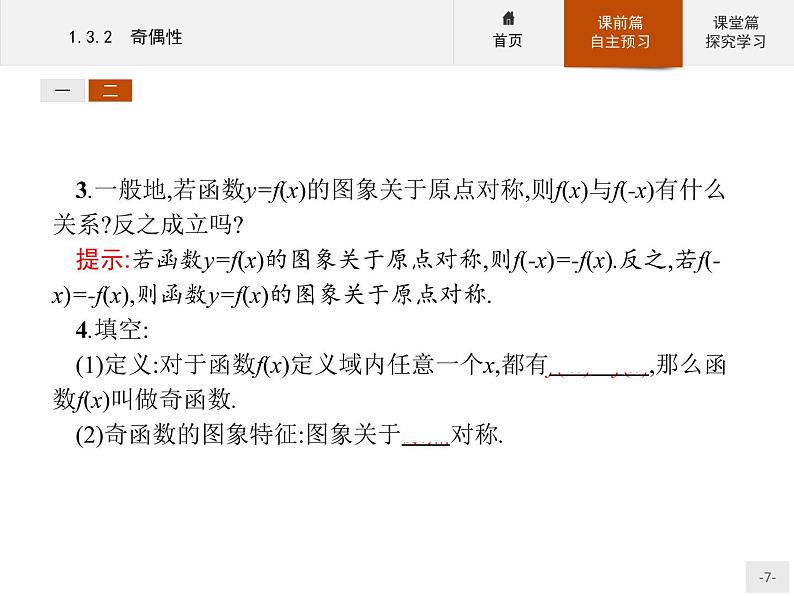
3.一般地,若函数y=f(x)的图象关于原点对称,则f(x)与f(-x)有什么关系?反之成立吗?提示:若函数y=f(x)的图象关于原点对称,则f(-x)=-f(x).反之,若f(-x)=-f(x),则函数y=f(x)的图象关于原点对称.4.填空:(1)定义:对于函数f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)叫做奇函数.(2)奇函数的图象特征:图象关于原点对称.
5.判断正误:(1)若f(x)是奇函数,则f(0)=0.(　　)(2)不存在既是奇函数又是偶函数的函数.(　　)答案:(1)×　(2)×
6.做一做:(1)函数f(x)= -x的图象关于(　　)对称.A.y轴B.直线y=-xC.坐标原点D.直线y=x(2)下列图象表示的函数具有奇偶性的是(　　)
解析:(1)因为f(x)= -x是奇函数,所以该函数的图象关于坐标原点对称.(2)选项A中的函数图象关于原点或y轴均不对称,故排除;选项C,D中的图象所表示函数的定义域不关于原点对称,不具有奇偶性,故排除;选项B中的图象关于y轴对称,其表示的函数是偶函数.故选B.答案:(1)C　(2)B
探究一判断函数的奇偶性例1判断下列函数的奇偶性:
分析:利用奇函数、偶函数的定义判断函数的奇偶性时,先求出函数的定义域,看其是否关于原点对称,如果定义域关于原点对称,再判断f(-x)与f(x)的关系.为了判断f(-x)与f(x)的关系,既可以从f(-x)开始化简整理,也可以考虑f(-x)+f(x)或f(-x)-f(x)是否等于0.当f(x)不等于0时也可考虑 与1或-1的关系,还可以考虑使用图象法.
解:(1)∵函数的定义域为{x|x≠-1},不关于原点对称,∴f(x)既不是奇函数又不是偶函数.(2)函数的定义域为R,关于原点对称,f(-x)=(-x)3-2(-x)=2x-x3=-f(x),∴f(x)是奇函数.
∴函数的定义域为{-1,1},关于原点对称.又f(1)=f(-1)=0,∴f(x)既是奇函数又是偶函数.
(4)函数的定义域关于原点对称.(方法一)当x>0时,-x0时,f(x)=-2x2+3x+1,(1)求f(-1);(2)求f(x)的解析式.分析:(1)根据奇函数的性质,将f(-1)转化为f(1)求解;(2)先设出所求区间上的自变量,利用奇函数、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,再次利用函数的奇偶性求解即可.注意不要忽略x=0时f(x)的解析式.
解:(1)因为函数f(x)为奇函数,所以f(-1)=-f(1)=-(-2×12+3×1+1)=-2.(2)当x0,则f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.由于f(x)是奇函数,则f(x)=-f(-x),所以f(x)=2x2+3x-1.当x=0时,f(-0)=-f(0),则f(0)=-f(0),即f(0)=0.
反思感悟1.这类问题常见的情形是:已知当x∈(a,b)时,f(x)=φ(x),求当x∈(-b,-a)时f(x)的解析式.若f(x)为奇函数,则当x∈(-b,-a)时,f(x)=-f(-x)=-φ(-x);若f(x)为偶函数,则当x∈(-b,-a)时,f(x)=f(-x)=φ(-x).2.若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,不能漏掉.
延伸探究若将本例中的“奇”改为“偶”,“x>0”改为“x≥0”,其他条件不变,求f(x)的解析式.
解:当x0,此时f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.由于f(x)是偶函数,则f(x)=f(-x)=-2x2-3x+1,
探究三分段函数的奇偶性问题解析:∵当x0,f(-x)=-(-x)2+2(-x)=-x2-2x,又f(x)为奇函数,∴f(-x)=-f(x)=-x2-2x.∴f(x)=x2+2x=x2+mx.∴m=2.答案:2反思感悟 分段函数奇偶性的判断技巧(1)分段函数的奇偶性应分段说明f(-x)与f(x)的关系,只有当对称区间上的对应关系满足同样的关系时,才能判断函数的奇偶性,否则该分段函数既不是奇函数也不是偶函数;(2)若能画出分段函数的图象,则利用图象的对称性去判断分段函数的奇偶性,这是一种非常有效的方法.
变式训练 2判断f(x)=|x+a|-|x-a|(a∈R)的奇偶性.分析:对a进行分类讨论.解:若a=0,则f(x)=|x|-|x|=0.因为x∈R,定义域R关于原点对称,所以f(x)既是奇函数,又是偶函数.当a≠0时,f(-x)=|-x+a|-|-x-a|=|x-a|-|x+a|=-(|x+a|-|x-a|)=-f(x),故f(x)是奇函数.综上,当a=0时,函数f(x)既是奇函数,又是偶函数;当a≠0时,函数f(x)是奇函数.
利用定义法、赋值法解决抽象函数奇偶性问题典例 若定义在R上的函数f(x)满足:对任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2),且当x>0时,f(x)