人教版新课标A必修11.3.2奇偶性图片ppt课件

这是一份人教版新课标A必修11.3.2奇偶性图片ppt课件，共47页。PPT课件主要包含了－fx，奇偶性，函数奇偶性的判断等内容，欢迎下载使用。

大自然是一个真正的设计师，它用对称的方法创造了千百万种不同的生命．被誉为“上海之鸟”的浦东国际机场的设计模型，是一只硕大无比、展开双翅的海鸥．它的两翼呈对称状，看上去舒展优美，它象征着浦东将展翅高飞，飞向更高、更广阔的天地，创造更新、更宏伟的业绩．一些函数的图象也有着如此美妙的对称性，那么这种对称性体现了函数的什么性质呢？
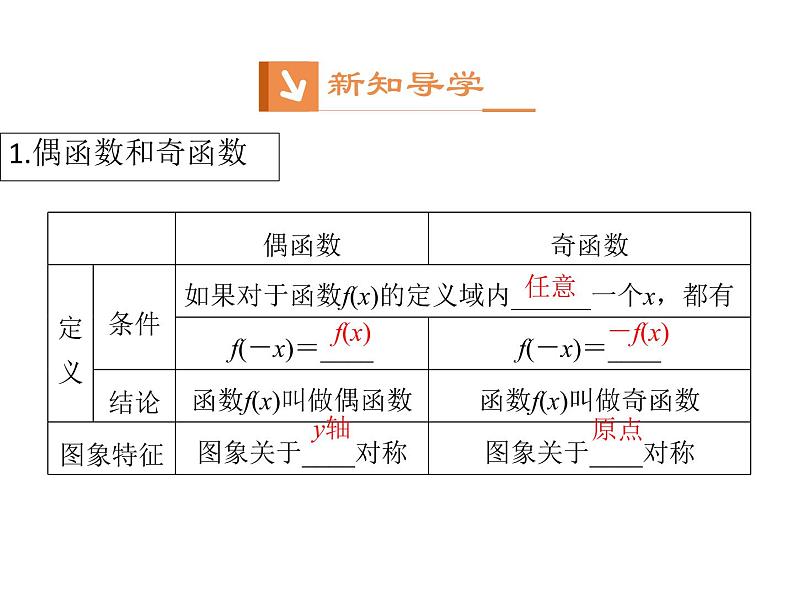
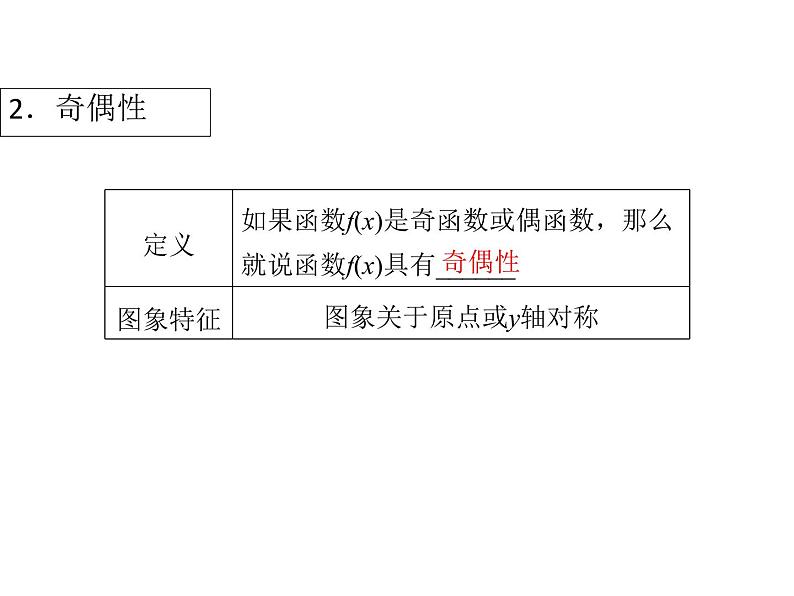
[知识点拨]　(1)奇函数和偶函数的定义中的“任意”是指定义域中所有的实数；由于f(－x)与f(x)有意义，则－x与x同时属于定义域，即具有奇偶性的函数的定义域关于原点对称．(2)函数f(x)是偶函数⇔对定义域内任意一个x，都有f(－x)－f(x)＝0⇔f(x)的图象关于y轴对称．(3)函数f(x)是奇函数⇔对定义域内任意一个x，都有f(－x)＋f(x)＝0⇔f(x)的图象关于原点对称．
[归纳总结]　基本初等函数的奇偶性如下：
[答案]　C[解析]　∵定义域为(0,1)不关于原点对称，∴函数为非奇非偶的函数，故选C.
[答案]　B[解析]　f(x)＝x－3是奇函数，A错误；f(x)＝x－4是偶函数且在(0，＋∞)上是减函数，B正确；f(x)＝x4是偶函数且在(0，＋∞)上增函数，C错误；f(x)＝x2是偶函数且在(0，＋∞)上是增函数，D错误．
[答案]　0[解析]　f(x)为偶函数，则对称轴为x＝m＝0.
[答案]　8[解析]　∵f(x)为[3－a,5]上的奇函数，∴区间[3－a,5]关于坐标原点对称，∴3－a＝－5，即a＝8.
[思路分析]　(1)函数具备奇偶性时，函数的定义域有什么特点？(2)判断函数的奇偶性应把握好哪几个关键点？
[分析]　根据函数奇偶性的定义，先看函数的定义域是否关于原点对称，若是，再检查函数解析式是否满足奇偶性的条件．
奇、偶函数图象的应用
[思路分析]　先利用函数的解析式得到函数f(x)的性质：f(－x)＝f(x)，根据函数图象关于y轴对称作出f(x)的图象．
[规律总结]　1.研究函数图象时，要注意对函数性质的研究，这样可避免作图的盲目性和复杂性．2．利用函数的奇偶性作图，其依据是奇函数图象关于原点对称，偶函数图象关于y轴对称．
利用函数的奇偶性求解析式
[规律总结]　利用函数奇偶性求函数解析式利用函数奇偶性求函数解析式的关键是利用奇偶函数的关系式f(－x)＝－f(x)或f(－x)＝f(x)成立，但要注意求给定哪个区间的解析式就设这个区间上的变量为x，然后把x转化为－x(另一个已知区间上的解析式中的变量)，通过适当推导，求得所求区间上的解析式．
[答案]　－x＋1[解析]　x>0时，－x<0，∴f(－x)＝－x＋1，又∵f(x)为偶函数，∴f(x)＝－x＋1.
利用函数奇偶性求值或参数
(2)因为f(x)是奇函数，所以f(－x)＝－f(x)，所以f(－2)＝－f(2)，f(－1)＝－f(1)，所以－f(2)－f(1)－3＝f(1)＋f(2)＋3.即2(f(1)＋f(2))＝－6，f(1)＋f(2)＝－3.(3)因为f(x)＝(m－2)x2－3mx＋1为偶函数，所以－3m＝0，解得m＝0，所以f(x)＝－2x2＋1，它的单调递增区间是(－∞，0].
[错因分析]　要判断函数的奇偶性，必须先求函数定义域(看定义域是否关于原点对称)．有时还需要在定义域制约条件下将f(x)进行变形，以利于判定其奇偶性．
[错因分析]　错解忽略了函数的定义域关于原点对称这一条件，即－2b＋3b－1＝0.[正解]　∵f(x)是偶函数，∴f(－x)＝f(x)，即a＝0.又定义域为[－2b,3b－1]，∴－2b＋3b－1＝0，∴b＝1，∴f(x)＝x2＋1，x∈[－2,2]，∴函数f(x)的值域为[1,5]．
[答案]　B[解析]　①④为奇函数，②的定义域关于原点不对称，③不满足奇函数定义．
[答案]　B[解析]　奇函数的图象关于原点对称，偶函数的图象关于y轴对称，由图可知只有选项B符合．
[答案]　D[解析]　∵－f(a)＝f(－a)，∴点(－a，－f(a))在y＝f(x)的图象上，故选D.
[答案]　x|x＋2|[解析]　∵x<0，∴－x>0.∴f(x)＝－f(－x)＝－(－x)|－x－2|＝x|x＋2|，∴f(x)＝x|x＋2|.