- 专题12 幂函数(讲) 教案 15 次下载
- 专题11 函数的基本性质(奇偶性)(练) 教案 13 次下载
- 专题10 函数的基本性质(单调性)(练) 教案 17 次下载
- 专题10 函数的基本性质(单调性)(讲) 教案 18 次下载
- 专题09 函数的概念及其表示(练) 教案 16 次下载
高中数学人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质教学设计及反思
展开《2020-2021学年高一数学同步讲练测(新教材人教A版必修第一册)》
专题11函数的基本性质(奇偶性)(讲)
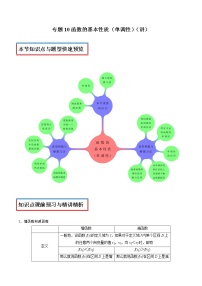
本节知识点与题型快速预览 |
知识点课前预习与精讲精析 |
函数的奇偶性
奇偶性 | 偶函数 | 奇函数 |
条件 | 对于f(x)定义域内的任意一个x | |
结论 | f(-x)=f(x) | f(-x)=-f(x) |
图象特点 | 关于y轴对称 | 关于原点对称 |
[知识点拨] (1)奇、偶函数定义域的特点.
由于f(x)和f(-x)须同时有意义,所以奇、偶函数的定义域关于原点对称.
(2)奇、偶函数的对应关系的特点.
①奇函数有f(-x)=-f(x)⇔f(-x)+f(x)=0⇔=-1(f(x)≠0);
②偶函数有f(-x)=f(x)⇔f(-x)-f(x)=0⇔=1(f(x)≠0).
(3)函数奇偶性的三个关注点.
①若奇函数在原点处有定义,则必有f(0)=0.有时可以用这个结论来否定一个函数为奇函数;
②既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空集合;
③函数根据奇偶性可分为奇函数、偶函数、既奇又偶函数、非奇非偶函数.
(4)奇、偶函数图象对称性的应用.
①若一个函数的图象关于原点对称,则这个函数是奇函数;
②若一个函数的图象关于y轴对称,则这个函数是偶函数.
1.已知,分别是定义在上的偶函数和奇函数,且,则( )
A.-3 B.-1 C.1 D.3
2.下列图像表示的函数中具有奇偶性的是( ).
A. B. C. D.
3.对于定义在上的任意奇函数,均有( )
A. B.
C. D.
4.已知函数为上的偶函数,当时,单调递减,若,则的取值范围是( )
A. B. C. D.
5.已知函数,若,则的值为( )
A. B. C. D.
典型题型与解题方法 |
重要考点一:函数奇偶性的判断
【典型例题】根据定义,判断下列函数的奇偶性:
(1);(2)g(x)=x4+2;
(3);(4).
【题型强化】判断下列函数的奇偶性.
(1)f(x)=2x+;
(2)f(x)=2-|x|;
(3)f(x)=+;
(4)f(x)=.
【收官验收】判断函数f(x)=x+ (a为常数)的奇偶性,并证明你的结论.
【名师点睛】
判断函数奇偶性的方法
(1)定义法:
(2)图象法:即若函数的图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.此法多用在解选择题、填空题中.
重要考点二:奇、偶函数图象的应用
【典型例题】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,
(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
【题型强化】已知奇函数f(x)定义域为[-5,5]且在[0,5]上的图象如图所示,求使f(x)<0的x的取值范围.
【收官验收】已知函数是定义在上的奇函数,当时,.
(1)求的解析式;
(2)作出函数的图象并求出单调增区间.
【名师点睛】
1.研究函数图象时,要注意对函数性质的研究,这样可避免作图的盲目性和复杂性.
2.利用函数的奇偶性作图,其依据是奇函数图象关于原点对称,偶函数图象关于y轴对称.
重要考点三:利用函数的奇偶性求解析式
【典型例题】若函数在上是奇函数,则的解析式为______.
【题型强化】已知函数是定义在上的奇函数,且时,,则时,________
【收官验收】已知函数是奇函数,且,则函数的解析式________.
【名师点睛】
利用函数奇偶性求函数解析式
利用函数奇偶性求函数解析式的关键是利用奇偶函数的关系式f(-x)=-f(x)或f(-x)=f(x)成立,但要注意求给定哪个区间的解析式就设这个区间上的变量为x,然后把x转化为-x(另一个已知区间上的解析式中的变量),通过适当推导,求得所求区间上的解析式.
重要考点四:忽略函数奇偶性对定义域的限制条件导致判断错误
【典型例题】已知定义在上的函数是增函数.
(1)若,求的取值范围;
(2)若函数是奇函数,且,解不等式.
【题型强化】已知函数是定义在上的奇函数,且.
(1)求函数的解析式;
(2)用定义法证明函数的单调性;
(3)若,求实数的取值范围.
【收官验收】定义在上的偶函数,当时单调递增,设,求m的取值范围.
【名师点睛】
1.函数y=f(x)是奇函数或偶函数的一个必不可少的条件是定义域关于原点对称.
2.确定函数的定义域时,要针对函数的原解析式.
重要考点五:逻辑推理与转化思想的应用——再谈恒成立问题
【典型例题】已知函数.
(1)写出一个奇函数和一个偶函数,使=+;
(2) 若对于任意的 恒成立,求实数的取值范围.
【题型强化】已知是定义在上的奇函数,且,若,时,都有.
(1)解关于的不等式;
(2)若对任意,,不等式恒成立,求实数的取值范围.
【收官验收】已知是定义在上的奇函数且单调递增,.
(1)解不等式:;
(2)若对所有,恒成立,求实数t的取值范围.
【名师点睛】
1.在我们数学研究中,存在大量的恒成立问题,如:
(1)f(x)在区间D上单调递增,则对任意x1,x2∈D,当x1<x2时,f(x1)<f(x2)恒成立;
(2)若f(x)是奇函数,定义域为M,则f(-x)=-f(x)对任意x∈M恒成立;若f(x)是偶函数,定义域为M,则对任意x∈M,f(-x)=f(x)恒成立;
(3)若f(x)的最大值为M,最小值为m,定义域为A,则对任意x∈A,有m≤f(x)≤M.
解答这类问题时,应充分利用其恒成立的特点选取解答方法.
2.遇到f(-x)与f(x)的关系问题时,应首先从函数f(x)的奇偶性入手考虑,如果f(x)不具有奇偶性,看是否存在奇(偶)函数g(x),使f(x)用g(x)表示,再利用g(x)的奇偶性来解答.
新高考数学一轮复习精品教案第05讲 函数的基本性质:单调性,奇偶性,周期性(含解析): 这是一份新高考数学一轮复习精品教案第05讲 函数的基本性质:单调性,奇偶性,周期性(含解析),共48页。教案主要包含了知识点总结,典型例题,技能提升训练等内容,欢迎下载使用。
专题11 圆锥曲线(亮点讲): 这是一份专题11 圆锥曲线(亮点讲),文件包含专题11圆锥曲线亮点讲解析版docx、专题11圆锥曲线亮点讲原卷版docx等2份教案配套教学资源,其中教案共102页, 欢迎下载使用。
数学必修11.3.2奇偶性教学设计: 这是一份数学必修11.3.2奇偶性教学设计,共4页。教案主要包含了学习导航,精典范例等内容,欢迎下载使用。