2020-2021学年18.1.2 平行四边形的判定教学课件ppt

这是一份2020-2021学年18.1.2 平行四边形的判定教学课件ppt，共26页。PPT课件主要包含了对边相等，对角线互相平分，对角相等，学习目标，还有什么判定方法呢，∴ADBC，AFD，平行四边形的判定，判定1，判定2等内容，欢迎下载使用。

两组对边分别平行的四边形叫做平
平行四边形的定义 行四边形.
如图：∵AB//CD，AD//BC，∴四边形ABCD是平行四边形.
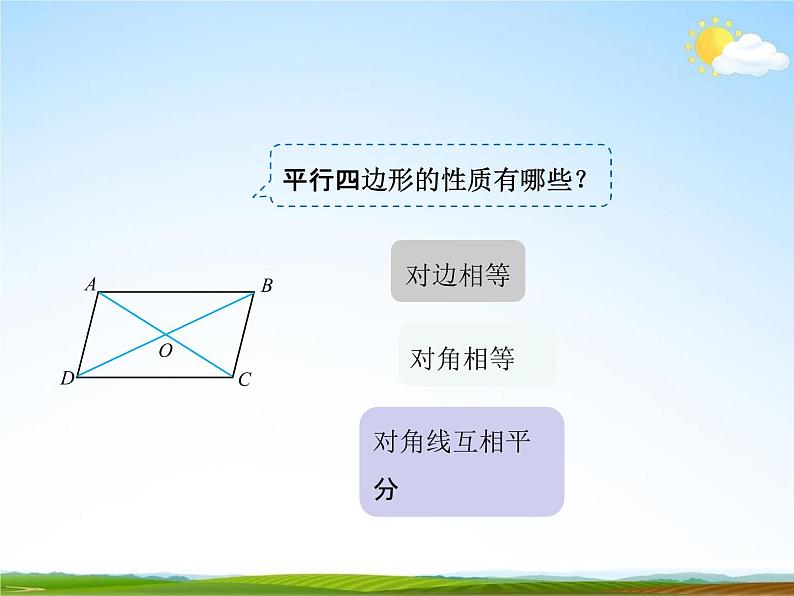
平行四边形的性质有哪些？
探索并证明平行四边形的判定定理.能熟练运用平行四边形的判定定理去计算 和证明.
思考 请写出平行四边形对边相等的逆命题.
如果一个四边形是平行四边形，那么它的两组对边相等.如果一个四边形的两组对边分别相等，那么这个四边 形是平行四边形.这个逆命题是真命题吗？
知识点：平行四边形的判定
平行四边形的判定1（定义法）： 两组对边分别平行的四边
形是平行四边形.数学语言：
∵ AB//CD、AD//BC∴四边形ABCD是平行四边形
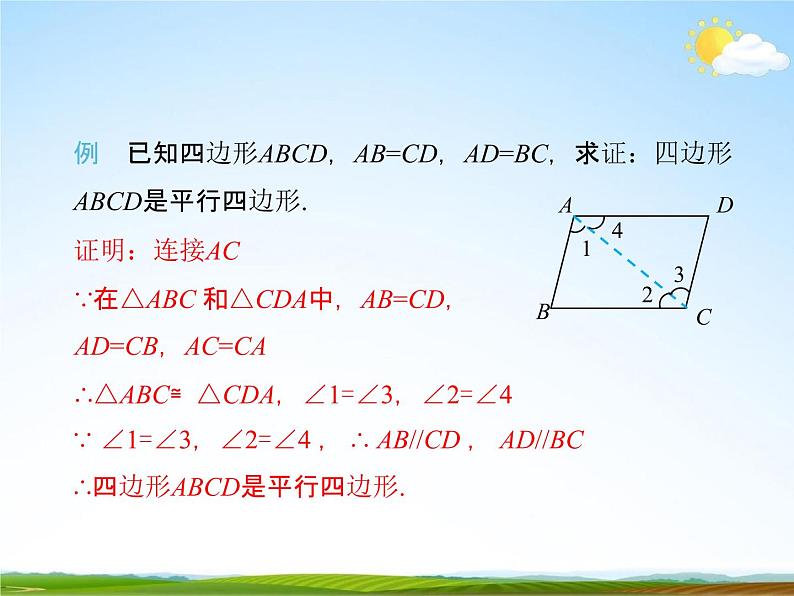
例已知四边形ABCD，AB=CD，AD=BC，求证：四边形
ABCD是平行四边形.证明：连接AC
∵在△ABC 和△CDA中，AB=CD，AD=CB，AC=CA∴△ABC≌△CDA，∠1=∠3，∠2=∠4∵ ∠1=∠3，∠2=∠4 ， ∴ AB//CD ， AD//BC∴四边形ABCD是平行四边形.
平行四边形的判定2：两组对边分别相等的四边形是平行四边形.
数学语言：∵ AB=CD、AD=BC∴四边形ABCD是平行四边形
通过以上例题，你能总结出什么 判定方法呢？
1.正确填写下列空格.
若AB//CD，补充 形ABCD是平行四边形.若AB=CD，补充 形ABCD是平行四边形.
AD//BC ，使得四边A
AD=BC ，使得四边 B
2. 将两个含有30°角的直角三角板按如图所示摆放，则 四边形ABCD是平行四边形，请说明理由.
解：∵ ∠ADB=∠CBD=30〫∴ AD//BC∵ ∠ABD=∠CDB=90〫∴ AB//CD∴四边形ABCD是平行四边形
1.如图，在四边形ABCD中， ∠1=∠2， ∠3=∠4，求证：
四边形ABCD是平行四边形.
证明： ∵∠1=∠2，∠3=∠4
∴ AB//CD ， AD//BC
∴四边形ABCD是平行四边形
2.如图，已知在四边形ABCD中，AE⊥BD于点E，CF⊥BD于 点F，AE=CF，BF=DE，求证：四边形ABCD是平行四边形.
证明：∵AE⊥BD于点E，CF⊥BD于点F，∴∠AED=∠CFB=90°，∵BF=DE，
∴BD-BF=BD-DE，即DF=BE，
∴△ADE≌△CBF（SAS），
3.如图，在三角形ABC中， AB=AC，点D是BC上任意一 点，DE平行AC交AB于点E， DF平行AB交AC于点F. 求证：
DE+DF=AC.证明：∵DE//AC ， DF//AB∴四边形AEDF是平行四边形，DE=AF
∵AB=AC∵DF//AB
∴∠B=∠C∴∠B=∠FDC∵∠C=∠FDC∴DF=CF
∵DE=AF，DF=CF∴ DE+DF=AF+CF=AC
4.如图，在平行四边形ABCD中， BE=DF. 求证：四边形
AECF是平行四边形.
证明：∵四边形ABCD是平行四边形∴AB=CD， ∠B=∠D
∵在△ABE 和△CDF中AB=CD， ∠B=∠D， BE=DF
∴△ABE≌△CDF(SAS)， ∠AEB=∠CFD
∵四边形ABCD是平行四边形
∴AD//BC， ∠CFD=∠FCB∴∠AEB=∠FCB
∴AE//CF∵ AE//CFAF//CE∴四边形AECF是平行四边形
两组对边分别平行的四边 形是平行四边形.
两组对边分别相等的四 边形是平行四边形.
1.如图，AD⊥AC，BC⊥AC，且AD=BC. 求证：四边形ABCD 是平行四边形.
解析：根据已知条件可得两个直角三角形 全等，进而得到结论AB=CD，通过“两组 对边相等” 判定该四边形是平行四边形.
证明：在 Rt△ABC 和 Rt△CDA 中
∴ Rt△ABC≌Rt△CDA
2.如图，在Rt△MON中，∠MNO=90〫，PN=5，MN=4，
MO-ON=2，PM+MO=8. 求证：四边形PMON是平行四边形.
解析：根据题目中的已知条件和 勾股定理可以求出四边形四边的 长度，由“两组对边分别相等” 判断该四边形是平行四边形.
证明： ∵在Rt△MON中，∠MNO=90〫，
∴四边形PMON是平行四边形
3. 如图，在△ABC中，分别以AB，AC，BC为边在BC的同侧 作等边△ACD，等边△ABE，等边△BCF. 试说明四边形 ADFE是平行四边形.解析：根据等边三角形的性质和三角 形的全等得出四边形ADFE的两组对 边相等，进而判定是平行四边形.
解： ∵ △BCF，△ABE都是等边三角形∴∠EBF+∠FBA=∠FBA+∠ABC=60 〫，∴∠EBF=∠ABC∵ EB=AB，∠EBF=∠ABC，BF=BC∴△ABC≌△EBF，EF=AC∵ △ACD是等边三角形∴ AC=AD，EF=AD
同理可得：△ABC≌△DFC，AB=DF∵△ABE是等边三角形∴ AB=AE，DF=AE∵ EF=AD，DF=AE∴四边形ADFE为平行四边形
请完成课本后练习第1题。