八年级下册18.1.2 平行四边形的判定教学课件ppt

这是一份八年级下册18.1.2 平行四边形的判定教学课件ppt，共25页。PPT课件主要包含了∴OBOD，学习目标，证明连接AC，∴EBFD，一组对边平行且相等，两组对边分别平行，∠B+∠A180°，ADBC，平行四边形的判定，判定5等内容，欢迎下载使用。

对角线互相平分的四边形是平行四
平行四边形的判定4 边形.
数学语言∵ OA=OC、OB=OD∴四边形ABCD是平行四边形
如图，在平行四边形ABCD中，点E、F分别在边AB、CD上， EF与BD相交于点O， OE=OF. 求证：四边形BFDE是平行四 边形.证明： ∵四边形ABCD是平行四边形
∵ OE=OF∴四边形BFDE是平行四边形
探索并证明平行四边形的判定定理.能熟练运用平行四边形的判定定理去计算 和证明.
思考 取两根长度相等的木棍，将它们平行放置，再用两 根木棍将其固定，得到的四边形是平行四边形吗？
猜想:一组对边平行且相等的 四边形是平行四边形.你能证明这个猜想吗？
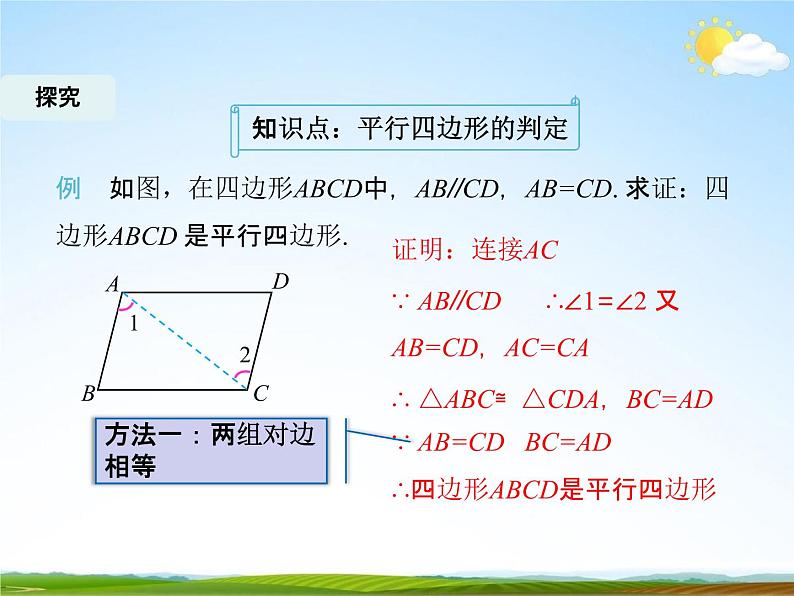
例如图，在四边形ABCD中，AB//CD，AB=CD. 求证：四
边形ABCD 是平行四边形.
∵ AB//CD∴∠1=∠2 又 AB=CD，AC=CA∴ △ABC≌△CDA，BC=AD∵ AB=CDBC=AD∴四边形ABCD是平行四边形
C方法一：两组对边 相等
知识点：平行四边形的判定
∵ AB//CD∴∠1=∠2∵ AB=CD，∠1=∠2，AC=CA∴ △ABC≌△CDA， ∠ACB=∠CAD∴ AD//BC又∵ AB//CD∴四边形ABCD是平行四边形
例如图，在四边形ABCD中，AB//CD，AB=CD.求证：四 边形ABCD是平行四边形.证明：连接AC
方法二：两组对边 平行
一组对边平行且相等的四边形是平行四边形.
数学语言：∵ AB//CD，AB=CD,∴四边形ABCD是平行四边形
例4如图，在平行四边形ABCD中，E、F分别是AB、CD的
中点. 求证：四边形EBFD是平行四边形.证明： ∵四边形ABCD是平行四边形∴ AB=CD， EB//FD∵ E、F分别是AB、CD的中点
∴四边形EBFD是平行四边形
不一定，如等腰梯形，其中AD//BC，AB=CD.
思考 一组对边平行，另外一组对边相等的四边形一定是 平行四边形吗？如果不是，请举例说明.
训练1.下列条件中，能判定四边形是平行四边形的是（ C ）. A.一组对边相等.一组对边平行.一组对边平行且相等.一组对边平行，另外一组对边相等.
2. 如图，已知平行四边形ABCD中，E、F分别是AB、CD上的 点，AF=CE. 求证：四边形DEBF是平行四边形.
证明： ∵ 四边形ABCD是平行四边形∴ AD=BC， AD//BD∵ AF=CE∴ DF=AD-AF，BE=BC-CE
∴ DF=BE， DF//BE∴四边形DEBF是平行四边形
1.如图，在四边形ABCD中，AB∥CD，要使四边形ABCD
A．AB＝CD B．BC＝ADC．∠A＝∠C D．BC∥AD
是平行四边形，可添加的条件不正确的是(B) A
2.如图，在四边形ABCD中，对角线 AC、BD 相交于点 O， OA=OC. BA⊥AC，DC⊥AC. 求证：四边形 ABCD 是平行四 边形.
解析：通过两个垂直可以得到 AB//CD，通过三角形的全等能 得到 AB=CD .
证明：∵ BA⊥AC，DC⊥AC
∴∠BAC=∠DCA=90〫
∵在△AOB和△COD中，∠BAC=∠DCA，OA=OC，∠AOB=∠COD
∴ △AOB≌△COD，AB=CD∵∠BAC=∠DCA=90〫∴ AB//CD∴四边形ABCD是平行四边形
3.如图，在平行四边形ABCD中，E、F 分别是AB、CD的 中点.求证：EF//AD//BC.
证明： ∵四边形ABCD是平行四边形∴AB=CD，AB//CD∵ E、F分别是AB、CD的中点∴AE=DF，AE//DF∴四边形AEFD是平行四边形
∴ AD//EF∵ AD//BC
∴ EF//AD//BC
4.如图，四边形ABCD和四边形AEFD都是平行四边形，求 证：四边形BCFE是平行四边形.
证明： ∵四边形ABCD是平行四边形∴AD=BC，AD//BC
∵四边形AEFD是平行四边形∴AD=EF，AD//EF∴BC=EF，BC//EF∴四边形BCFE是平行四边形
一组对边平行且相等的四 边形是平行四边形.
∵ AB//CD，AB=CD，∴四边形ABCD是平行四边形
1.如图，在四边形 BFDE 中，四边形 ABCD 是平行四边形，
AE=CF. 求证：四边形 BFDE 是平行四边形.证明：∵四边形ABCD是平行四边形
∴AB=CD，AB//CD
∵AE=CF，BE=AE+AB， DF=CF+CD∴ BE=DF∵ AB//CD∴ BE//DF∴ 四边形BFDE是平行四边形
2.如图，已知BE//DF，∠ADF=∠CBE，AF=CE. 求证：四边
形DEBF 是平行四边形.证明： ∵ BE//DF∴ ∠AFD=∠CEB又 ∠ADF=∠CBE， AF=CE∴△ADF≌△CBE，DF=BE 又 BE//DF∴ 四边形DEBF 是平行四边形
因混淆平行四边形的判定条件而出错
本题利用已知条件证明△ADE≌△CBF，得到DE=BF，然 后直接由已知条件“BE//DF”得四边形DEBF是平行四边 形.这里混淆了平行四边形的判定条件，误以为只要四边 形有一组对边平行，一组对边相等便是平行四边形.
3.如图，在平行四边形ABCD中，E、F分别为边AD、BC的中 点，对角线AC分别交BE、DF于点G、H. 求证：AG=CH.
证明： ∵四边形ABCD是平行四边形∴AD//BC
∴∠ADF=∠CFH， ∠EAG=∠FCH∵E、F分别为边AD、BC的中点
∴DE//BF， DE=BF
∵在△AEG和△CFH中， ∠AEG=∠CFH，AE=CF， ∠EAG=∠FCH∴ △AEG≌△CFH∴ AG=CH
∴四边形BFDE是平行四边形∴∠AEG=∠ADF∵∠ADF=∠CFH∴∠AEG=∠CFH
请完成课本后习题第4题。