鲁教版 (五四制)七年级下册1 二元一次方程组课文ppt课件

这是一份鲁教版 (五四制)七年级下册1 二元一次方程组课文ppt课件，共60页。PPT课件主要包含了二元一次方程组，题目大意，想一想，考考你，第一关，第三关，学习目标，新知探究，随堂练习，课堂小结等内容，欢迎下载使用。

列一元一次方程解应用题的步骤是什么？
2.设未知数，找等量关系；
1.能根据具体问题中的数量关系，列出二元一次方程组解决简单的实际问题；2.在解决实际问题过程中，进一步体会方程（组）是刻画现实世界的有效的数学模型，培养数学应用能力。
《孙子算经》是我国古代一部较为普及的算书，许多问题浅显有趣，其中下卷第31题“雉兔同笼”流传尤为广泛，飘洋过海流传到了日本等国。
“鸡兔同笼”题为: 今有鸡兔同笼， 上有三十五头， 下有九十四足， 问鸡兔各几何？
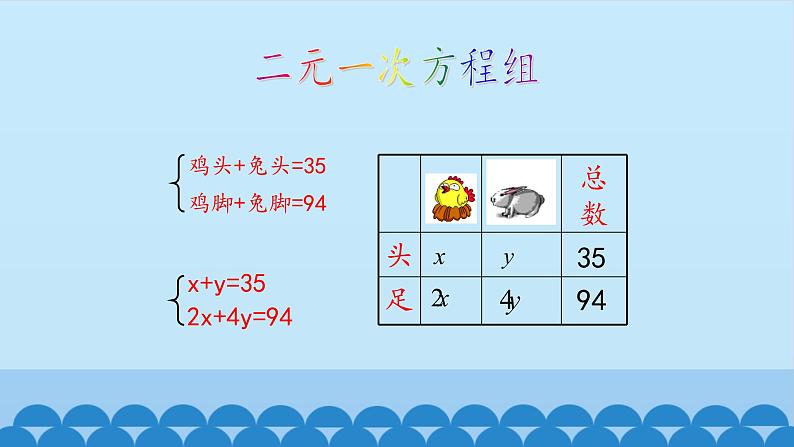
解：设鸡为x只，兔为y只，则
①×2得：2x+2y=70 ③
把y=12代入①，得：x=23
答：有鸡23只，兔12只。
今有牛五、羊二，直金十两。牛二、羊五，直金八两。牛、羊各直金几何？
5头牛、2只羊共价值10两“金”；2头牛、5只羊共价值8两“金”。问每头牛、每只羊各价值多少“金”？
设每头牛价值为x两，每只羊价值y两。
解：设每头牛值“金”x两，每头羊值“金”y两，由题意，得
以绳测井若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺。绳长、井深各几何？
用绳子测量水井的深度。如果将绳子折成三等份，一份绳长比井深多5尺；如果将绳子折成四等份，一份绳长比井深多1尺。绳长、井深各是多少尺？
解：设绳长x尺，井深y尺，由题意，得
答：绳长48尺，井深11尺。
答：绳长48尺，井深11尺。
古有一捕快，一天晚上他在野外的一个茅屋里，听到外边来了一群人在吵闹，他隐隐约约地听到几个声音，下面有这一古诗为证：
隔壁听到人分银，不知人数不知银。只知每人五两多六两，每人六两少五两，问你多少人数多少银？
1.设甲数为x，乙数为y，则“甲数的二倍与乙数的一半的和是15”，列出方程为____________。2.小刚有5角硬币和1元硬币各若干枚，币值共有六元五角，设5角有x枚，1元有y枚，列出方程为_____________。
1.某车间有工人54人，每人平均每天加工轴杆15个或轴承24个，一个轴杆与两个轴承配成一套。若分配x个工人加工轴杆，y个工人加工轴承，正好使每天加工的产品成套，则可列方程组为（　）。
有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食。树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子是整个鸽群的三分之一；若从树上飞下去一只，则树上、树下鸽子就一样多了。”你知道树上、树下各有多少只鸽子吗？
甲、乙两人赛跑，若乙先跑10米，甲跑5秒即可追上乙；若乙先跑2秒，则甲跑4秒就可追上乙。设甲速为x米/秒，乙速为y米/秒，则可列方程组为（　 ）。
（1）审题；（2）设两个未知数，找两个等量关系；（3）根据等量关系列方程，联立方程组；（4）解方程组；（5）检验并作答。
列二元一次方程组解应用题的步骤是什么？
1.会用列表的方式分析题中已知量与未知量的关系，列出相应的二元一次方程组；2.加强列方程组的技能训练，形成解决实际问题的一般性策略。
同学们，你知道你的生活有哪些必要的开支吗？
经济生活在我们生活中多么重要！你想运用数学知识使你的生活更加合理优化，更加幸福惬意吗？
新年来临爸爸想送小明一个书包和随身听作为新年礼物。爸爸对小明说：“我在家乐福、人民商场都发现同款的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元，你能说出随身听和书包单价各是多少元，那么我就买给你做新年礼物”。 你能帮助他吗？
设书包单价为x元，则随身听单价为y元，根据题意可列出方程：
答：书包单价92元，随身听单价360元。
例1.某公司去年的利润（总产值-总支出）为200万元。今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元。去年的总产值、总支出各是多少万元？
去年的总产值-去年的总支出=200万元，
今年的总产值-今年的总支出=780万元。
今年的总产值=去年总产值×（1+20%）
今年的总支出=去年的总支出×（1-10%）
分析：设去年的总产值为x万元，总支出为y元。
某公司去年的利润（总产值-总支出）为200万元。今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元。去年的总产值、总支出各是多少万元？
解：设去年的总产值为x万元，总支出为y万元，则今年的总产值=（1+20%）x万元，　今年的总支出=（1-10%）y万元。由题意得:
答：去年的总收入为2000万元，总支出为1800万元。
例2.医院用甲、乙两种原料为手术后的病人配制营养品。每克甲原料含0.5单位蛋白质和1单位铁质，每克乙原料含0.7单位蛋白质和0.4单位铁质。若病人每餐需要35单位蛋白质和40单位铁质，那么每餐甲、乙两种原料各多少克恰好满足病人的需要？
每餐甲原料中含蛋白质量=0.5×每餐甲原料的质量
每餐乙原料中含蛋白质量=0.7×每餐乙原料的质量
每餐甲原料中含蛋白质量+每餐乙原料中含蛋白质量=35
每餐甲原料中含铁质量=1×每餐甲原料的质量
每餐乙原料中含铁质量=0.4×每餐乙原料的质量
每餐甲原料中含铁质量+每餐乙原料中含铁质量=40
设每餐需要甲、乙两种原料各x，y克，则有下表:
由上表可以得到的等式：
答：每餐需甲原料28克，乙原料30克。
1.图表分析有利于理清题中的未知量，已知量以及等量关系；2.借助方程组解决实际问题。
1.一、二两班共有100名学生，他们的体育达标率（达到标准的百分率）为81%。如果一班学生的体育达标率为87.5%，二班的达标率为75%，那么一、二两班的学生数各是多少？
设一、二两班学生数分别为x名，y名，填写下表并求出x、y值。
答：一班有学生48名，二班有学生52名。
2.甲、乙两人从相距36千米的两地相向而行。如果甲比乙先走2时，那么他们在乙出发2.5时后相遇；如果乙比甲先走2时，那么他们在甲出发3时后相遇。甲、乙两人每时各走多少千米？
设甲、乙两人每时分别行走x千米、y千米，填写下表并求出x，y的值。
答：甲每时行走6千米，乙每时行走3.6千米。
活动规则： 四个同学一组编题，互评；然后推选出有创意，符合实际生活的例子进行全班交流。
1.在很多实际问题中，都存在着一些等量关系，因此，我们往往可以借助列方程或方程组的方法来处理这些问题。2.这种处理问题的过程可以进一步概括为：　　　　 分析　　　　　　 求解　　问题　　　　方程（组）　　　解答　　　　 抽象　　　　　　 检验3.要注意的是，处理实际问题的方法是多种多样的，图表分析是一种直观简洁的方法，应根据具体问题灵活选用。
（1）一个两位数，个位数字是a，十位数字是b，则这个两位数用代数式表示为 ，若交换个位和十位上的数字，得到一个新的两位数用代数式表示为 。 （2）一个两位数，个位上的数为x，十位上的数为y，如果在它们之间添上一个0，就得到一个三位数，这个三位数用代数式可以表示为 。 （3）有两个两位数a和b，如果将a放在b的左边，就得到一个四位数，那么这个四位数用代数式表示为 ；如果将a放在b的右边，将得到一个新的四位数，那么这个四位数用代数式可表示为 。
1.用二元一次方程组解决“里程碑上的数”这一有趣场景中的数字问题和行程问题；2.归纳出列二元一次方程组解决实际问题的一般步骤；3.初步体会列方程组解决实际问题的步骤，将实际问题转化成二元一次方程组的数学模型。
小明爸爸骑着摩托车带着小明在公路上匀速行驶，下图是小明每隔1小时看到的里程情况。你能说出小明在12:00时看到的里程碑上的数吗？
是一个两位数字，它的两个数字之和为7。
十位与个位数字与12:00时所看到的正好互换了。
比12:00时看到的两位数中间多了个0。
如果设小明在12:00时看到的数的十位数字是x，个位数字是y，那么
（1）12:00时小明看到的数可表示为 ，
根据两个数字和是7，可列出方程 。
（10y+x）-（10x+y）
（2）13:00时小明看到的数可表示为 ，
12:00～13:00间摩托车行驶的路程是 。
（100x+y）-（10y+x）
（3）14:00时小明看到的数可表示为 ，
13:00～14:00间摩托车行驶的路程是 。
12：00时是一个两位数，它的两个数字之和为7；13：00时十位与个位数字与12：00所看到的正好互换了；14：00比12：00时看到的两位数中间多了个0。
（4）12:00～13:00与13:00～14:00两段时间内摩托车的行驶路程有什么关系？你能列出相应的方程吗？
解：如果设小明在12:00时看到的数的十位数字是x，个位数字是y，那么根据以上分析，得方程组：
答：小明在12:00时看到的里程碑上的数是16。
列二元一次方程解决实际问题的一般步骤： 审： 设： 列： 解： 验： 答：
审清题意，找出等量关系。
设未知数（直接、间接）。
根据等量关系，列出方程组。
解方程组，求出未知数。
检验所求出未知数是否符合题意。
例：两个两位数的和是68，在较大的两位数的右边接着写较小的两位数，得到一个四位数；在较大的两位数的左边写上较小的两位数，也得到一个四位数。已知前一个四位数比后一个四位数大2178，求这两个两位数。
分析：设较大的两位数为x，较小的两位数为y，在较大数的右边接着写较小的数，所写的数可表示为 ；在较大数的左边接着写上较小的数，所写的数可表示为 。
解：设较大的两位数为x，较小的两位数为y，则有：
答：这两个两位数分别是45和23。
1．一个两位数，减去它的个位数字之和的3倍，结果是23；这个两位数除以它的个位数字之和，商是5，余数是1。这个两位数是多少？
解：设这个两位数的十位数为x，个位数为y，则有：
答：这个两位数是56。
56-3（5+6）=2356÷（5+6）=5.1
2．一个两位数是另一个两位数的3倍，如果把这个两位数放在另一个两位数的左边与放在右边所得的数之和为8484。求这个两位数。
通过这节课的学习，你有什么收获？
1.本节课主要研究有关数字问题和行程问题，解数字题的关键是设各位数字为未知数，用这些未知数表示相关数量，再列出方程。
2.用二元一次方程组解应用题一般步骤有六步： 审、设、列、解、验、答。