2021年中考数学三轮冲刺《函数压轴题》解答题冲刺练习(含答案)

这是一份2021年中考数学三轮冲刺《函数压轴题》解答题冲刺练习(含答案)，共18页。试卷主要包含了解得等内容，欢迎下载使用。

已知抛物线C1：y=a(x+1)2﹣2的顶点为A，且经过点B(﹣2，﹣1).
(1)求A点的坐标和抛物线C1的解析式；
(2)如图1，将抛物线C1向下平移2个单位后得到抛物线C2，且抛物线C2与直线AB相交于C，D两点，求S△OAC：S△OAD的值；
(3)如图2，若过P(﹣4，0)，Q(0，2)的直线为l，点E在(2)中抛物线C2对称轴右侧部分(含顶点)运动，直线m过点C和点E.问：是否存在直线m，使直线l，m与x轴围成的三角形和直线l，m与y轴围成的三角形相似？若存在，求出直线m的解析式；若不存在，说明理由.

若两条抛物线的顶点相同，则称它们为“友好抛物线”，抛物线C1：y1=－2x2＋4x＋2与C2：y2=－x2＋mx＋n为“友好抛物线”.
(1)求抛物线C2的解析式；
(2)点A是抛物线C2上在第一象限的动点，过A作AQ⊥x轴，Q为垂足，求AQ＋OQ的最大值.
(3)设抛物线C2的顶点为C，点B的坐标为(－1，4)，问在C2的对称轴上是否存在点M，使线段MB绕点M逆时针旋转90°得到线段MB′，且点B′恰好落在抛物线C2上？若存在求出点M的坐标，不存在说明理由.
如图，已知抛物线y=ax2+bx+c图象经过A（-2,0），B（6,0），C（0,4），D为顶点.
（1）求抛物线解析式；
（2）以顶点D为圆心，2为半径作⊙D，判断直线BC与⊙D的位置关系，并说明理由；
（3）在(2)的条件下，若P点为D上一动点，连PB，PC，设△PBC面积的最大值为S1，最小值为S2，
求的值.








如图，已知抛物线y=ax2+bx+5经过A(﹣5，0)，B(﹣4，﹣3)两点，与x轴的另一个交点为C，顶点为D，连结CD．
(1)求该抛物线的表达式；
(2)点P为该抛物线上一动点(与点B、C不重合)，设点P的横坐标为t．
①当点P在直线BC的下方运动时，求△PBC的面积的最大值；
②该抛物线上是否存在点P，使得∠PBC=∠BCD？若存在，求出所有点P的坐标；若不存在，请说明理由．
综合与探究
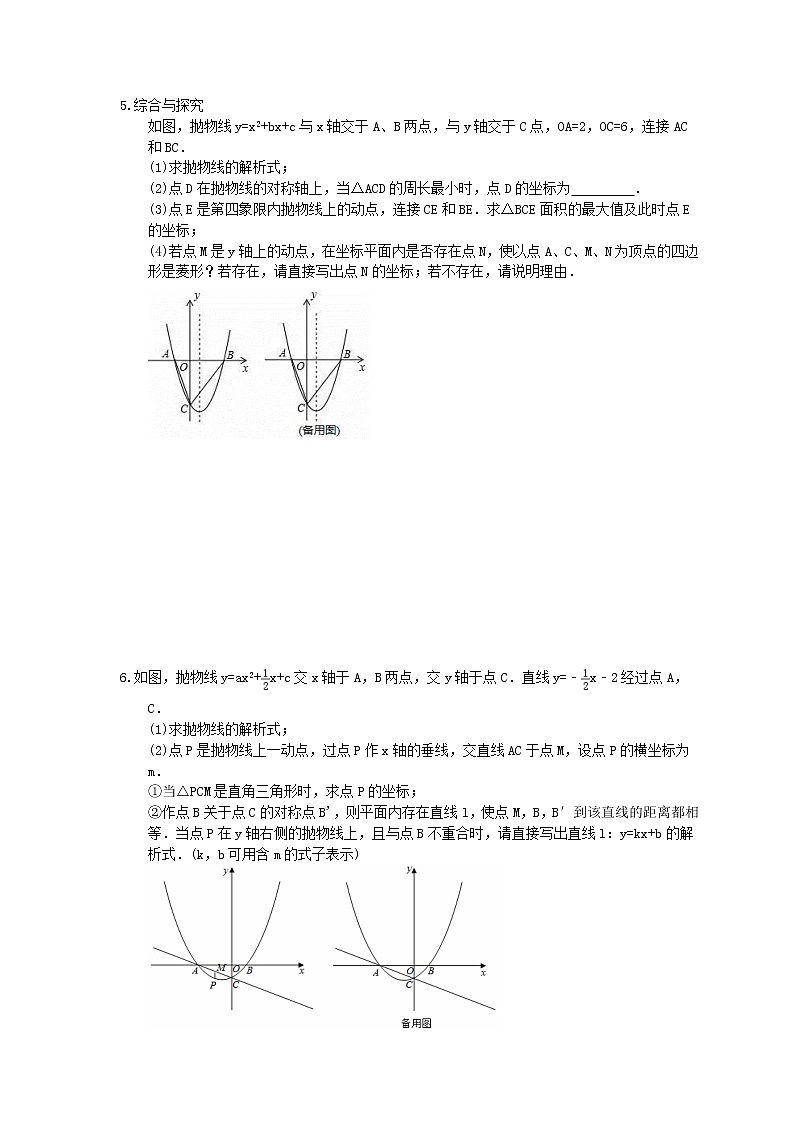
如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA=2，OC=6，连接AC和BC．
(1)求抛物线的解析式；
(2)点D在抛物线的对称轴上，当△ACD的周长最小时，点D的坐标为 ．
(3)点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；
(4)若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
如图，抛物线y=ax2+x+c交x轴于A，B两点，交y轴于点C．直线y=﹣x﹣2经过点A，C．
(1)求抛物线的解析式；
(2)点P是抛物线上一动点，过点P作x轴的垂线，交直线AC于点M，设点P的横坐标为m．
①当△PCM是直角三角形时，求点P的坐标；
②作点B关于点C的对称点B'，则平面内存在直线l，使点M，B，B′到该直线的距离都相等．当点P在y轴右侧的抛物线上，且与点B不重合时，请直接写出直线l：y=kx+b的解析式．(k，b可用含m的式子表示)
如图，在平面直角坐标系中，平行四边形OABC的顶点A，C的坐标分别为(6，0)，(4，3)，经过B，C两点的抛物线与x轴的一个交点D的坐标为(1，0)．
(1)求该抛物线的解析式；
(2)若∠AOC的平分线交BC于点E，交抛物线的对称轴于点F，点P是x轴上一动点，当PE+PF的值最小时，求点P的坐标；
(3)在(2)的条件下，过点A作OE的垂线交BC于点H，点M，N分别为抛物线及其对称轴上的动点，是否存在这样的点M，N，使得以点M，N，H，E为顶点的四边形为平行四边形？若存在，直接写出点M的坐标，若不存在，说明理由．
如图①，在平面直角坐标系xOy中，已知A(﹣2，2)，B(﹣2，0)，C(0，2)，D(2，0)四点，动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合)，设运动时间为t(秒)．
(1)求经过A、C、D三点的抛物线的解析式；
(2)点P在(1)中的抛物线上，当M为BC的中点时，若△PAM≌△PBM，求点P的坐标；
(3)当M在CD上运动时，如图②．过点M作MF⊥x轴，垂足为F，ME⊥AB，垂足为E．设矩形MEBF与△BCD重叠部分的面积为S，求S与t的函数关系式，并求出S的最大值；
(4)点Q为x轴上一点，直线AQ与直线BC交于点H，与y轴交于点K．是否存在点Q，使得△HOK为等腰三角形？若存在，直接写出符合条件的所有Q点的坐标；若不存在，请说明理由．
特例感知
(1)如图1，对于抛物线y1=﹣x2﹣x+1，y2=﹣x2﹣2x+1，y3=﹣x2﹣3x+1，下列结论正确的序号是 ；
①抛物线y1，y2，y3都经过点C(0，1)；
②抛物线y2，y3的对称轴由抛物线y1的对称轴依次向左平移个单位得到；
③抛物线y1，y2，y3与直线y=1的交点中，相邻两点之间的距离相等．
形成概念
(2)把满足yn=﹣x2﹣nx+1(n为正整数)的抛物线称为“系列平移抛物线”．
知识应用
在(2)中，如图2．
①“系列平移抛物线”的顶点依次为P1，P2，P3，…，Pn，用含n的代数式表示顶点Pn的坐标，并写出该顶点纵坐标y与横坐标x之间的关系式；
②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”：C1，C2，C3，…，∁n，其横坐标分别为﹣k﹣1，﹣k﹣2，﹣k﹣3，…，﹣k﹣n(k为正整数)，判断相邻两点之间的距离是否都相等，若相等，直接写出相邻两点之间的距离；若不相等，说明理由．
③在②中，直线y=1分别交“系列平移抛物线”于点A1，A2，A3，…，An，连接∁nAn，Cn﹣1An﹣1，判断∁nAn，Cn﹣1An﹣1是否平行？并说明理由．
如图，二次函数y=﹣x2+bx+c的图象过原点，与x轴的另一个交点为(8，0)
(1)求该二次函数的解析式；
(2)在x轴上方作x轴的平行线y1=m，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；
(3)在(2)的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒(t＞0)．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．
\s 0 参考答案
解：(1)∵抛物线C1：y=a(x+1)2﹣2的顶点为A，
∴点A的坐标为(﹣1，﹣2).
∵抛物线C1：y=a(x+1)2﹣2经过点B(﹣2，﹣1)，
∴a(﹣2+1)2﹣2=﹣1.解得：a=1.
∴抛物线C1的解析式为：y=(x+1)2﹣2.
(2)∵抛物线C2是由抛物线C1向下平移2个单位所得，
∴抛物线C2的解析式为：y=(x+1)2﹣2﹣2=(x+1)2﹣4.
设直线AB的解析式为y=kx+b.
∵A(﹣1，﹣2)，B(﹣2，﹣1)，
∴解得：
∴直线AB的解析式为y=﹣x﹣3.
联立解得：或.
∴C(﹣3，0)，D(0，﹣3).∴OC=3，OD=3.
过点A作AE⊥x轴，垂足为E，
过点A作AF⊥y轴，垂足为F，
∵A(﹣1，﹣2)，
∴AF=1，AE=2.
∴S△OAC：S△OAD=(OC•AE)：(OD•AF)=(×3×2)：(×3×1)=2.
∴S△OAC：S△OAD的值为2.
(3)设直线m与y轴交于点G，设点G的坐标为(0，t).
= 1 \* GB3 \* MERGEFORMAT ①当直线m与直线l平行时，则有CG∥PQ.
∴△OCG∽△OPQ.
∴=.
∵P(﹣4，0)，Q(0，2)，
∴OP=4，OQ=2，
∴=.∴OG=.
∵当t=时，直线m与直线l平行，
∴直线l，m与x轴不能构成三角形.
∴t≠.
= 2 \* GB3 \* MERGEFORMAT ②当直线m与直线l相交时，设交点为H，
①t＜0时，如图2①所示.
∵∠PHC＞∠PQG，∠PHC＞∠QGH，
∴∠PHC≠∠PQG，∠PHC≠∠QGH.
当∠PHC=∠GHQ时，
∵∠PHC+∠GHQ=180°，
∴∠PHC=∠GHQ=90°.
∵∠POQ=90°，
∴∠HPC=90°﹣∠PQO=∠HGQ.
∴△PHC∽△GHQ.
∵∠QPO=∠OGC，
∴tan∠QPO=tan∠OGC.
∴=.∴=.∴OG=6.
∴点G的坐标为(0，﹣6)
设直线m的解析式为y=mx+n，
∵点C(﹣3，0)，点G(0，﹣6)在直线m上，
∴.解得：.
∴直线m的解析式为y=﹣2x﹣6，
联立，解得：或∴E(﹣1，﹣4).
此时点E就是抛物线的顶点，符合条件.
∴直线m的解析式为y=﹣2x﹣6.
②当t=0时，此时直线m与x轴重合，
∴直线l，m与x轴不能构成三角形.
∴t≠0.
③O＜t＜1.5时，如图2②所示，
∵tan∠GCO==＜，tan∠PQO===2，
∴tan∠GCO≠tan∠PQO.∴∠GCO≠∠PQO.
∵∠GCO=∠PCH，
∴∠PCH≠∠PQO.
又∵∠HPC＞∠PQO，
∴△PHC与△GHQ不相似.
∴符合条件的直线m不存在.
④＜t≤2时，如图2③所示.
∵tan∠CGO==≥，tan∠QPO===.
∴tan∠CGO≠tan∠QPO.
∴∠CGO≠∠QPO.
∵∠CGO=∠QGH，
∴∠QGH≠∠QPO，
又∵∠HQG＞∠QPO，
∴△PHC与△GHQ不相似.
∴符合条件的直线m不存在.
⑤t＞2时，如图2④所示.
此时点E在对称轴的右侧.
∵∠PCH＞∠CGO，
∴∠PCH≠∠CGO.
当∠QPC=∠CGO时，
∵∠PHC=∠QHG，∠HPC=∠HGQ，
∴△PCH∽△GQH.
∴符合条件的直线m存在.
∵∠QPO=∠CGO，∠POQ=∠GOC=90°，
∴△POQ∽△GOC.
∴=.∴=.∴OG=6.
∴点G的坐标为(0，6).
设直线m的解析式为y=px+q
∵点C(﹣3，0)、点G(0，6)在直线m上，
∴.解得：.
∴直线m的解析式为y=2x+6.
综上所述：
存在直线m，使直线l，m与x轴围成的三角形和直线l，m与y轴围成的三角形相似，
此时直线m的解析式为y=﹣2x﹣6和y=2x+6.
解：(1)∵y1=－2x2＋4x＋2=－2(x－1)2＋4，
∴抛物线C1的顶点坐标为(1，4).
∵抛物线C1与C2顶点相同，
∴eq \f(－m,－1×2)=1，－1＋m＋n=4，解得m=2，n=3，
∴抛物线C2的解析式为y2=－x2＋2x＋3
(2)如图1，设点A的坐标为(a，－a2＋2a＋3).
∵AQ=－a2＋2a＋3，OQ=a，
∴AQ＋OQ=－a2＋2a＋3＋a=－a2＋3a＋3=－(a－eq \f(3,2))2＋eq \f(21,4).
∴当a=eq \f(3,2)时，AQ＋OQ有最大值，最大值为eq \f(21,4)
(3)如图2，连结BC，过点B′作B′D⊥CM，垂足为D.
∵B(－1，4)，C(1，4)，抛物线的对称轴为x=1，
∴BC⊥CM，BC=2.
∵∠BMB′=90°，
∴∠BMC＋∠B′MD=90°.
∵B′D⊥MC，
∴∠MB′D＋∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中，
eq \b\lc\{(\a\vs4\al\c1(∠MB′D＝∠BMC，,∠BCM＝∠MDB′，,BM＝MB′，))
∴△BCM≌△MDB′.
∴BC=MD，CM=B′D.
设点M的坐标为(1，a).则B′D=CM=4－a，MD=CB=2.
∴点B′的坐标为(a－3，a－2).
∴－(a－3)2＋2(a－3)＋3=a－2.
整理得a2－7a－10=0.解得a=2或a=5.
当a=2时，M的坐标为(1，2)，
当a=5时，M的坐标为(1，5).
综上所述，当点M的坐标为(1，2)或(1，5)时，B′恰好落在抛物线C2上.
解：（1）y=-1/3x2+4/3x+4；
（2）相离；
（3）比值为4.

解：
(1)将点A、B坐标代入二次函数表达式得：，解得：，
故抛物线的表达式为：y=x2+6x+5…①，
令y=0，则x=﹣1或﹣5，即点C(﹣1，0)；
(2)①如图1，过点P作y轴的平行线交BC于点G，
将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y=x+1…②，
设点G(t，t+1)，则点P(t，t2+6t+5)，
S△PBC=PG(xC﹣xB)=(t+1﹣t2﹣6t﹣5)=﹣t2﹣t﹣6，
∵＜0，∴S△PBC有最大值，当t=﹣时，其最大值为；
②设直线BP与CD交于点H，
当点P在直线BC下方时，
∵∠PBC=∠BCD，∴点H在BC的中垂线上，
线段BC的中点坐标为(﹣，﹣)，
过该点与BC垂直的直线的k值为﹣1，
设BC中垂线的表达式为：y=﹣x+m，将点(﹣，﹣)代入上式并解得：
直线BC中垂线的表达式为：y=﹣x﹣4…③，
同理直线CD的表达式为：y=2x+2…④，
联立③④并解得：x=﹣2，即点H(﹣2，﹣2)，
同理可得直线BH的表达式为：y=x﹣1…⑤，
联立①⑤并解得：x=﹣或﹣4(舍去﹣4)，
故点P(﹣，﹣)；
当点P(P′)在直线BC上方时，
∵∠PBC=∠BCD，∴BP′∥CD，
则直线BP′的表达式为：y=2x+s，将点B坐标代入上式并解得：s=5，
即直线BP′的表达式为：y=2x+5…⑥，
联立①⑥并解得：x=0或﹣4(舍去﹣4)，
故点P(0，5)；
故点P的坐标为P(﹣，﹣)或(0，5)．
解：
(1)∵OA=2，OC=6∴A(﹣2，0)，C(0，﹣6)
∵抛物线y=x2+bx+c过点A、C
∴ 解得：
∴抛物线解析式为y=x2﹣x﹣6
(2)∵当y=0时，x2﹣x﹣6=0，解得：x1=﹣2，x2=3
∴B(3，0)，抛物线对称轴为直线x=
∵点D在直线x=上，点A、B关于直线x=对称
∴xD=，AD=BD
∴当点B、D、C在同一直线上时，C△ACD=AC+AD+CD=AC+BD+CD=AC+BC最小
设直线BC解析式为y=kx﹣6∴3k﹣6=0，解得：k=2
∴直线BC：y=2x﹣6∴yD=2×﹣6=﹣5∴D(，﹣5)故答案为：(，﹣5)
(3)过点E作EG⊥x轴于点G，交直线BC与点F
设E(t，t2﹣t﹣6)(0＜t＜3)，则F(t，2t﹣6)
∴EF=2t﹣6﹣(t2﹣t﹣6)=﹣t2+3t
∴S△BCE=S△BEF+S△CEF=EF•BG+EF•OG=EF(BG+OG)=EF•OB
=×3(﹣t2+3t)=﹣(t﹣)2+
∴当t=时，△BCE面积最大 ∴yE=()2﹣﹣6=﹣
∴点E坐标为(，﹣)时，△BCE面积最大，最大值为．
(4)存在点N，使以点A、C、M、N为顶点的四边形是菱形．
∵A(﹣2，0)，C(0，﹣6)∴AC=
①若AC为菱形的边长，如图3，则MN∥AC且，MN=AC=2
∴N1(﹣2，2)，N2(﹣2，﹣2)，N3(2，0)
②若AC为菱形的对角线，如图4，则AN4∥CM4，AN4=CN4
设N4(﹣2，n)∴﹣n=解得：n=﹣∴N4(﹣2，﹣)
综上所述，点N坐标为(﹣2，2)，(﹣2，﹣2)，(2，0)，(﹣2，﹣)．
解：
(1)当x=0时，y=﹣x﹣2=﹣2，∴点C的坐标为(0，﹣2)；
当y=0时，﹣x﹣2=0，解得：x=﹣4，∴点A的坐标为(﹣4，0)．
将A(﹣4，0)，C(0，﹣2)代入y=ax2+x+c，得：，解得：，
∴抛物线的解析式为y=x2+x﹣2．
(2)①∵PM⊥x轴，∴∠PMC≠90°，∴分两种情况考虑，如图1所示．
(i)当∠MPC=90°时，PC∥x轴，∴点P的纵坐标为﹣2．
当y=﹣2时，x2+x﹣2=﹣2，解得：x1=﹣2，x2=0，
∴点P的坐标为(﹣2，﹣2)；
(ii)当∠PCM=90°时，设PC与x轴交于点D．
∵∠OAC+∠OCA=90°，∠OCA+∠OCD=90°，∴∠OAC=∠OCD．
又∵∠AOC=∠COD=90°，∴△AOC∽△COD，∴=，即=，
∴OD=1，∴点D的坐标为(1，0)．
设直线PC的解析式为y=kx+b(k≠0)，
将C(0，﹣2)，D(1，0)代入y=kx+b，得：
，解得：，∴直线PC的解析式为y=2x﹣2．
联立直线PC和抛物线的解析式成方程组，得：，
解得：，，点P的坐标为(6，10)．
综上所述：当△PCM是直角三角形时，点P的坐标为(﹣2，﹣2)或(6，10)．
②当y=0时，x2+x﹣2=0，解得：x1=﹣4，x2=2，∴点B的坐标为(2，0)．
∵点C的坐标为(0，﹣2)，点B，B′关于点C对称，
∴点B′的坐标为(﹣2，﹣4)．
∵点P的横坐标为m(m＞0且m≠0)，∴点M的坐标为(m，0)．
分三种情况考虑，如图2所示：
∴直线PB的解析式为y=(m+4)x﹣(m+4)(可利用待定系数求出)．
∵点B，B′关于点C对称，点B，B′，P到直线l的距离都相等，
∴直线l过点C，且直线l∥直线PB，
∴直线l的解析式为y=(m+4)x﹣2．
解：
(1)∵平行四边形OABC中，A(6，0)，C(4，3)
∴BC=OA=6，BC∥x轴
∴xB=xC+6=10，yB=yC=3，即B(10，3)
设抛物线y=ax2+bx+c经过点B、C、D(1，0)
∴ 解得：
∴抛物线解析式为y=﹣x2+x﹣
(2)如图1，作点E关于x轴的对称点E'，连接E'F交x轴于点P
∵C(4，3)∴OC=∵BC∥OA∴∠OEC=∠AOE
∵OE平分∠AOC∴∠AOE=∠COE∴∠OEC=∠COE∴CE=OC=5
∴xE=xC+5=9，即E(9，3)∴直线OE解析式为y=x
∵直线OE交抛物线对称轴于点F，对称轴为直线：x=﹣7∴F(7，)
∵点E与点E'关于x轴对称，点P在x轴上∴E'(9，﹣3)，PE=PE'
∴当点F、P、E'在同一直线上时，PE+PF=PE'+PF=FE'最小
设直线E'F解析式为y=kx+h
∴ 解得：∴直线E'F：y=﹣x+21
当﹣x+21=0时，解得：x=
∴当PE+PF的值最小时，点P坐标为(，0)．
(3)存在满足条件的点M，N，使得以点M，N，H，E为顶点的四边形为平行四边形．
设AH与OE相交于点G(t，t)，如图2
∵AH⊥OE于点G，A(6，0)∴∠AGO=90°∴AG2+OG2=OA2
∴(6﹣t)2+(t)2+t2+(t)2=62∴解得：t1=0(舍去)，t2=∴G(，)
设直线AG解析式为y=dx+e
∴ 解得：∴直线AG：y=﹣3x+18
当y=3时，﹣3x+18=3，解得：x=5∴H(5，3)
∴HE=9﹣5=4，点H、E关于直线x=7对称
①当HE为以点M，N，H，E为顶点的平行四边形的边时，如图2
则HE∥MN，MN=HE=4
∵点N在抛物线对称轴：直线x=7上∴xM=7+4或7﹣4，即xM=11或3
当x=3时，yM=﹣×9+×9﹣=∴M(3，)或(11，)
②当HE为以点M，N，H，E为顶点的平行四边形的对角线时，如图3
则HE、MN互相平分
∵直线x=7平分HE，点F在直线x=7上
∴点M在直线x=7上，即M为抛物线顶点
∴yM=﹣×49+×7﹣=4∴M(7，4)
综上所述，点M坐标为(3，)、(11，)或(7，4)．
解：
(1)设函数解析式为y=ax2+bx+c，
将点A(﹣2，2)，C(0，2)，D(2，0)代入解析式可得
，∴，∴y=﹣﹣x+2；
(2)∵△PAM≌△PBM，∴PA=PB，MA=MB，
∴点P为AB的垂直平分线与抛物线的交点，
∵AB=2，∴点P的纵坐标是1，
∴1=﹣﹣x+2，∴x=﹣1+或x=﹣1﹣，
∴P(﹣1﹣，1)或P(﹣1+，1)；
(3)CM=t﹣2，MG=CM=2t﹣4，
MD=4﹣(BC+CM)=4﹣(2+t﹣2)=4﹣t，
MF=MD=4﹣t，∴BF=4﹣4+t=t，
∴S= (GM+BF)×MF= (2t﹣4+t)×(4﹣t)=﹣+8t﹣8=﹣ (t﹣)2+；
当t=时，S最大值为；
(3)设点Q(m，0)，直线BC的解析式y=﹣x+2，
直线AQ的解析式y=﹣ (x+2)+2，
∴K(0，)，H(，)，
∴OK2=，OH2=+，HK2=+，
①当OK=OH时， =+，
∴m2﹣4m﹣8=0，∴m=2+2或m=2﹣2；
②当OH=HK时， +=+，
∴m2﹣8=0，∴m=2或m=﹣2；
③当OK=HK时， =+，不成立；
综上所述：Q(2+2，0)或Q(2﹣2，0)或Q(2，0)或Q(﹣2，0)；
解：
(1)①当x=0时，分别代入抛物线y1，y2，y3，即可得y1=y2=y3=1；①正确；
②y2=﹣x2﹣2x+1，y3=﹣x2﹣3x+1的对称轴分别为x=﹣1，x=﹣，
y1=﹣x2﹣x+1的对称轴x=﹣，
由x=﹣向左移动得到x=﹣1，再向左移动得到x=﹣，
②正确；
③当y=1时，则﹣x2﹣x+1=1，∴x=0或x=﹣1；﹣x2﹣2x+1=1，∴x=0或x=﹣2；
﹣x2﹣3x+1=1，∴x=0或x=﹣3；∴相邻两点之间的距离都是1，
③正确；故答案为①②③；
(2)①yn=﹣x2﹣nx+1的顶点为(﹣，)，令x=﹣，y=，∴y=x2+1；
②∵横坐标分别为﹣k﹣1，﹣k﹣2，﹣k﹣3，…，﹣k﹣n(k为正整数)，
当x=﹣k﹣n时，y=﹣k2﹣nk+1，
∴纵坐标分别为﹣k2﹣k+1，﹣k2﹣2k+1，﹣k2﹣3k+1，…，﹣k2﹣nk+1，
∴相邻两点间距离分别为；∴相邻两点之间的距离都相等；
③当y=1时，﹣x2﹣nx+1=1，∴x=0或x=﹣n，
∴A1(﹣1，1)，A2(﹣2，1)，A3(﹣3，1)，…，An(﹣n，1)，
C1(﹣k﹣1，﹣k2﹣k+1)，C2(﹣k﹣2，﹣k2﹣2k+1)，C3(﹣k﹣3，﹣k2﹣3k+1)，…，
∁n(﹣k﹣n，﹣k2﹣nk+1)，
∵=k+1， =k+1， =k+1，…，
=k+1，
∴∁nAn∥Cn﹣1An﹣1；
解：
(1)将(0，0)，(8，0)代入y=﹣x2+bx+c，得：
，解得：，
∴该二次函数的解析式为y=﹣x2+x．
(2)当y=m时，﹣x2+x=m，解得：x1=4﹣，x2=4+，
∴点A的坐标为(4﹣，m)，点B的坐标为(4+，m)，
∴点D的坐标为(4﹣，0)，点C的坐标为(4+，0)．
∵矩形ABCD为正方形，
∴4+﹣(4﹣)=m，解得：m1=﹣16(舍去)，m2=4．
∴当矩形ABCD为正方形时，m的值为4．
(3)以A、E、F、Q四点为顶点构成的四边形能为平行四边形．
由(2)可知：点A的坐标为(2，4)，点B的坐标为(6，4)，点C的坐标为(6，0)，
点D的坐标为(2，0)．
设直线AC的解析式为y=kx+a(k≠0)，
将A(2，4)，C(6，0)代入y=kx+a，得：
，解得：，∴直线AC的解析式为y=﹣x+6．
当x=2+t时，y=﹣x2+x=﹣t2+t+4，y=﹣x+6=﹣t+4，
∴点E的坐标为(2+t，﹣t2+t+4)，点F的坐标为(2+t，﹣t+4)．
∵以A、E、F、Q四点为顶点构成的四边形为平行四边形，且AQ∥EF，
∴AQ=EF，分三种情况考虑：
①当0＜t≤4时，如图1所示，AQ=t，EF=﹣t2+t+4﹣(﹣t+4)=﹣t2+t，
∴t=﹣t2+t，解得：t1=0(舍去)，t2=4；
②当4＜t≤7时，如图2所示，AQ=t﹣4，EF=﹣t2+t+4﹣(﹣t+4)=﹣t2+t，
∴t﹣4=﹣t2+t，解得：t3=﹣2(舍去)，t4=6；
③当7＜t≤8时，AQ=t﹣4，EF=﹣t+4﹣(﹣t2+t+4)=t2﹣t，
∴t﹣4=t2﹣t，解得：t5=5﹣(舍去)，t6=5+(舍去)．
综上所述：当以A、E、F、Q四点为顶点构成的四边形为平行四边形时，t的值为4或6．