2021学年2.4抛物线图文ppt课件

这是一份2021学年2.4抛物线图文ppt课件，共25页。PPT课件主要包含了对称性，离心率，y22px，AB2p，焦半径公式，焦半径，关于x轴对称，关于y轴对称，抛物线的几何性质，提升总结等内容，欢迎下载使用。

类比椭圆、双曲线的几何性质，你认为可以讨论抛物线的哪些几何性质？
1.掌握抛物线的范围、对称性、顶点、离心率等几何性质；（重点）2．能根据抛物线的几何性质对抛物线方程进行讨论，在此基础上列表、描点、画抛物线图形；（重点、难点）3．在对抛物线几何性质的讨论中，注意数与形的结合与转化 .
抛物线有许多重要性质.我们根据抛物线的标准方程
研究它的一些简单几何性质.
探究点1 抛物线的简单几何性质
因为p＞0，由方程（1）可知，对于抛物线（1）上的点M (x，y)，x≥0，所以这条抛物线在y轴的右侧，开口方向与x轴正向相同; 当x的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．
以－y代y，方程（1）不变，所以这条抛物线关于x轴对称. 我们把抛物线的对称轴叫做抛物线的轴．
抛物线和它的轴的交点叫做抛物线的顶点.在方程（1）中，当y=0时，x=0，因此抛物线（1）的顶点就是坐标原点．
抛物线上的点M与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示．由抛物线的定义可知，e=1．
过焦点而垂直于对称轴的弦AB，称为抛物线的通径.
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大，抛物线张口越大.
连接抛物线上任意一点与焦点的线段叫做抛物线的焦半径.
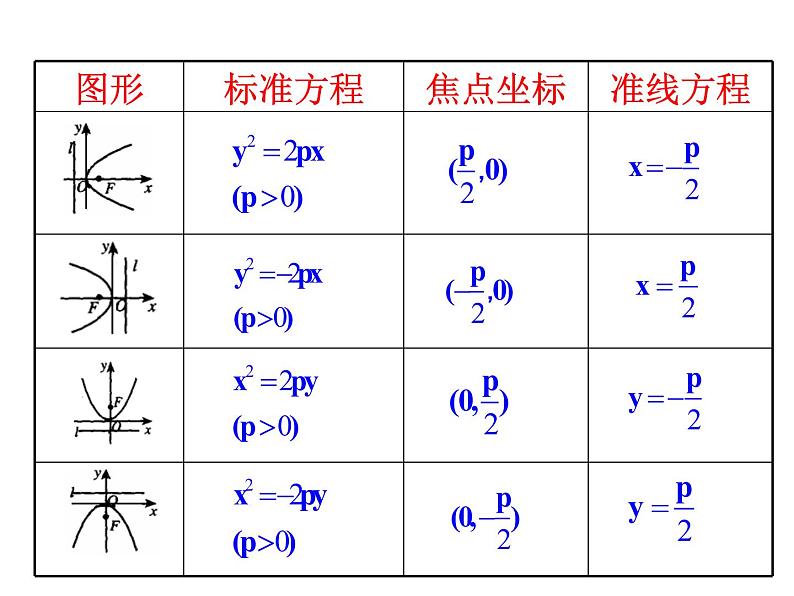
y2 = 2px（p＞0）
y2 = -2px（p＞0）
x2 = 2py（p＞0）
x2 = -2py（p＞0）
(1)抛物线只位于半个坐标平面内，虽然它也可以无限延伸，但没有渐近线；(2)抛物线只有一条对称轴,没有对称中心;(3)抛物线只有一个顶点，一个焦点，一条准线；(4)抛物线的离心率e是确定的，为１;(5)抛物线的通径为2p, 2p越大，抛物线的张口越大.
解：因为抛物线关于x轴对称，它的顶点在坐标原点，并且经过点M（２，　　），所以，可设它的标准方程为
因为点M在抛物线上，所以
因此,所求抛物线的标准方程是
　 【例１】已知抛物线关于x轴对称，它的顶点为坐标原点，并且经过点M（２，　　），求它的标准方程.
分析：由抛物线的方程可以得到它的焦点坐标，又直线l的斜率为1，所以可以求出直线l的方程；与抛物线的方程联立，可以求出A,B两点的坐标；利用两点间的距离公式可以求出∣AB｜.这种方法虽然思路简单，但是需要复杂的代数运算.
下面，我们介绍另外一种方法——数形结合的方法.
还可以如何求x1+x2?
分析：运用抛物线的定义和平面几何知识来证比较简捷．
如上题，求证：以AB为直径的圆和抛物线的准线相切．
所以EH是以AB为直径的圆E的半径，且EH⊥l，因而圆E和准线l相切．
证明：如图，设AB的中点为E，过A，E，B分别向准线l引垂线AD，EH，BC，垂足分别为D，H，C，
则｜AF｜＝｜AD｜，｜BF｜＝｜BC｜
∴｜AB｜＝｜AF｜＋｜BF｜＝｜AD｜＋｜BC｜ =2｜EH｜
4.探照灯反射镜的轴截面是抛物线的一部分，光源位于抛物线的焦点处.已知灯口圆的直径为60 cm，灯深40 cm，建系如图所示，求抛物线的标准方程和焦点位置.
所在平面内建立直角坐标系,使反射镜的顶点与原点重合, x轴垂直于灯口直径.
设抛物线的标准方程为:y2=2px（p＞0），
由条件可得A (40,30),
抛物线只位于半个坐标平面内，虽然它也可以无限延伸，但没有渐近线；
抛物线只有一条对称轴,没有对称中心;
抛物线的离心率是确定的，等于１.
抛物线只有一个顶点，一个焦点，一条准线；