人教版八年级下册17.1 勾股定理教学ppt课件

这是一份人教版八年级下册17.1 勾股定理教学ppt课件，共21页。PPT课件主要包含了勾股定理复习，S1+S2S3，折叠三角形，折叠四边形，数学的世界乐趣无穷等内容，欢迎下载使用。

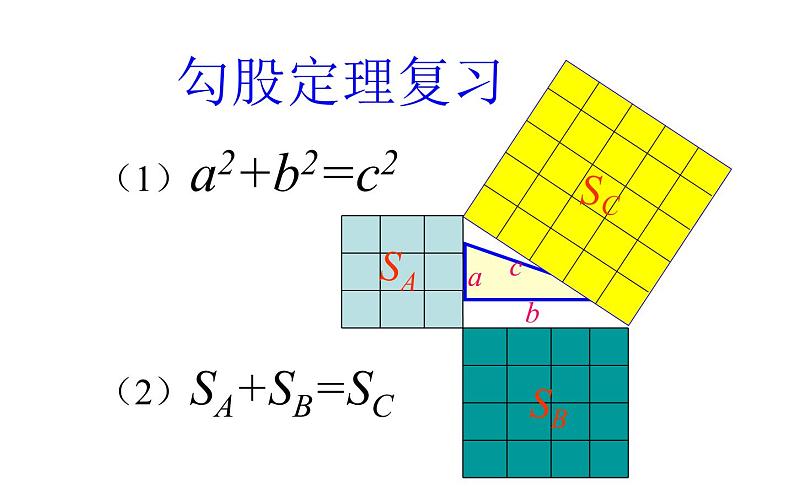
（2）SA+SB=SC
（1）a2+b2=c2
(2)运用勾股定理解决生活中的一些实际问题.
(1)将实际问题转化为数学问题,建立数学模型.
数学源于生活，生活中处处有数学
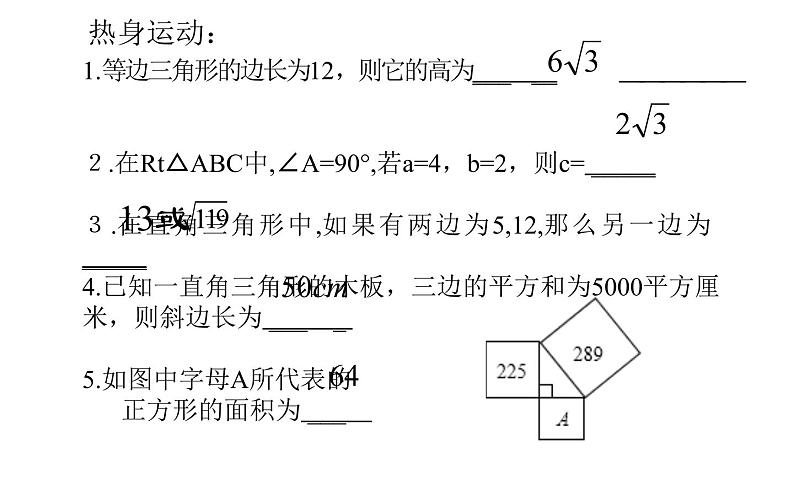
1.等边三角形的边长为12，则它的高为___　__ 　　　　　　　　　　　　２.在Rt△ABC中,∠A=90°,若a=4，b=2，则c= _____ ３.在直角三角形中,如果有两边为5,12,那么另一边为 _____ 4.已知一直角三角形的木板，三边的平方和为5000平方厘米，则斜边长为 ___　_ 5.如图中字母A所代表的 正方形的面积为 ___　
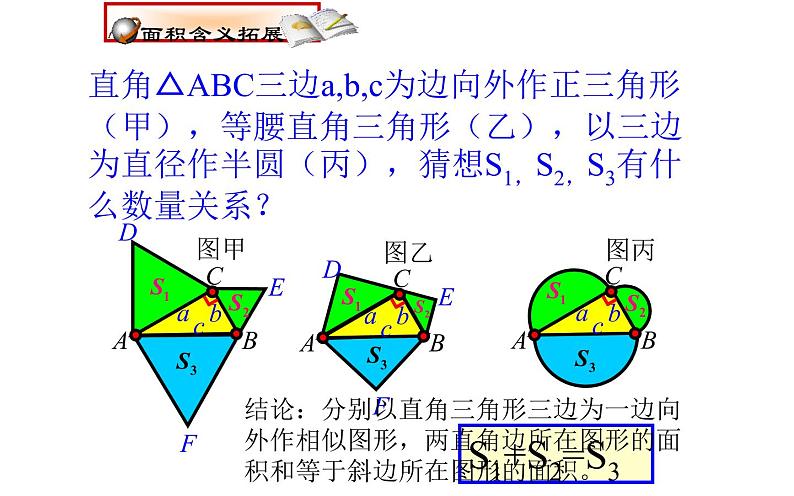
直角△ABC三边a,b,c为边向外作正三角形（甲），等腰直角三角形（乙），以三边为直径作半圆（丙），猜想S1，S2，S3有什么数量关系？
结论：分别以直角三角形三边为一边向外作相似图形，两直角边所在图形的面积和等于斜边所在图形的面积。
巧用勾股定理解折叠问题
原则：翻折的即为全等的方法：方程思想
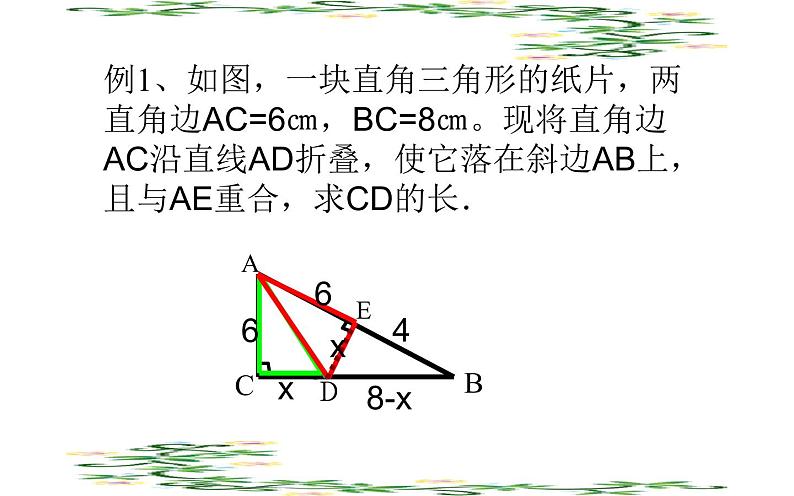
例1、如图，一块直角三角形的纸片，两直角边AC=6㎝，BC=8㎝。现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．
例2、如图，小颍同学折叠一个直角三角形的纸片，使A与B重合，折痕为DE，若已知AC=10cm，BC=6cm,你能求出CE的长吗？
例1：折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求： (1).CF的长 (2).EC的长 (3).折痕AE的长
练习1：折叠矩形纸片，先折出折痕对角线BD，在绕点D折叠，使点A落在BD的E处，折痕DG，若AB=2，BC=1，求AG的长。
巧用勾股定理求 最短距离
-----两点之间线段最短
两点一线（同侧或异侧）
———转化为平面图形来研究
1.如图，在正方体一个顶点A处有一只蚂蚁沿表面向顶点G处爬行，已知正方体的棱长为1，求蚂蚁爬行的最短的距离。
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3）是( ) A.20cm B.10cm C.14cm D.无法确定
如图所示，把枯木看作一个圆柱体，该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处．则问题中葛藤的最短长度是多少尺？
在底面直径为2cm，高为3cm的圆柱体侧面上，用一条无弹性的丝带从A至C按如图所示的圈数缠绕，则丝带的最短长度为　 　cm（结果保留π）
如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为______cm．
如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为______cm．
作业：完成讲义卷（细心、认真）