初中数学人教版八年级下册17.1 勾股定理教学ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理教学ppt课件，共28页。PPT课件主要包含了导入新课，勾股定理的应用，实际问题，数学问题，实物图形，几何图形，新知详解，AB2+BC2，12+22，巩固训练等内容，欢迎下载使用。

如果直角三角形两直角边分别为a、b,斜边为c，那么
即 直角三角形两直角边的平方和等于斜边的平方。
求下列图中表示边的未知数x、y的值。
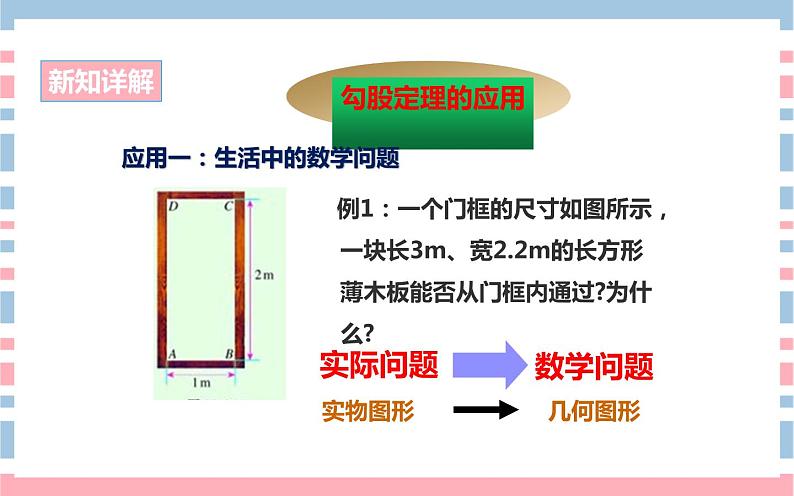
应用一：生活中的数学问题
例1：一个门框的尺寸如图所示，一块长3m、宽2.2m的长方形薄木板能否从门框内通过?为什么?
横着进或竖着进均不可行，因此只能试试斜着。如何确定斜着是否能进去呢？
解：在Rt△ABC中，根据勾股理，AC2=___________=________=_____AC=_____≈______因为______________________________所以木板能从门框内通过。
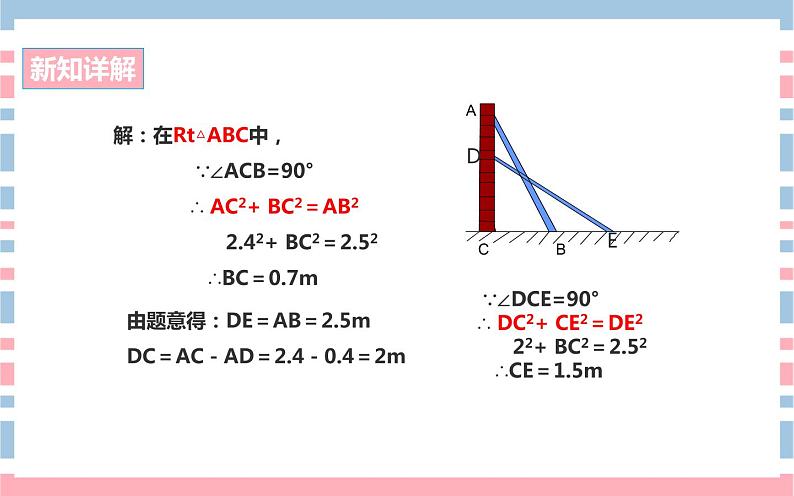
例2：一个2.5m长的梯子AB斜靠在一竖直的墙AC上，这时AC的距离为2.4m．如果梯子顶端A沿墙下滑0.4m，那么梯子底端B也外移0.4m吗？
将问题转化为比较BE与0.4m的大小。
解：在Rt△ABC中， ∵∠ACB=90° ∴ AC2+ BC2＝AB2 2.42+ BC2＝2.52 ∴BC＝0.7m
由题意得：DE＝AB＝2.5mDC＝AC－AD＝2.4－0.4＝2m
∵∠DCE=90° ∴ DC2+ CE2＝DE2 22+ BC2＝2.52 ∴CE＝1.5m
1. 如图，小明家居住的甲楼AB面向正北，现计划在他家居住的楼前修建一座乙楼CD，楼高为18米，已知冬天的太阳最低时，光线与水平线的夹角为30°，若让乙楼的影子刚好不影响甲楼，则两楼之间距离至少应是多少米？
分析：根据CE∥DB，将俯角30°转化到Rt△BCD中，已知CD=18，根据30°的直角三角形的性质可知，CB=2CD，求CB，再利用勾股定理求BD，即为两楼之间距离．
分析：设P、Q同时出发，x秒钟后，AP=xcm，PC=（6-x）cm，CQ=（8-x）cm，利用勾股定理列出方程求解即可．
例3：有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)
长18cm (π的值取3)
求至少要爬多少路程，根据两点之间直线最短，把圆柱体展开，在得到的矩形上连接两点，求出距离即可。
蚂蚁爬行的最短路程是15厘米.
3.如图是一个三级台阶，它的每一级的长、宽、高分别为55寸、10寸和6寸，A和B是这个台阶的两个相对端点，A点上有一只蚂蚁想到B点去吃可口的食物，则它所走的最短路线长度是多少？
解析：展开后得到直角三角形ACB，根据题意求出AC、BC，根据勾股定理求出AB即可。
立体问题要巧妙的展开图形。
例4:矩形ABCD如图折叠，使点D落在BC边上的点F处，已知AB=8，BC=10，求折痕AE的长。
则CE为 (8- x).
由题意可知:EF=DE=x,
∵∠B=90° ∴ AB2+ BF2＝AF2
82+ BF2＝102 ∴BF＝6
∴CF＝BC－BF＝10－6＝4
∵∠C=90° ∴ CE2+CF2＝EF2
(8－ x)2+42=x2
利用勾股定理解决实际问题的一般思路： （1）重视对实际问题正确理解； （2）建立对应的数学模型运用相应的数学知识；　（3）方程思想在本题中的运用
4.如图，把长方形ABCD沿FE折叠，使点B落在边AD上的点B′处，点A落在点A′处，若AE=3，BF=4，则AB长是多少？。
分析：由折叠的性质知：BF=B′F，且∠B′FE=∠BFE，由AD∥BC可知∠B′EF=∠BFE，通过等量代换可证得B′E=B′F=BF，进而可在Rt△A′B′E中，利用勾股定理得到所求线段与已知线段间的数量关系。
1.已矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿线段DA、线段BA向点A的方向运动，当动点M运动到点A时，M、N两点同时停止运动．连接FM、FN．设点M、N的运动速度都是1个单位/秒，M、N运动的时间为x秒，问：当x为多少时，FM⊥FN？
分析：首先构造直角三角形，用x表示出各部分的长度，再结合勾股定理求出x的值