




数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆优质课件ppt
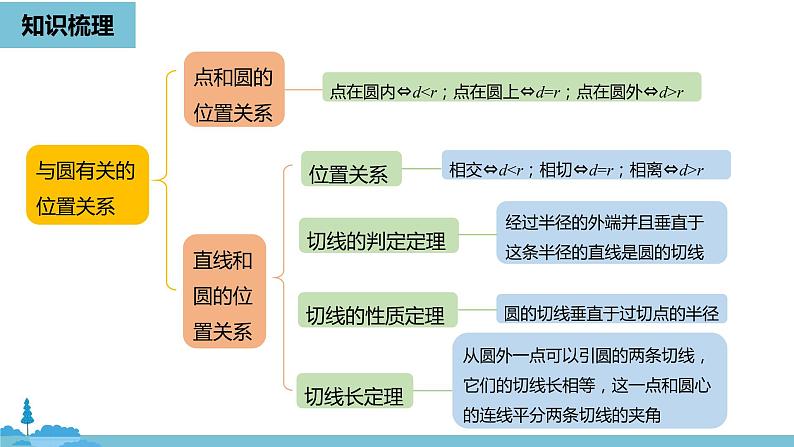
展开点在圆内⇔d
相交⇔d
经过半径的外端并且垂直于这条半径的直线是圆的切线
圆的切线垂直于过切点的半径
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角
有关概念:正多边形的中心、半径、中心角、边心距
尺规作图法作圆的内接正多边形
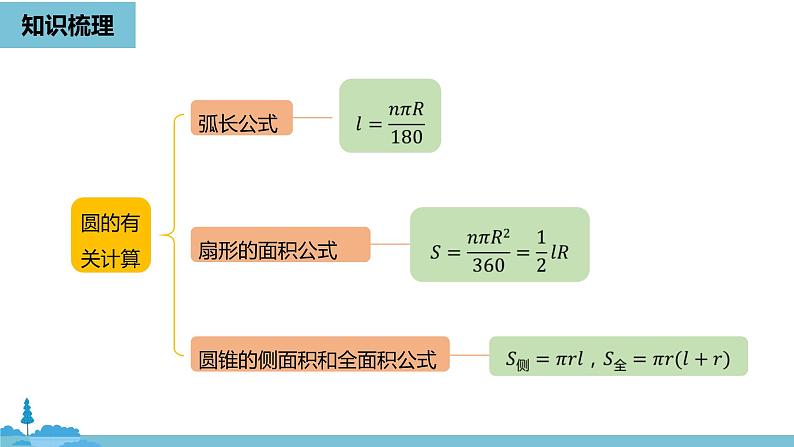
圆锥的侧面积和全面积公式
1.中心:正多边形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
2.半径:外接圆的半径叫做正多边形的半径.
3.边心距:中心到正多边形一边的距离叫做正多边形的边心距.
4.中心角:正多边形每一条边所对的外接圆的圆心角都相等,叫做正多边形的中心角.
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.设☉O的半径是r,点P到圆心的距离为d,则有
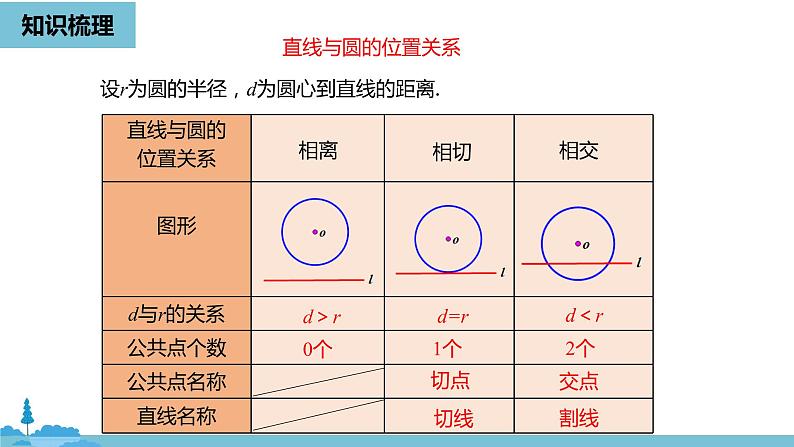
设r为圆的半径,d为圆心到直线的距离.
1.判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
2.性质定理:圆的切线垂直于经过切点的半径.
3.切线长定理:经过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
弓形的面积=扇形的面积±三角形的面积
3.圆锥的侧面积为πrl.
4.圆锥的全面积为πrl+πr2.
1.圆锥的侧面展开图是一个扇形.2.如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr.
如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.(1) 求证:CD与☉O相切.(2) 若正方形ABCD的边长为1,求☉O的半径.
(1) 证明:过点O作ON⊥CD于N.连接OM, ∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.∴AC是∠BCD的平分线,∴ON=OM,∴CD与☉O相切.
如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.(1) 求证:CD与☉O相切;(2) 若正方形ABCD的边长为1,求☉O的半径.
解:(2)∵⊙O分别切PA,PB,DE于A,B,C,∴AD=CD,BE=CE.∴ △PDE的周长=PD+PE+DE=PD+AD+BE+PE=2PA=8(cm).
如图,四边形OABC为菱形,点B,C在以点O为圆心的圆上,OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合, 点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
如何作圆内接正五边形?
解:作法不唯一,如:(1) 用量角器作72°的中心角,得圆的五等分点;(2) 依次连接各等分点,得圆的内接正五边形.
☉O的半径为R,圆心到点A的距离为d,且R,d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )A. 点A在☉O内部 B. 点A在☉O上C. 点A在☉O外部 D. 点A不在☉O上
解:解方程 x2-6x+8=0的两根,得R=2,d=4,或R=4,d=2,当R=2,d=4时,点A在⊙O外部;当R=4,d=2时,点A在⊙O内部;综上所述,点A不在⊙O上.
如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1 cm的☉P的圆心在射线OA上,且与点O的距离为6 cm,如果☉P以1 cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
解:当⊙P在射线OA上,设⊙P与CD相切于点E,P移动到P1时,连接P1E.∵⊙P与直线CD相切,∴∠OEP1=90°,∵在直角△OP1E中,P1E=1cm,∠AOD=30°,∴OP1=2P1E=2cm,则PP1=OP-OP1=6-2=4(cm),
∵⊙P以1 cm/s的速度沿由A向B的方向移动,∴⊙P移动4秒时与直线CD相切.当⊙P移动到直线CD的右侧时,PP2=4+4=8(cm).∴⊙P移动8秒时与直线CD相切.综上,⊙P移动4秒或8秒时,与直线CD相切.
一条弧所对的圆心角为135 ° ,弧长等于半径为5 cm的圆的周长的3倍,则这条弧的半径为 .
若一个正六边形的周长为24,则该正六边形的面积为______.
如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_____.
如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.(1) 求正方形EFGH的面积;(2) 连接OF,OG,求∠OGF的度数.
解:(1) ∵正六边形的边长与其半径相等,∴EF=OF=5.∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH的面积是25.
初中数学人教版九年级上册24.1.1 圆教学演示ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c88761_t3/?tag_id=26" target="_blank">24.1.1 圆教学演示ppt课件</a>,文件包含244第2课时圆锥的侧面积和全面积pptx、2442mp4等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
初中数学人教版九年级上册24.1.1 圆完美版课件ppt: 这是一份初中数学人教版九年级上册24.1.1 圆完美版课件ppt,共20页。PPT课件主要包含了图中都有圆,与圆有关的概念,同步练习,谈谈你有什么收获等内容,欢迎下载使用。
初中第二十四章 圆24.1 圆的有关性质24.1.1 圆图片ppt课件: 这是一份初中<a href="/sx/tb_c88761_t3/?tag_id=26" target="_blank">第二十四章 圆24.1 圆的有关性质24.1.1 圆图片ppt课件</a>,共25页。PPT课件主要包含了圆的有关概念,知识精讲,旋转定义,集合定义,同圆半径相等,有关概念,弦直径,直径是圆中最长的弦,半圆是特殊的弧,同心圆等内容,欢迎下载使用。













