初中数学北师大版九年级下册5 确定圆的条件优秀ppt课件

这是一份初中数学北师大版九年级下册5 确定圆的条件优秀ppt课件，共12页。PPT课件主要包含了课题确定圆的条件，议一议，巩固训练，课堂小结等内容，欢迎下载使用。

某地区在一空地上新建了三个居住小区A、B、C,现要规划一间学校，使学校到三个小区的距离相等。你如何选取这所学校的地点？
1、当A、B、C三点在同一直线时怎样？
2、当A、B、C三点不在同一直线时怎样？
类比确定直线的条件:
1、经过一点可以作无数条直线
2、经过两点只能作一条直线
3、经过三点能作几条直线？
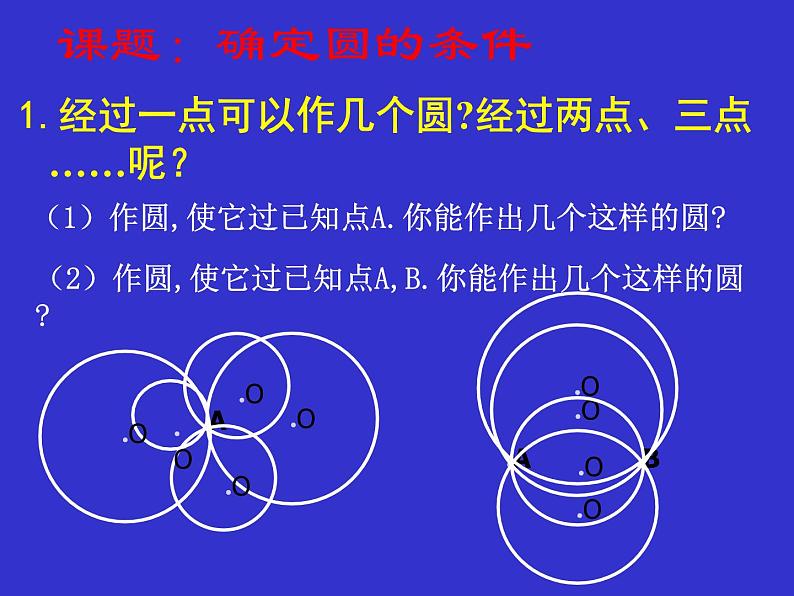
1.经过一点可以作几个圆?经过两点、三点……呢？
（1）作圆,使它过已知点A.你能作出几个这样的圆?
（2）作圆,使它过已知点A,B.你能作出几个这样的圆?
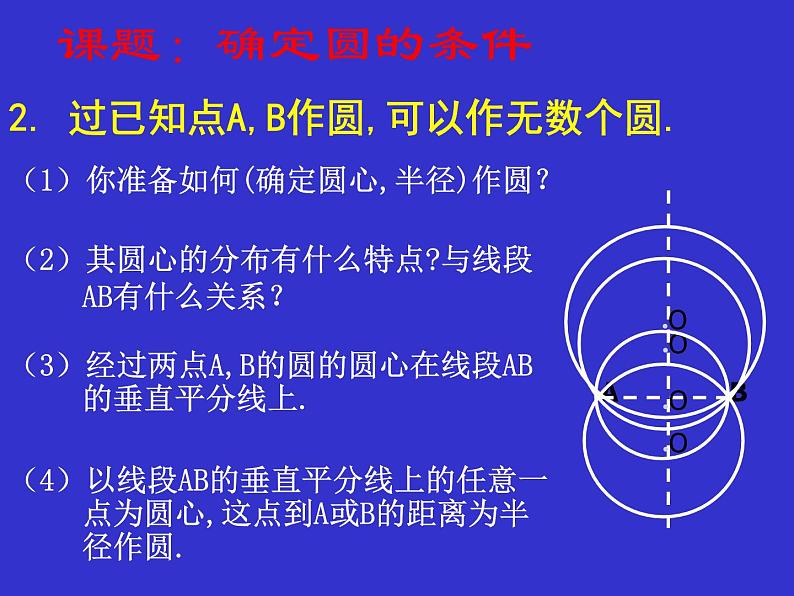
2. 过已知点A,B作圆,可以作无数个圆.
（1）你准备如何(确定圆心,半径)作圆？
（2）其圆心的分布有什么特点?与线段 AB有什么关系？
（3）经过两点A,B的圆的圆心在线段AB的垂直平分线上.（4）以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
3.作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上),你能作出几个这样的圆?
老师提示:1、能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上.
（2）其圆心的位置有什么特点?与A,B,C有什么关系？
2、经过两点B,C的圆的圆心在线段BC的垂直平分线上.
3、经过三点A,B,C的圆的圆心应该这两条垂直平分线的交点O的位置.
定理 ：不在同一条直线上的三个点确定一个圆.
1、三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.
2、外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
如果三个点在同一直线时可以作圆吗？为什么？
1、分别作出锐角三角形、直角三角形、钝角三角形的外接圆,并说明它们外心的位置情况。
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
2、判断题：①经过三点一定可以作圆 （ ）②任意一个三角形有且只有一个外接圆（ ）③三角形的外心是三角形三边中线的交点（ ）④三角形外心到三角形三个顶点距离相等（ ）
3、如图是一块残缺的圆形木盖，现要重新制 作一块与原来一样大小的圆形木盖，你是 如何制作的？
4、你现在能解决课前的问题了吗？
1、通过本课的学习，你有什么收获？还有什么问题？
2、确定圆的条件——
3、锐角三角形 在三角形的内部 直角三角形 --外心的位置--- 在斜边上 钝角三角形 在三角形的外部